Hypotetiska HP frågor: miniaturhäst tävling
En miniaturhäst tävling* mellan Ann-Britt den Blodig Slipmakin och Ylva den Rostig Borrare genomfördes på en bana som man åkte två varv. Vem hade bästa tiden av de två ryttarna mellan Ann-Britt den Blodig Slipmakin och Ylva den Rostig Borrare?
1. Slipmaskinen startade kl 09:56 och Borraren kl 10:52. Borraren passerade mållinjen precis 55 minuter senare än Slipmaskinen.
2. Slipmaskinen behövde 38 minuter för att åka det första varvet och 2 minuter längre tid för att åka det andra. Borraren åkte den andra varvet lika fort som det första.
Jag har ingen aning om det är möjligt att avgöra tiderna för båda barbarerna. Kan detta lösas?
(*!!Ryttare åkte utan rustning och inga miniaturhäst blev skadad under tävling!!)
Viktigt här är att notera att du egentligen inte behöver avgöra vilka tider ryttarna behövde för att ta sig runt banan, utan endast vilken tid som är kortast.
1. S startar 09:56. En timme senare är klockan 10:56. Fyra minuter innan dess, 10:52, startade B. 1 h - 4 min = 56 min. B passerade mållinjen 55 minuter senare än S. Oavsett hur lång tid de tog på sig måste B ha varit snabbare, eftersom B:s tid var en minut kortare än S.
2. B kan ha åkt sina varv med (nästan) ljusets hastighet, eller lunkat fram långsamt. Vi kan alltså inte säga något om den totala tiden här.
Svar: i (1) men ej i (2). Dvs. B ...?
1. Borraren startade 56 minuter efter Slipmaskinen och gick i mål 55 minuter efter. Vem hade snabbast tid?
2. Slipmaskinen behöver 78 minuter för båda varven. Vi vet inte hur lång tid det tar för Borraren (vi kan räkna ut den om vi kombinerar med påstående 1).
Genom påstående 1 kan vi avgöra vem som har bäst tid, men inte beräkna tiden. Genom påstående 2 kan vi beräkna den ena tiden, men inte veta vem som vinner.
Hmm men även om Borraren startade 56 minuter efter Slippmaskinen, det står ingenstans att Slippmaskinen var inte klar efter 20, 36 eller 56 minuter, eller?
I påstående 2 står det att första varvet tog 38 minuter och andra varvet tog 40 minuter för Slipmaskinen - men det spelar ingen roll för att svara på frågan.
Korrekt, men vi vet skillnaden mellan de två tiderna. Om Slipmaskinen tog 5 minuter för att gå i mål, måste Borraren ha klarat loppet på 4 minuter för att kunna gå i mål 55 minuter senare. Oavsett tider måste B vara en minut snabbare än S.
Edit: Skillnad, inte förhållande. Dumstruten är på idag, alltså.
Smutstvätt skrev :Korrekt, men vi vet förhållandet mellan de två tiderna. Om Slipmaskinen tog 5 minuter för att gå i mål, måste Borraren ha klarat loppet på 4 minuter för att kunna gå i mål 55 minuter senare. Oavsett tider måste B vara en minut snabbare än S.
Nej, vi vet inte förhållandet, men vi vet skillnaden. Förhållande har med division att göra, skillnad med subtraktion.
Smaragdalena skrev :Smutstvätt skrev :Korrekt, men vi vet förhållandet mellan de två tiderna. Om Slipmaskinen tog 5 minuter för att gå i mål, måste Borraren ha klarat loppet på 4 minuter för att kunna gå i mål 55 minuter senare. Oavsett tider måste B vara en minut snabbare än S.
Nej, vi vet inte förhållandet, men vi vet skillnaden. Förhållande har med division att göra, skillnad med subtraktion.
Jag är kass idag, alltså. :S Tack för påminnelsen!
Hmmm ok... Borraren åker 56 minuter efter Slippis och är i målet 55 minuter efter henne. Hon har vunnit en minut.
(varför har jag så svårt att fatta grrr)
Ja, precis! Tänk dig sträckor istället, så blir det lättare att visualisera:
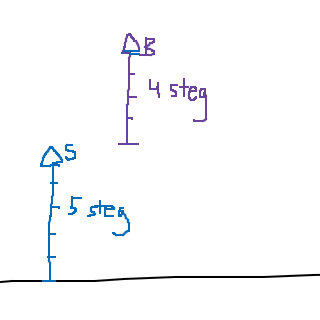
B börjar längre fram på banan, men går endast fyra steg, medan S börjar längre bak, men går fem steg. Trots att B är längre fram på banan, har S gått flest steg.
Jag det blev mycket klarare, hoppas att det hänger kvar till HP.

Nästa HP:






