Hyperbol och grafer

Meow123 skrev:

Hej!

 

Hur kan jag veta hur denna graf ser ut? 

Hyperbolens definition är ju x^2/a^2 - y^2/b^2 = -1, jag hittar absolut inget samband.

 

Jag har löst ut y^2

får då y^2 = sqrt(x^2+1) och jag vet att absolut beloppfunktionen definieras som sqrt(x^2) så jag tänker att vi får två funktioner:

y1 = sqrt(x^2+1) och y2 = -sqrt(x^2+1) vilket är absolutbelopp - funktionen men shiftad och speglad i X-led.

 

Det känns långsökt och fel, finns det ett bättre sätt?
Tack!

Sätt a = b = 1 i definitionen av hyperbolen och jämför med ditt uttryck.

Smaragdalena skrev:

Meow123 skrev:

Hej!

 

Hur kan jag veta hur denna graf ser ut? 

Hyperbolens definition är ju x^2/a^2 - y^2/b^2 = -1, jag hittar absolut inget samband.

 

Jag har löst ut y^2

får då y^2 = sqrt(x^2+1) och jag vet att absolut beloppfunktionen definieras som sqrt(x^2) så jag tänker att vi får två funktioner:

y1 = sqrt(x^2+1) och y2 = -sqrt(x^2+1) vilket är absolutbelopp - funktionen men shiftad och speglad i X-led.

 

Det känns långsökt och fel, finns det ett bättre sätt?
Tack!

Sätt a = b = 1 i definitionen av hyperbolen och jämför med ditt uttryck.

Hej, jag skrev fel, det ska vara 1 

Om man byter plats på x och y i

x²-y² = 1

så får man

x²-y² = -1

så båda är hyperblar.

Laguna skrev:

Om man byter plats på x och y i

x²-y² = 1

så får man

x²-y² = -1

så båda är hyperblar.

hur menar du, jag hänger inte riktigt med

Laguna skrev:

Om man byter plats på x och y i

x²-y² = 1

så får man

x²-y² = -1

så båda är hyperblar.

Det skall nog vara att x²-y² = 1 är samma sak som y²-x² = -1. Sedan kan man byta namn på x till y och y til x, så får man x²-y² = -1.

Smaragdalena skrev:

Laguna skrev:

Om man byter plats på x och y i

x²-y² = 1

så får man

x²-y² = -1

så båda är hyperblar.

Det skall nog vara att x²-y² = 1 är samma sak som y²-x² = -1. Sedan kan man byta namn på x till y och y til x, så får man x²-y² = -1.

Jaha okej, om man byter plats på variablerna kommer hyperbolen att vara vriden, typ att y-axeln blir den nya x-axeln vilket förklarar dens utseende?

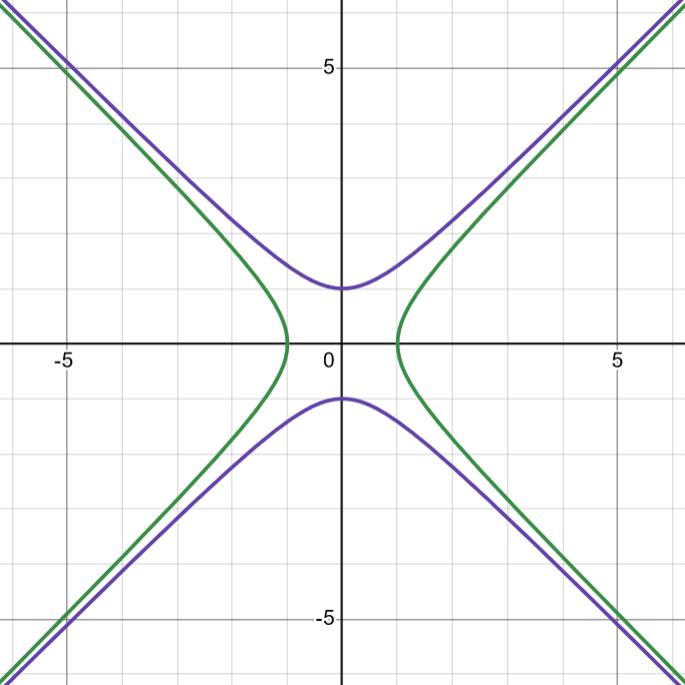
x²-y² = 1 är grön. x²-y² = -1 (samma sak som y²-x² = 1) är blålila.

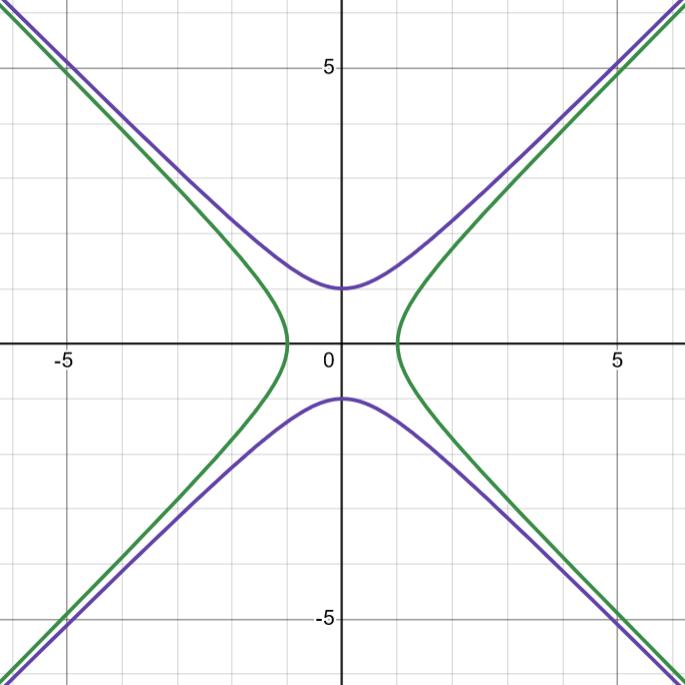
Smaragdalena skrev:

x²-y² = 1 är grön. x²-y² = -1 (samma sak som y²-x² = 1) är blålila.

Jaha okej! Misstänkte det men hur kan man förklara vad som händer med en graf när man ”byter plats” på variablerna? Tack!

Pröva att rita själv, för hand. Om du behöver mer ledning: Lägg upp din halvfärdiga bild här och fråga igen.

Smaragdalena skrev:

Pröva att rita själv, för hand. Om du behöver mer ledning: Lägg upp din halvfärdiga bild här och fråga igen.

Okej jag ska testa men vilken graf ska jag ska rita?

x²-y² = 1 till att börja med. Rita i intervallet -5 < x < 5.

Smaragdalena skrev:

x²-y² = 1 till att börja med. Rita i intervallet -5 < x < 5.

Sådär, och sedan byter jag plats på variablerna och då kommer y-axeln att ”bli” den nya x-axeln vilket förklarar nr 48s ekvation ?

Pröva att rita upp dels så som den är skriven, dels skriven som y²-x² = 1. Du kommer att se att det blir precis samma punkter.