Hur vet man om det är en terasspunkt?
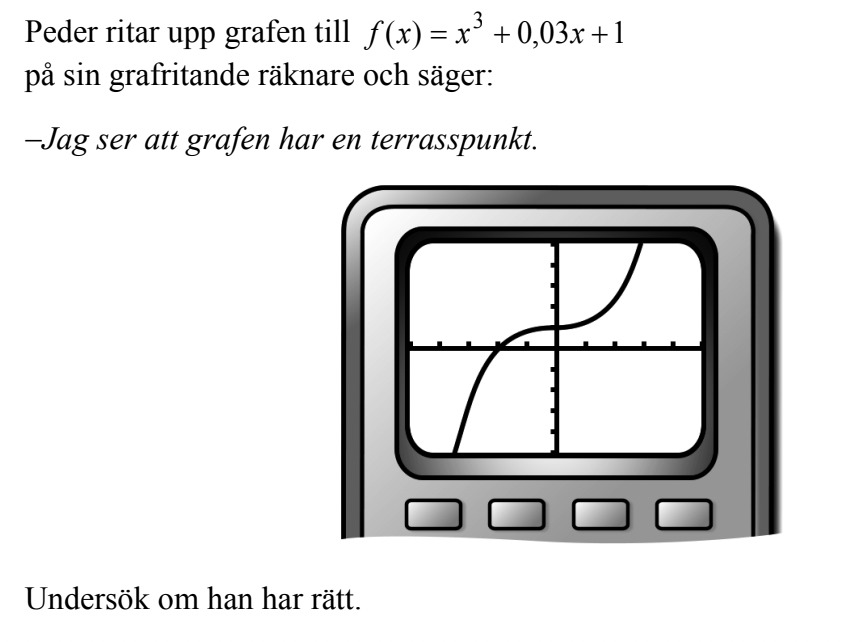Jag har ritat upp grafen samt derivatan och gjort f'(x)=0 men får ingen lösning. Kollar jag på derivatan så når den aldrig noll heller. Vad jag inte förstår är varför måste f'(x)=0 för att det ska vara en terasspunkt.
Ett gemensamt namn för minimi-, maximi- och terrasspunkter är stationära punkter.
Det som kännetecknar en stationär punkt är att derivatan i den punkten alltid är lika med 0.
Så om du har en funktion vars derivata saknar (reella) nollställen så kan du alltså säga att den funktionen saknar stationära punkter.
Alltså har den vare sig minimi-, maximi- eller terrasspunkter.
Fick du även svar på din fråga om varför det måste gälla att f'(x) = 0 vud en terrasspynjt då?
Yngve skrev:Ett gemensamt namn för minimi-, maximi- och terrasspunkter är stationära punkter.
Det som kännetecknar en stationär punkt är att derivatan i den punkten alltid är lika med 0.
Så om du har en funktion vars derivata saknar (reella) nollställen så kan du alltså säga att den funktionen saknar stationära punkter.
Alltså har den vare sig minimi-, maximi- eller terrasspunkter.
Fick du även svar på din fråga om varför det måste gälla att f'(x) = 0 vud en terrasspynjt då?
Ja nu förstår jag. Tack!
