Hur stor ska dragkraften vara för att få lådorna att agera som ett objekt. Tänker jag rätt?

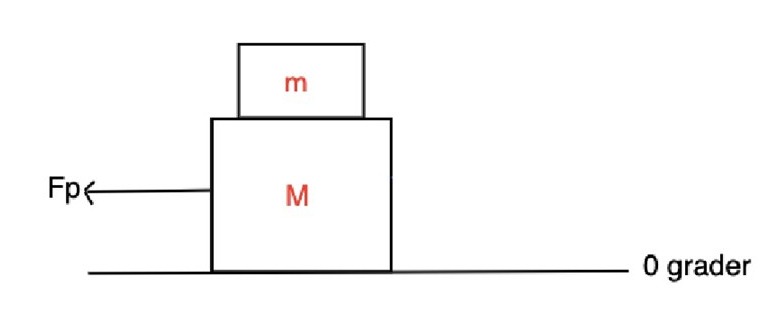
Given information är att friktionskonstanten är $μ$ på kontaktytorna. Massan på lådorna är m för den lilla lådan och M för den stora lådan.

Q1: Hur stor kan kraften Fp vara om både lådorna ska röra sig som om de vore vara en enda kropp?

Lösning:

Newtons andra lag säger att: F = m*a, med detta kan vi säga att Fp = total massan * accelerationen:

Fp = (m+M)a

För att räkna accelerationen a, används newtons andra lag på nytt men med avseende på friktionskraften som verkar mellan lådorna och som stoppar låda m från att glida, denna friktionskraft kallar jag för Fm. Friktionskraften Fm kan räknas med formeln, Fm = μmg.

Fm = ma <-> (newtons andra lag tillämpas) <-> μmg = ma -> a = μg

Detta ger att accelerationen a = μg för att få lådorna att röra sig som en kropp. a kan nu sättas i Fp = (m+M)a:

Fp = (m+M)a -> Fp = (m+M)*μg

Svar: Fp kan vara (m+M)*μg stort så att båda lådorna rör sig som en kropp då undre lådan M dras.

Fp = (m+M)*μg

Q2: Beräkna lådornas acceleration om dragkraften Fp som krävs för att båda lådorna ska röra sig som en kropp fördubblas: det vill säga att Fp -> 2Fp:

Lösning:

Utför samma procedur som innan men nu är dragkraften dubbelt så stor:

2Fp = 2*(total massan * accelerationen) = 2(M+m)*a

2Fp = / a=μg /= 2(M+m)*μg

Accelerationen för den lilla lådan räknas med hjälp av friktion sambandet på den lilla lådan som innan, Fm = μmg:

Fm = ma <-> (newtons andra lag tillämpas) <-> μmg = ma -> a = μg

* Accelerationen på den lilla lådan m är : a = μg

Accelerationen för den stora lådan räknas genom att räkna den totala kraften Ftot som verkar på lådan: Krafterna som verkar på den stora lådan M är dragkraften 2Fp och en friktionskraft Fm+M = (M+m)*μg:

Ftot = 2Fp - Fm+M = 2(M+m)*μg - (M+m)*μg = (M+m)*μg

Newtons andra lag F = ma ger att:

Ftot => (M+m)*μg = m * a => a = $\frac{(M + m) * μ g}{m}$

* Acceleration på den stora lådan: a = $\frac{(M + m) * μ g}{m}$

Stämmer min tankeprocedur och lösning? Tack på förhand och sorry för det långa inlägget!

Q1: Håller med.

Q2:
Det där verkar lite skumt. Fm är en kraft som adderas med en massa?

Kom att tänka på en sak till:
Man kanske också ska ta med friktionen mellan den stora lådan och marken. Är den kanske samma som mellan lådorna?

Q1: Lådorna börjar röra sig (med oändligt liten acceleration) när friktionsvillkoret för fullt utvecklad statisk friktion är uppfyllt. Det inträffar mycket riktigt då $F_p=(m+M)\mu g$ , men det är inte sant att $a=\mu g$ .

Hej Thomas, jag hade en dålig beteckning på friktionskraften, den ska egentligen vara på följande sätt: $F_{M + m}$ , Denna friktionskraft är friktionen mellan den stora lådan och marken som du påpekade, jag tänkte dock att friktionskraften kommer att bero på båda lådornas massor (m+M) eftersom övre lådan gör att massan som undre lådan utövar på marken är större vilket resulterar i mer friktion tänker jag. Sen använder jag friktions formeln (F = mμg) och detta ger att friktionskraften mellan marken och stora lådan (båda lådornas vikt) blir:

$F_{M + m} = (M + m) *$ μg

Hej D4NIEL, varför tycker du att $a = μ g$ inte stämmer?

Accelerationen "stämmer", men jag tycker inte det framgår av din redovisning hur du kommit fram till den. Jag kanske missförstår vad du menar, men för paketet gäller att

$F_p-F_f=(M+m)a$ <--- Den här ekvationen saknar jag i din redovisning.

$F_f=\mu (M+m)g$ (fullt utvecklad friktion mot golvet för paketet (M+m))

Detta ger ett annat uttryck för $F_p$ .

Den övre klossen börjar glida när accelerationen av den övre massan kräver en kraft som överstiger fullt utvecklad friktion dvs $\mu m g$ .

Svara

Visa senaste svar