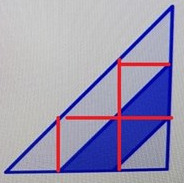
Hur stor del av triangelns area är markerad?
Asså vet inte ens hur jag ska börja med med denna uppgiften. Det jag bara vet att triangelns area är b*h/2
Du kan göra på olika sätt.
Ett sätt är att se att det finns tre rätvinkliga trianglar T1, T2 och T3.
Om du sätter basen (och höjden) på den största triangeln T1 till 1 så kan du beräkna dess area A1
Basen och höjden på den mindre triangeln T2 är då 2/3. Då kan du beräkna dess area A2.
Basen och höjden på den minsta triangeln T3 ät då 1/3. Dess area kallar vi A3.
Det blåa området har nu arean A2-A3.
Kommer du vidare med den metoden?
Yngve skrev:Du kan göra på olika sätt.
Ett sätt är att se att det finns tre rätvinkliga trianglar T1, T2 och T3.
Om du sätter basen (och höjden) på den största triangeln T1 till 1 så kan du beräkna dess area A1
Basen och höjden på den mindre triangeln T2 är då 2/3. Då kan du beräkna dess area A2.
Basen och höjden på den minsta triangeln T3 ät då 1/3. Dess area kallar vi A3.
Det blåa området har nu arean A2-A3.
Kommer du vidare med den metoden?
nej jag förstår inte ens hur du menar
Så här:



Yngve skrev:Så här:
Vad menar du med T2 och T3? Kan man göra ett utryck för att få svaret?
T1, T2 och T3 är namn på de tre trianglarna (som vi använder för att ange vilka trianglar vi talar om).
Yngve har skrivit in bas och höjd för varje triangel.
Använd b*h/2 för att räkna ut varje triangels area.
Om du tycker att det blir enklare kan du i stället säga att T3 har bas och höjd = 1,
T2 bas och höjd = 2 och T1 bas och höjd = 3.
Louis skrev:T1, T2 och T3 är namn på de tre trianglarna (som vi använder för att ange vilka trianglar vi talar om).
Yngve har skrivit in bas och höjd för varje triangel.
Använd b*h/2 för att räkna ut varje triangels area.Om du tycker att det blir enklare kan du i stället säga att T3 har bas och höjd = 1,
T2 bas och höjd = 2 och T1 bas och höjd = 3.
 Hur tänker de här?
Hur tänker de här?
ghada.alamer skrev:
Vad menar du med T2 och T3? Kan man göra ett utryck för att få svaret?
Ja, det går att skriva ett uttryck för svaret, men det bästa är om du kommer fram till det på egen hand.
Vilket/vilka av följande påståenden är du inte med på?
- T1 är den stora triangeln markerad i rött i första bilden.
- T1 har basen 1, höjden 1 och alltså arean A1 = b*h/2 = 1*1/2 = 1/2 a.e.
- T2 är den mellanstora triangeln markerad i rött i andra bilden.
- T2 har basen 2/3, höjden 2/3 och alltså arean A2 =(2/3)*(2/3)/2 = (4/9)/2 = 2/9 a.e.
- T3 är den minsta triangeln markerad i rött i tredje bilden.
- T3 har basen 1/3, höjden 1/3 och allså arean A3 = (1/3)*(1/3)/2 = (1/9)/2 = 1/18 a.e.
- Det blåa fältet i bilden har arean A2-A3 = 2/9-1/18 = 4/18-1/18 = 3/18 a.e.
Kan du nu ta fram ett uttryck för hur stor andel av den stora trianelns area som det blåa fältet utgör?
Yngve skrev:ghada.alamer skrev:
Vad menar du med T2 och T3? Kan man göra ett utryck för att få svaret?Ja, det går att skriva ett uttryck för svaret, men det bästa är om du kommer fram till det på egen hand.
Vilket/vilka av följande påståenden är du inte med på?
- T1 är den stora triangeln markerad i rött i första bilden.
- T1 har basen 1, höjden 1 och alltså arean A1 = b*h/2 = 1*1/2 = 1/2 a.e.
- T2 är den mellanstora triangeln markerad i rött i andra bilden.
- T2 har basen 2/3, höjden 2/3 och alltså arean A2 =(2/3)*(2/3)/2 = (4/9)/2 = 2/9 a.e.
- T3 är den minsta triangeln markerad i rött i tredje bilden.
- T3 har basen 1/3, höjden 1/3 och allså arean A3 = (1/3)*(1/3)/2 = (1/9)/2 = 1/18 a.e.
- Det blåa fältet i bilden har arean A2-A3 = 2/9-1/18 = 4/18-1/18 = 3/18 a.e.
Kan du nu ta fram ett uttryck för hur stor andel av den stora trianelns area som det blåa fältet utgör?
ska jag subtrahera 3/18-2/9? och hur kom du fram till att mellanstora triangeln har höjden 2/3?
Nej, andel innebär division.
Exempel (med påhittade siffror):
Om a = 3 och b = 5 och vi vill veta hur stor andel a är av b så ska vi dividera a med b. Andelen blir då a/b, dvs 3/5.
======
Svar på frågan om höjden på den mellanstora triangeln: Det står i uppgiften att de två sidorna är uppdelade i tre lika stora delar. Varje sådan del är 1/3 l.e.
Mellantriangelns höjd består av två sådana tredjedelar, alltså 2*1/3 = 2/3.
Yngve skrev:Nej, andel innebär division.
Exempel (med påhittade siffror):
Om a = 3 och b = 5 och vi vill veta hur stor andel a är av b så ska vi dividera a med b. Andelen blir då a/b, dvs 3/5.
======
Svar på frågan om höjden på den mellanstora triangeln: Det står i uppgiften att de två sidorna är uppdelade i tre lika stora delar. Varje sådan del är 1/3 l.e.
Mellantriangelns höjd består av två sådana tredjedelar, alltså 2*1/3 = 2/3.
Blir det 3/2
3/2=1,5. Vi ser på bilden att det måste vara mindre än 1 eftersom det endast är en del av triangeln som är markerad. Skulle hela triangeln vara markerad skulle svaret vara 1. Bara om markeringen är större än triangeln kan vi få värden som är större än 1.
ghada.alamer skrev:
Blir det 3/2
Nej. Om du visar hur du räknar så kan vi hjälpa dig att hitta feltänket/felräkningen.
Ett annat sätt är att dela in den stora triangeln i små trianglar, som är lika stora som den lilla vita triangeln: Hur många trianglar är det totalt? Hur många av trianglarna är blå?
Om vi samlar på olika sätt är ytterligare ett att använda likformigheten
och att areaskalan är kvadraten på längdskalan.
Om den minsta triangeln har arean A har den näst största arean 4A och den största arean 9A.
Det sökta förhållandet är (4A-A)/9A = 3A/9A = 1/3.
Men Smaragdalenas sätt är väl det enklaste.
Yngve skrev:Nej, andel innebär division.
Exempel (med påhittade siffror):
Om a = 3 och b = 5 och vi vill veta hur stor andel a är av b så ska vi dividera a med b. Andelen blir då a/b, dvs 3/5.
======
Svar på frågan om höjden på den mellanstora triangeln: Det står i uppgiften att de två sidorna är uppdelade i tre lika stora delar. Varje sådan del är 1/3 l.e.
Mellantriangelns höjd består av två sådana tredjedelar, alltså 2*1/3 = 2/3.
du gav ju ett exempel här och gjorde samma sak.
Yngve skrev:ghada.alamer skrev:Blir det 3/2
Nej. Om du visar hur du räknar så kan vi hjälpa dig att hitta feltänket/felräkningen.
Som sagt finns det tre rätvinkliga trianglar: T1, T2 och T3.
T1 den stora trianglen har basen 1 och höjden 1 och är arean alltså At=b*h/2=1*1/2=1/2.
T2 den mellanstora trianglen och har besen 2/3, höjden 2/3 och är arean alltså arean A2=(2/3)*(2/3)/2=2/9.
T3 den minsta triangel med basen 1/3 och höjden 1/3 och arean är A3= (1/3)*(1/3)/2=(1/9)/2.=1/18
Den blå fältet har arean A2-A3=2/9-1/18=3/18.
Men jag kommer inte vidare!
Smaragdalena skrev:Ett annat sätt är att dela in den stora triangeln i små trianglar, som är lika stora som den lilla vita triangeln: Hur många trianglar är det totalt? Hur många av trianglarna är blå?
1/3
Den blå fältet har arean A2-A3=2/9-1/18=3/18
som är lika med 1/6.
T1 den stora trianglen har basen 1 och höjden 1 och är arean alltså At=b*h/2=1*1/2=1/2.
Och de frågar efter hur stor del av den stora triangeln (area 1/2) som är blåmarkerad (area 1/6).
Louis skrev:Den blå fältet har arean A2-A3=2/9-1/18=3/18
som är lika med 1/6.
T1 den stora trianglen har basen 1 och höjden 1 och är arean alltså At=b*h/2=1*1/2=1/2.
Och de frågar efter hur stor del av den stora triangeln (area 1/2) som är blåmarkerad (area 1/6).
Ehm ska jag då 1/6/1/2?
Ehm ska jag då 1/6/1/2?
Ja, om du menar (1/6)/(1/2), dvs så stämmer det.
Yngve skrev:Ehm ska jag då 1/6/1/2?Ja, om du menar (1/6)/(1/2), dvs så stämmer det.
ja det är det jag menar.
OK vet du hur du ska komma vidare?
Tips: Det finns en räkneregel för att dividera två bråktal med varandra.
Yngve skrev:OK vet du hur du ska komma vidare?
Tips: Det finns en räkneregel för att dividera två bråktal med varandra.
Ja jag vet!
(1/6)/(1/2)=(1/6)*(2/1) =1*2/6*1=2/6
2/6=1/3
Bra!
(Men du behöver skräva parenteser runt täljare ich nämnare, så här: (1*2)/(6*1).)
Yngve skrev:Bra!
(Men du behöver skräva parenteser runt täljare ich nämnare, så här: (1*2)/(6*1).)
okej. Men varför gör man det? Ska jag skriva det i min skrivbok så?
ghada.alamer skrev:
okej. Men varför gör man det?
Eftersom det annars betyder
Ska jag skriva det i min skrivbok så?
I skrivboken kan du skriva istället.
Yngve skrev:ghada.alamer skrev:okej. Men varför gör man det? Ska jag skriva det i min skrivbok så?
I skrivborden kan du skriva
Gjorde det. Tack så hemskt mycket för hjälpen! :)
ghada.alamer skrev:
Gjorde det. Tack så hemskt mycket för hjälpen! :)
Vsg.
Jag skrev även till ett svar på din andra fråga.
Yngve skrev:ghada.alamer skrev:Gjorde det. Tack så hemskt mycket för hjälpen! :)
Vsg.
Jag skrev även till ett svar på din andra fråga.
jaha, förlåt såg inte den först.
Inget problem, jag skrev till det i efterskott.