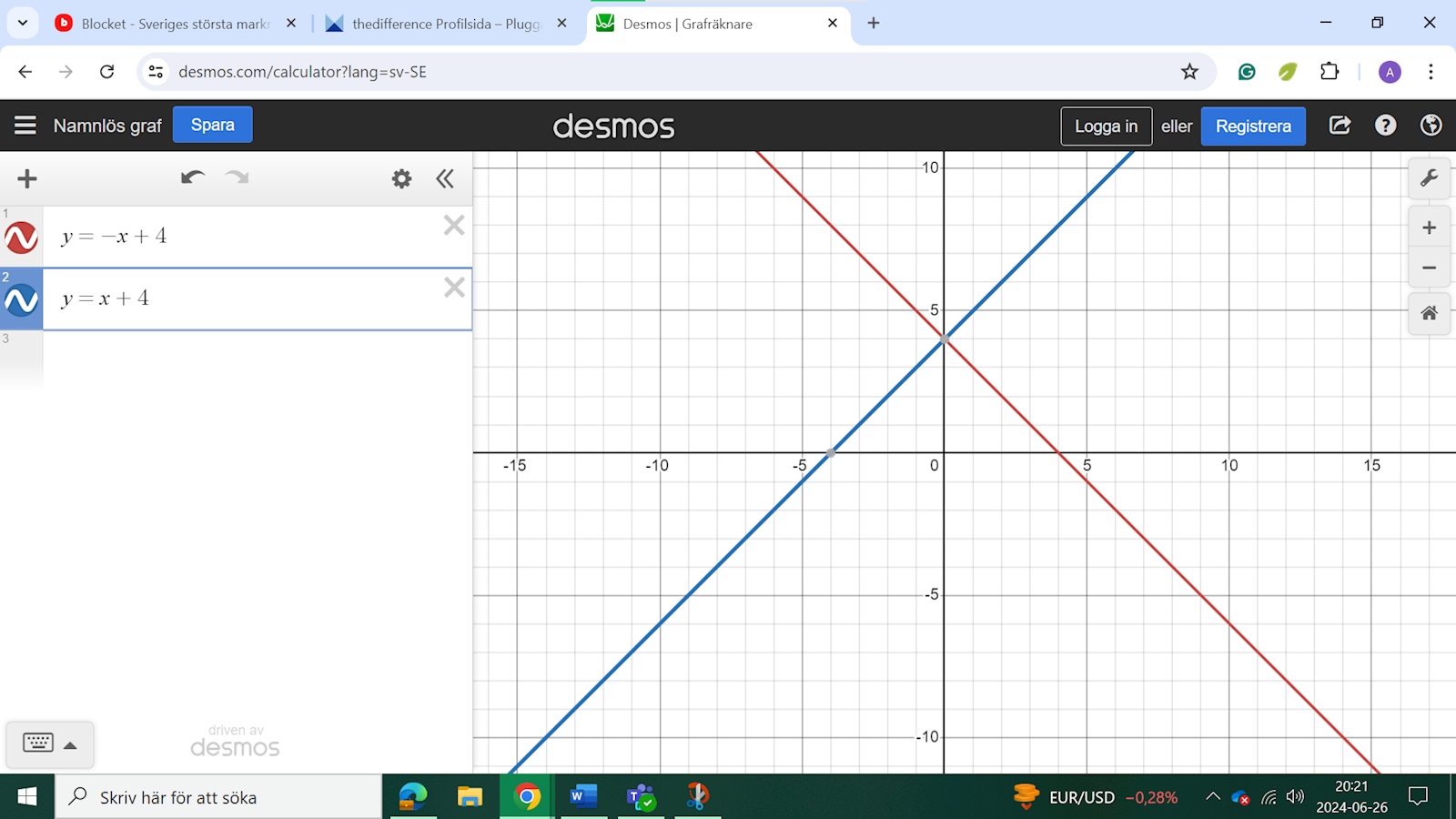
Hur stor area utgörs av linjerna ?

Tänkte så här :

y1-linjen stämmer inte. Båda linjerna skär y-axeln vid y=4.

Tänk även på att ett avstånd aldrig är negativt. Från -4 till 0 är avståndet 4.

Finns en del knep att ta till här vill jag lova, men börja med att få till figuren.

Frågan är hur stor area som linjerna och axlarna begränsar. Du får två trianglar. Det är deras sammanlagda yta som efterfrågas. Eller kan du tänka bort y-axeln och bara köra på en stor triangel.

thedifference skrev:

y1-linjen stämmer inte. Båda linjerna skär y-axeln vid y=4.

Tänk även på att ett avstånd aldrig är negativt. Från -4 till 0 är avståndet 4.

Finns en del knep att ta till här vill jag lova, men börja med att få till figuren.

Figuren var bara en sketch för mig

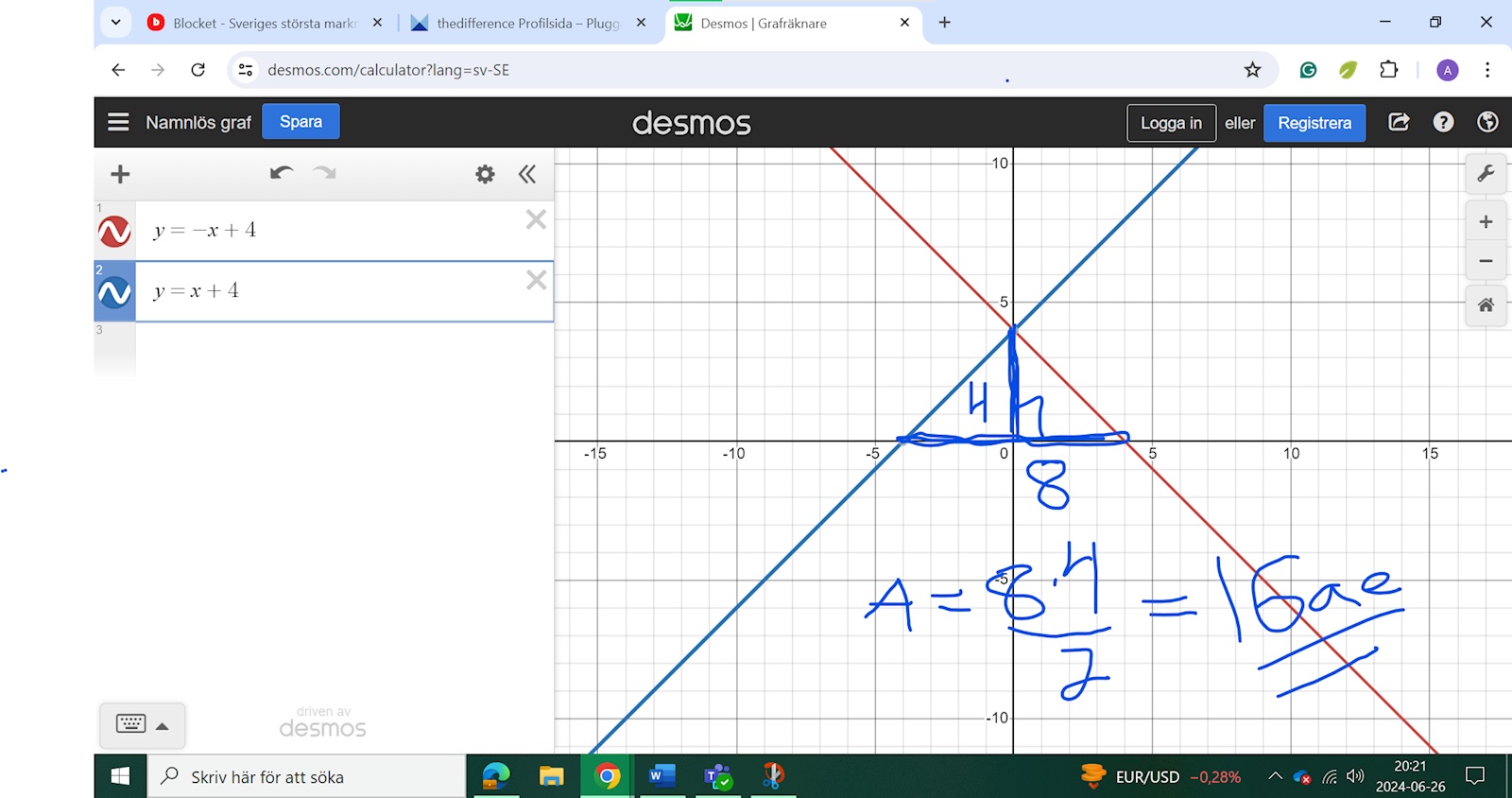
Är det här en snabb och smidig lösning ?

så korrekt svar är Alt.B

Du kommer fram till åttan på lite konstigt sätt (och varför y?), men ja, basen är 8 och svaret är B.

Som alternativ, om du ritar upp det, kan du se att du faktiskt har två trianglar som speglar varandra? Då kan du bara tänka arean för den första, gånger två. Och eftersom arean är b*h/2 kan du istället för att köra 2(b*h/2) bara köra b*h.

thedifference skrev:

Du kommer fram till åttan på lite konstigt sätt (och varför y?), men ja, basen är 8 och svaret är B.

Som alternativ, om du ritar upp det, kan du se att du faktiskt har två trianglar som speglar varandra? Då kan du bara tänka arean för den första, gånger två. Och eftersom arean är b*h/2 kan du istället för att köra 2(b*h/2) bara köra b*h.

Jag förstår inte hur du menar riktigt. 

Jag matade in funktionerna i Desmos

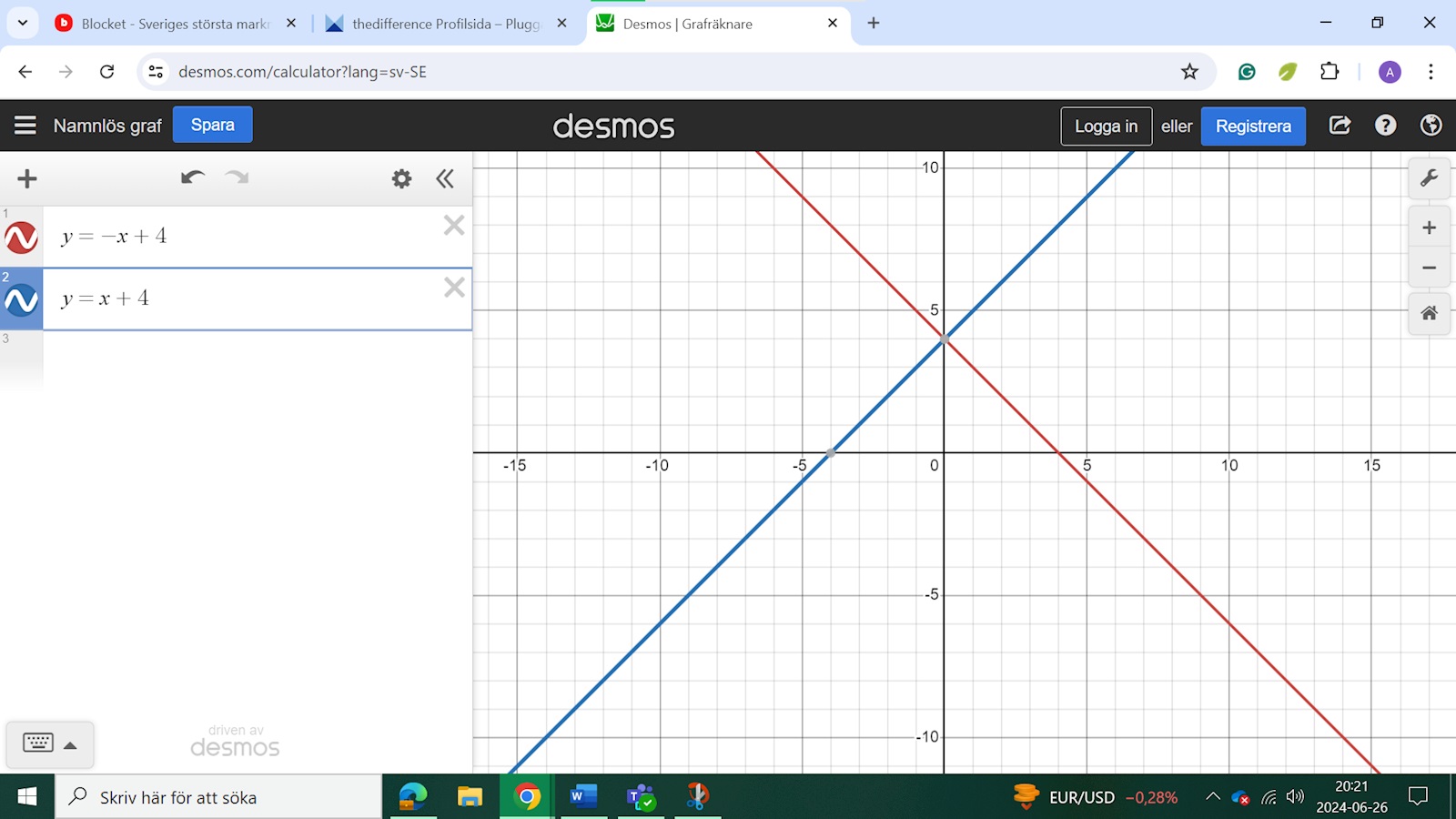
Du har en triangel med hörn i (0,0), (0,4) och (4,0), med y-axeln som höjd och x-axeln som bas, där den röda linjen är hypotenusan. Sen har du en likadan på andra sidan y-axeln, med den blå linjen som hypotenusa.

Arup skrev:

Jag matade in funktionerna i Desmos

Snygg bild, då har du i princip löst den:

$A=\frac{b\cdot h}{2}$

Arup skrev:

Är det här en snabb och smidig lösning ?

Nej, den är inte tydlig.

Se det gulmarkerade, vilket y är det som är -(-4)+4?

Förslag på tydlig lösning (uUtgå från den utmärkta bilden i svar #9):

Vi har en triangel med bas längs med x-axeln och hörjd längd med y-axeln.

Triangelns höjd h ges av avståndet från x-axeln till linjernas skärningspunkt vid (0,4). Höjden är alltså h = 4.

Triangelns bas ges av avståndet mellan linjernas skärningspunkter med x-axeln:

• Linjen y = x+4 skär x-axeln då 0 = x+4, dvs då x = -4
• Linjen y = -x+4 skär x-axeln då 0 = -x+4, dvs då x = 4

Avståndet mellan dessa är b = 4-(-4) = 8.

Triangelns area ges nu av A = b*h/2 = 8*4/2 = 16.

Tillägg: 27 jun 2024 10:20

Ursäkta stavfelen, borde ha kollat dem.