Hur ska man lösa ekvationen och tänka?

Känner du till hur enhetscirkeln fungerar? 

Om ja, rita upp den. 

Notera nu följande:

mellan $0 \leq \theta \leq \pi$ så är y-värdet speglat. Du ser detta enklast om du drar en linje parallell med x-axeln. Med samma logik så kan du snabbt fundera ut hur det borde se ut för cosinus. Cosinus speglas inte i y-led utan i ....

Cosinus speglas såklart i x-led. Så att cos(x)=cos(-x).

Men det jag inte förstår är varför man är tvungen att skriva om sin ursprungsekvation för att få med alla lösningar. Här har jag ritat upp enhetscirkeln:

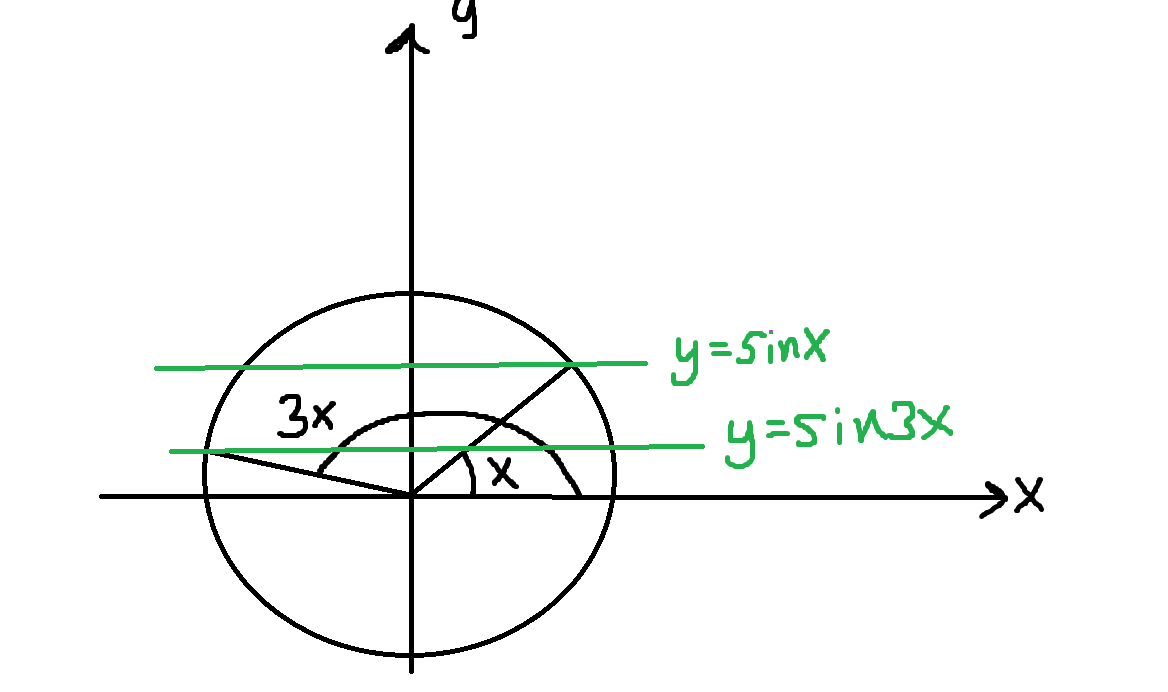
Därför att det finns två fall. De är lika vid $\theta$, och vid $\pi - \theta$. Notera att detta inte måste vara samma vinkeln. 

Om x = 30 grader, så är sin(150)=sin(30), notera att detta är grader, även om jag inte skrivit ut det (skriv aldrig så!!).

Jag vet inte hur familjär du är med att lösa trigonometriska ekvationer, men notera att det finns oändligt med lösningar. Men vi tar en sak i taget. Är du med på varför du måste lösa två fall? 

Om du har $x^2=9$, så har du ju två fall också. Det är ingen skillnad här. Två vinklar producerar samma resultat, precis som en kvadrat (^2, inte geometriska objektet) alltid har två lösningar (rent matematiskt).

Att alla trigonometriska ekvationer har oändligt många lösningar förstår jag, och det är helt logiskt.

Vad exakt menar du med att de är lika vid $θ$ och $π−θ$? Vad syftar "de" på?

Jag tror att jag har ett sätt att tänka på det nu.

Ursprungsradien för $\sin3x$ kommer ju snurra tre gånger så snabbt som radien för $\sin x$ (alltså snurra ett helt varv mycket snabbare). Om man låter $x$öka lika snabbt för båda funktionerna och betraktar radierna kommer man se att radien för $\sin3x$ kommer komma ikapp efter ett visst antal grader. Vid någon punkt kommer de dessutom ha samma y-värde eftersom att radien för $\sin3x$ ligger speglad i y-axlen. Det uppstår alltså fyra lösningar genom spegling i y-axeln:

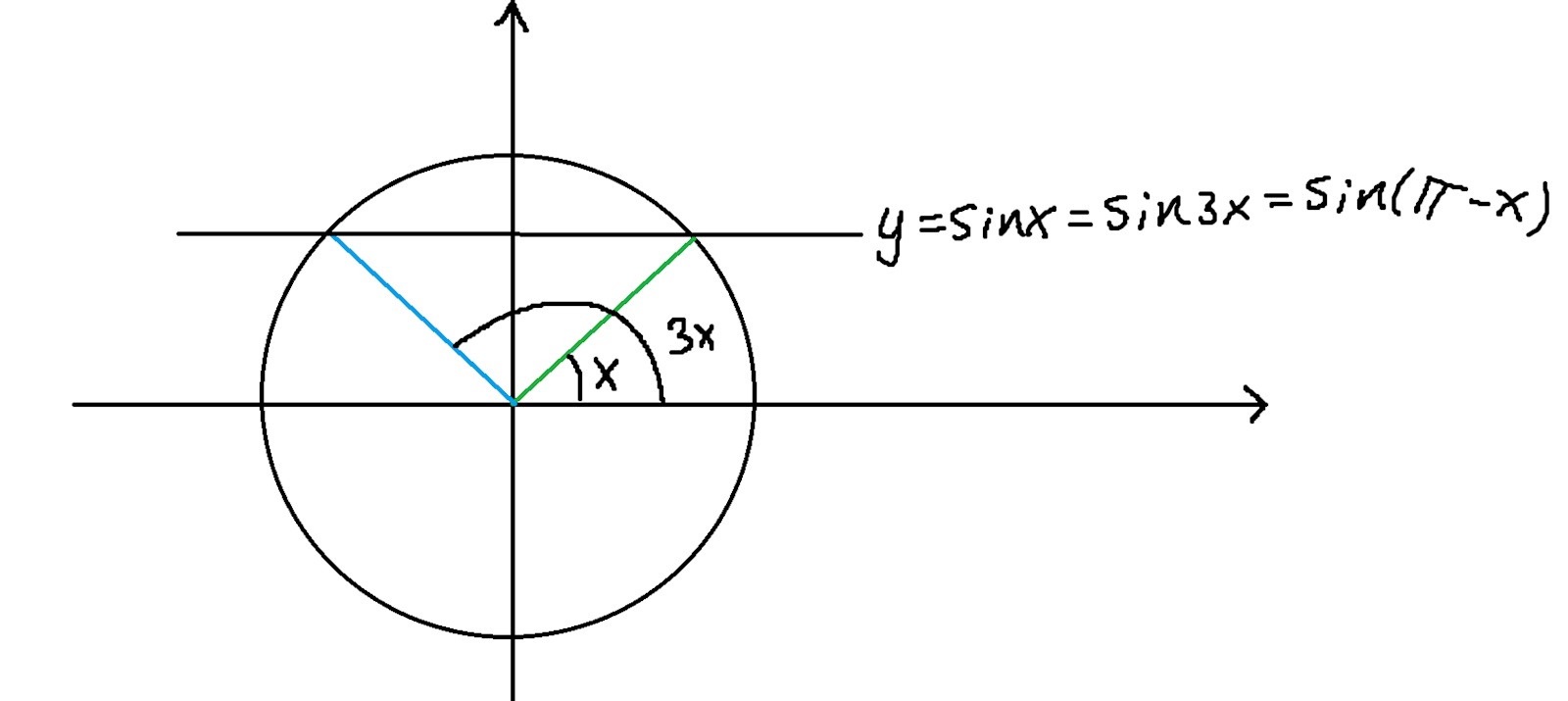
Kan man tänka så?

Så kan du tänka. 

Du kan också tänka att fall två tar hand om fallet när (om möjligt) de är varandras spegelbild.

Jag kom på ett sätt att tänka som (åtminstone för mig) är allra mest logiskt:

$\sin x=\sin (\mathrm{\pi }-\mathrm{x}+2{\mathrm{\pi n}}_1)=\sin (\mathrm{x}+2{\mathrm{\pi n}}_2)$

$\sin 3x=\sin (\mathrm{\pi }-3\mathrm{x}+2{\mathrm{\pi n}}_3)=\sin (3\mathrm{x}+2{\mathrm{\pi n}}_4)$

Sedan löser man alla fyra ekvationer (man kommer få två dubblettlösningar):

$\left\{\begin{array}{l}\mathrm{\pi }-\mathrm{x}+2{\mathrm{\pi n}}_1=\mathrm{\pi }-3\mathrm{x}+2{\mathrm{\pi n}}_3\\ \mathrm{\pi }-\mathrm{x}+2{\mathrm{\pi n}}_1=3x+2{\mathrm{\pi n}}_4\\ \mathrm{x}+2{\mathrm{\pi n}}_2=\mathrm{\pi }-3\mathrm{x}+2{\mathrm{\pi n}}_3\\ \mathrm{x}+2{\mathrm{\pi n}}_2=3\mathrm{x}+2{\mathrm{\pi n}}_4\end{array}\right.$

Detta är visserligen klumpigt, men för mig är det väldigt logiskt och det är ett garanterat sätt att få med alla lösningar.

I varje lösning kommer man få någon term som t.ex. $\mathrm{\pi }({\mathrm{n}}_2-{\mathrm{n}}_4)$ men eftersom $n_2$ och $n_4$ kan anta alla värden på hela $\mathrm{\mathbb{Z}}$ kommer man kunna generalisera dem till ett enda $n\in \mathrm{\mathbb{Z}}$

Jag tror förvirringen kanske kommer från att varför just dra bort pi på VL och inte HL?

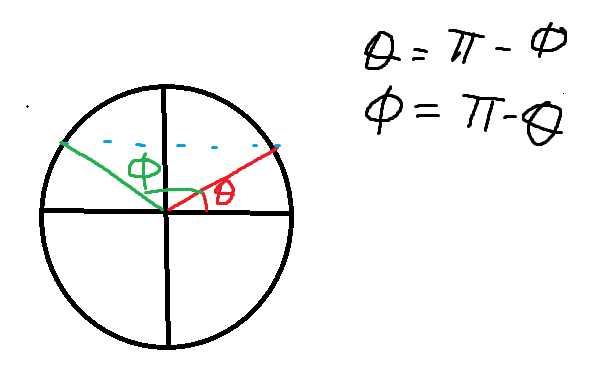
Det spelar ingen roll vilket håll man drar bort pi. Antingen är de varandras spegelbild eller så är det samma värde förskjuten. Det viktiga här är att sin(v) är symmetrisk och periodisk! :)

Jag kommer inte på något super pedagogiskt sätt att förklara varför det blir så. Jag får fundera lite.

Jag förstår. 

Men de fyra ekvationerna jag nämnde ovan kommer väl ge alla lösningar?