Hur ska man kunna veta hur figuren ska se ut i cirkeln? Hur löser man sånt här? Hur tänker man?

Läs det här avsnittet, som går igenom beviset för randvinkelsatsen.

Fråga sedan oss om allt du vill att vi förklarar närmare.

Med hjälp av länken och facit så förstår jag a) uppgiftens svar.
Behöver bara gå igenom uppgiften fler gånger för att liksom få in tänket.

Men b) uppgiften är svårare. 

Så här ser facit bilden ut:
b) medelpunkten ligger utanför randvinkeln
Gällande text uppgiften och förståelse på hur figuren ska se ut, så tänker jag att figuren i cirkeln ska se ut som en "vanlig" randvinkel figur, men flyttar randvinkeln så den ligger utanför medelpunkten men "på samma sida" (enklare för mig att tänka så) och då ser den ut så där. 

men när det kommer till att bevisa randvinkeln här, så tycker jag det är svårt. 

Figuren har en diameter men den delar ju inte vinklarnas vinkelspettsar ? så hur ska man då kunna se liksom att r+r=m  exempelvis? 

För diametern delar ju vinklarna. och bilden har en diameter men den delar ju ingenting?
Och då ser man ju inte yttervinkeln till någon vinkel (tänker på  r+r=m)

...hur ska jag kunna bevisa randvinkelsatsen här på denna figur?

När jag skriver "Fall 1" och "Fall 2" så refererar jag till bevisen på sidan jag länkade till tidigare.

Är du med på följande?

1. Enligt Fall 2 gäller 2*DBA = DOA
2. Enligt Fall 1 gäller 2*CBA = COA
3. Om du nu subtraherar dessa två samband från varandra så får.du
4. 2*DBA-2*CBA = DOA-COA
5. 2*(DBA-CBA) = DOA-COA
6. Efgersom r = DBA-CBA och m = DOA-CIA så får vi att 2*r = m

Tillägg: 28 aug 2024 09:58

Skrivfel på punkt 6. Det ska egentligen stå

"Eftersom r = DBA-CBA och m = DOA-COA så får vi att 2*r = m"

Okej, men jag hänger inte riktigt med. Här är dom figurerna:
fall 1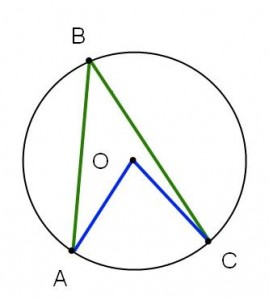                                    
Fall2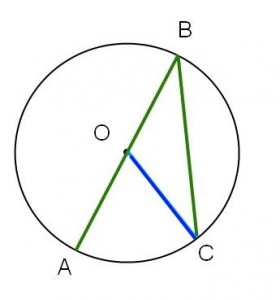
Jag hittar inte D?  liksom vad är "2*DBA = DOA"?

Det är fritt fram att döpa punkter till vad man vill.

Här är det en författare (till facit) som har döpt punkter på en cirkel till A, B, C och D samt medelpunkten.till O.

Sedan är det en annan författare (till sidan jag länkade till) som har döpt punkter på.en cirkel till A, B och C samt medelpunkten till O.

Det är inte samma punkter i dessa fall. Även om de hade varit det så hade de inte behövt heta samma sak.

Som illustration till detta kan jag visa hur kordasatsen ser ut om sträckorna heter något helt annat än a, b, c och d:

Det handlar alltså om att se mönster och likheter och försöka att inte fastna vid vad storheter råkar kallas.

Om du nu tittar på exemplen igen så ser du att Fall 1 beskriver randvinkelsatsen då medelpunkten ligger "inom" vinkeln, och att fall 2 beskriver randvinkelsatsen då medelpunkten ligger på randvinkelns ena vinkelben.

Försök att hitta dessa fall i facits figur, utan att fastna på vad punkterna kallas.

Okej... om jag försöker hitta fall 2 i facit svaret så skulle jag väl säga typ:
Triangeln ABD. En triangel som går igenom medelpunkten men med hjälp av en diameter man ritat. Och då är vinklarna ODB och DBO lika stora om man får använda sig av diametern på det viset? Så som "bevis" skulle väl Triangeln ABD vara en triangel med vinklarna OD och DB som hör ihop vet inte hur jag kan beskriva den "översta" vinkeln i ABD?  Det här känns fel, alltså jag tror jag tänker helt fel...

Om jag ska försöka hitta fall 1 i facit svaret så går de typ inte, men om jag typ försöker se så kanske: CBD?  där typ OCB och BDO tillhör triangeln CBD? 

nej, jag vet inte.. den här är svår!

Vi backar tillbaka lite.

Referenserna "Fall II" och "Fall III" är till sidan jag länkade till I svar #2.

Som jag tolkar din uppgift så gäller a-delen att bevisa randvinkelsatsen i Fall II och b-uppgiften att bevisa randvinkelsatsen i Fall III.

Fråga 1. Är du med på det?

Fråga 2: Förstår du beviset i Fall II?

Fråga 3: Förstår du beviset i Fall III?

Fråga 1: Ja jag är med på det

Fråga 2: ja jag förstår det (förutom det där: 2<OBC, antar att det betyder <OBC 2 gånger, dvs                                                      2*OBC)

Fråga 2: Jag förstår också svaret facit ger mig, med det jag läst från länken du skicka. Det är typ samma.

Fråga 3: Ja jag förstår nästan allt som texten säger och hur dom visar sambandet mellan vinklarna och att det då skulle funka som bevis, (fast även här är jag lite osäker på vad 2<DBA betyder, i 2<DBA=DOC) Jag förstår inte det sista i texten bara, det här "Subtrahera det andra resultatet från det första och vi är klara!"? 

Fråga 3: Jag förstår inte vad facit visar som svar, det förvirrar mig och ser bara super rörigt ut.
Facit svar: 

Med hjälp av den får vi följande samband:∠AOC = 2 ⋅ ABC(enligt randvinkelsatsen)
∠AOD = 2 ⋅ ABD(enligt beviset i 5062a))
Vinklarna r och m kan skrivas som differensen mellan två andra vinklar:r = ∠ABD − ∠ABCm = ∠AOD − ∠AOC == 2 ⋅ ∠ABD − 2 ⋅ ∠ABC == 2(∠ABD − ∠ABC) = 2r.

OK bra.

Jag har nu infört u och v enligt bilden:

Vilket/vilka av följande steg vill du att vi förklarar närnare?

1. u+m = $\angle$ AOD
2. v+r = $\angle$ ABD
3. Enligt a-uppgiften gäller randvinkelsatsen u = 2*v
4. Enligt a-uppgiften gäller randvinkelsatsen u+m = 2*(v+r), dvs u+m = 2*v+2*r
5. Om du subtraherar sambandet i punkt 3 från sambandet i punkt 4 så får du (u+m)-u = (2*v+2*r)-2*v
6. Om du förenklar detta samband får du m = 2*r

==============

Illustration av punkt 3:

Illustration av punkt 4:

Blev det tydligare nu?

Behöver du fortfarande hjälp med denna uppgift?

tack för hjälpen