Hur ska man hantera att z_1 kan väljas godtyckligt?
Halloj!
Jag sitter med uppgiften nedan:

Jag började med att definiera två plan enligt:
Sedan tänkte jag att jag behöver två punkter för att kunna bestämma linjens ekvation, en punkt för att hitta en vektor till linjen från origo och en vektor för att bestämma linjens riktningskoefficient. Vi söker alltså en punkt sådan att vi har:
Vi kan eliminera variabeln och ser då att den kan väljas helt godtyckligt, och kommer fram till ekvationen:
Här tänkte jag att man helt enkelt kan välja två värden på fritt, och då få två motsvarande -värden. Så vi väljer och och får då två punkter:
och
Nu när vi har två punkter som ligger på linjen försöker jag ta fram linjen på vektorform:
Nu är jag dock lite konfunderad på hur man ska fortsätta. Hur ska man bestämma linjen om det finns oändligt många val av ?
Enligt den andra ekvationen i systemet är z1 = 3x1 + 2, så den har ett specifikt värde.
Men jag har ju valt två stycken olika -värden, ett för och ett för . Innebär inte det att jag kommer få olika värden på beroende på vilket jag stoppar in? Men det spelar kanske ingen roll?
Ja, z blir väl olika i Q1 och Q2.
Ah, såklart! Vänta, ska försöka lösa det med detta i åtanke. Förvirrade mig själv genom att använda samma koordinatindexering för båda punkterna.
Alternativ lösningsmetod: När du får normalerna så tydligt kan du fundera på hur dessa normaler förhåller sig till varandra jämfört med planens skärningslinje.
Så, nu kom jag fram till linjen:
När jag grafar i Desmos så verkar det stämma. Men det är inte samma linje som de fick i facit:
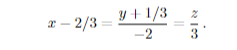
Men de är nog samma, man borde väl bara kunna lägga till 2/3 i alla led och sedan gångra allt med -1?
MrPotatohead skrev:Alternativ lösningsmetod: När du får normalerna så tydligt kan du fundera på hur dessa normaler förhåller sig till varandra jämfört med planens skärningslinje.
Intressant, ska fundera på detta när jag kommer hem sedan!
Visa spoiler
Vi kan låta och lösa ut och .
, . Så linjen blir . Riktningsvektorn kan skrivas för enkelhetens skull. På standardform blir det då .




