Hur ser jag pivåvariablerna?
Hej!
Jag håller på att lösa uppgiften nedan och försöker då gausseliminera och få fram ett trappformatsystem där jag kan se pivåvariablerna. Men, jag har lite svårt att komma på hur jag ska tolka detta "trappformade" system: var blir "hörnen" i trappan (som är väsentligt att ta fram för att kunna avgöra vilka obekanta som är pivåvariabler)? Tack på förhand!

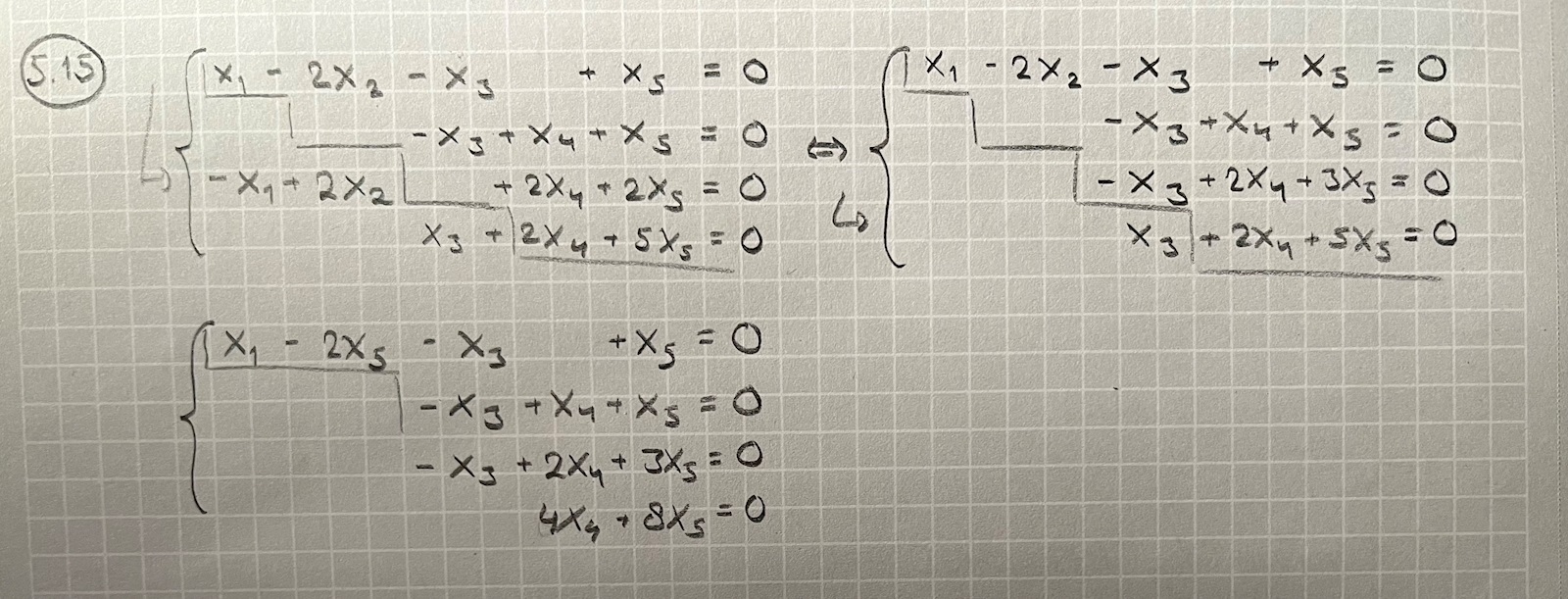
När du gör Gausseliminering radreducerar du först "nedåt". Då får du nollskilda element som följer på enbart nollor i samma rad. Dessa är pivotelementen. Du kan alltid eliminera så att dessa element har enbart nollor under sig.
När du sedan radreducerar "uppåt", ser du till att pivotelementen får nollor även över sig.
Mogens skrev:När du gör Gausseliminering radreducerar du först "nedåt". Då får du nollskilda element som följer på enbart nollor i samma rad. Dessa är pivotelementen. Du kan alltid eliminera så att dessa element har enbart nollor under sig.
När du sedan radreducerar "uppåt", ser du till att pivotelementen får nollor även över sig.
Tack för svaret, men jag lyckas tyvärr inte riktigt förstå vad du menar. Sett till exemplet jag angav i frågan, har jag gjort rätt eller fel då alltså?
Kan du svara på frågorna i uppgiften med hjälp av din gausseliminering? I så fall är den väl bra.
Annars, om man vill ha den typiska formen med ettor i diagonalen och nollor överallt nedanför, så får man ibland byta plats på kolumner när det står en nolla i diagonalen. Man får hålla reda på sådana byten för att det man gör är att byta namn på variablerna.
Om du t.ex. byter plats på kolumn två och tre så står det inte en nolla längre på andra trappsteget (eller hur man ska kalla det).
Vad du menar med "pivåvariabler" vet jag inte riktigt. Du får till slut ett antal variabler som beror av andra variabler samt några variabler (de längst ner) som kan väljas fritt eftersom de har noll som koefficient.
Laguna skrev:Kan du svara på frågorna i uppgiften med hjälp av din gausseliminering? I så fall är den väl bra.
Annars, om man vill ha den typiska formen med ettor i diagonalen och nollor överallt nedanför, så får man ibland byta plats på kolumner när det står en nolla i diagonalen. Man får hålla reda på sådana byten för att det man gör är att byta namn på variablerna.
Om du t.ex. byter plats på kolumn två och tre så står det inte en nolla längre på andra trappsteget (eller hur man ska kalla det).
Vad du menar med "pivåvariabler" vet jag inte riktigt. Du får till slut ett antal variabler som beror av andra variabler samt några variabler (de längst ner) som kan väljas fritt eftersom de har noll som koefficient.
Tack, jag förstår ungefär tror jag. Pivåvariabler är ett begrepp som används frekvent i min lärobok skriven av Jonas Månsson, men ser när jag googlar runt lite att det begreppet inte tycks användas av så många andra. Pivåvariabel är motsatsen till en fri variabel och finnes i "hörnen" när man målat ut sin trappform (det som jag tycker är svårt att lista ut när trappan inte blir, som du säger, med nollor överallt nedanför diagonalen).
Ett pivotelement är det första nollskilda element som inleder en rad.
Det är ett väldigt viktigt koncept och används flitigt i litteraturen.
Några förslag när du Gausseliminerar:
Använd matrisnotation och skriv inte ut i din matris. Men skriv ut nollor där det ska vara nollor i matrisen!
Var tydlig med vilken elementär radoperation du genomför.
Arbeta systematiskt med att eliminera en kolonn i taget.
I ditt första steg adderade du den första raden till den tredje raden och fick
Vi ser att kolonn 1 och 2 bara innehåller nollor under första raden, bra! Vårt mål är nu att bara få nollor i kolonn 3 under andra raden. Vi lägger till -1 av den andra raden till den tredje raden, samt +1 av den andra raden till den fjärde raden. Vi får då
Nu har vi bara nollor under andra radens pivotelement, bra! Slutligen lägger vi till -3 av den tredje raden till den fjärde raden:
Pivotelementet på rad ett är
Pivotelementet på rad två är
Pivotelementet på rad tre är
Pivotelement på rad fyra saknas (det finns inget inledande nollskilt element)
Nu kan vi också utläsa att samt är bundna variabler.
och är fria variabler.
D4NIEL skrev:Ett pivotelement är det första nollskilda element som inleder en rad.
Det är ett väldigt viktigt koncept och används flitigt i litteraturen.
Några förslag när du Gausseliminerar:
Använd matrisnotation och skriv inte ut i din matris. Men skriv ut nollor där det ska vara nollor i matrisen!
Var tydlig med vilken elementär radoperation du genomför.
Arbeta systematiskt med att eliminera en kolonn i taget.
I ditt första steg adderade du den första raden till den tredje raden och fick
Vi ser att kolonn 1 och 2 bara innehåller nollor under första raden, bra! Vårt mål är nu att bara få nollor i kolonn 3 under andra raden. Vi lägger till -1 av den andra raden till den tredje raden, samt +1 av den andra raden till den fjärde raden. Vi får då
Nu har vi bara nollor under andra radens pivotelement, bra! Slutligen lägger vi till -3 av den tredje raden till den fjärde raden:
Pivotelementet på rad ett är
Pivotelementet på rad två är
Pivotelementet på rad tre är
Pivotelement på rad fyra saknas (det finns inget inledande nollskilt element)
Nu kan vi också utläsa att samt är bundna variabler.
och är fria variabler.
Tack för tydlig förklaring! Men, jag förstår inte riktigt hur du ser/vet att "vårt mål nu är att bara få nollor i kolonn 3 under andra raden"? Vad får dig att veta att du vill ha nollor under just andra raden, och inte efter t.ex. första eller tredje raden?
Regeln är ungefär så här:
Det yttersta elementet på varje rad (pivotelementet) ska vara strikt till vänster om pivotelementet på raden under.
I ditt första eliminationssteg fick du fram nollor i kolonn 1 under första raden.
I nästa steg vill du ha nollor under andra raden i kolonn 2. Men det har du redan!
I nästa steg vill du därför ha nollor andra raden i kolonn 3.
Osv.
Du vill ju få till ett tripp-trapp-trull system (trappstegsform). Notera att om man hoppar ned en rad i den slutliga matrisen står nästa pivotelement alltid till höger. Alltså inte direkt under- eller till vänster om.


