Hur ser jag att detta är en linje? (LinAlg)

Den övre ekvationen står för ett plan med normalvektor (2, –2, 1), den undre för ett plan med normalv (2, 0, –1). (Bägge planen går genom origo.)

Två plan som inte är parallella skär varandra längs en rät linje, öppna en bok så får du en illustration till fenomenet.

Om du bildar kryssprodukten mellan de två normalvektorerna får du en riktningsvektor för linjen. Eftersom båda planen går genom origo, går även skärningslinjen genom origo.

Avståndet från punkten till linjen kan bestämmas på flera sätt, det intuitivt naturligaste kanske är att bilda en vektor från den givna punkten till en godtycklig punkt på linjen. Den vektorn bestäms av en parameter, anpassa parametern så att vektorn blir vinkelrät mot linjens riktningsvektor, och bestäm längden. 

Mogens skrev:

Den övre ekvationen står för ett plan med normalvektor (2, –2, 1), den undre för ett plan med normalv (2, 0, –1). (Bägge planen går genom origo.)

Två plan som inte är parallella skär varandra längs en rät linje, öppna en bok så får du en illustration till fenomenet.

Om du bildar kryssprodukten mellan de två normalvektorerna får du en riktningsvektor för linjen. Eftersom båda planen går genom origo, går även skärningslinjen genom origo.

Avståndet från punkten till linjen kan bestämmas på flera sätt, det intuitivt naturligaste kanske är att bilda en vektor från den givna punkten till en godtycklig punkt på linjen. Den vektorn bestäms av en parameter, anpassa parametern så att vektorn blir vinkelrät mot linjens riktningsvektor, och bestäm längden. 

Tack! Jag har påbörjat att lösa uppgiften nu, men lyckas inte komma riktigt i mål. Jag har målat en bild som (om jag förstår uppgiften rätt) illustrerar det uppgiften handlar om. Men, nu när jag har en ekvation för linjen förstår jag inte riktigt delen där jag ska beräkna avståndet. Du nämner att man kan bilda en vektor från den givna punkten till en godtycklig punkt på linjen. Kan denna godtyckliga punkt vara origo? Och en annan fråga: kan man ens skriva en linje på normalform så som jag gjort i slutet av mina beräkningar? Tycker det mer ser ut som ett plan än linje...

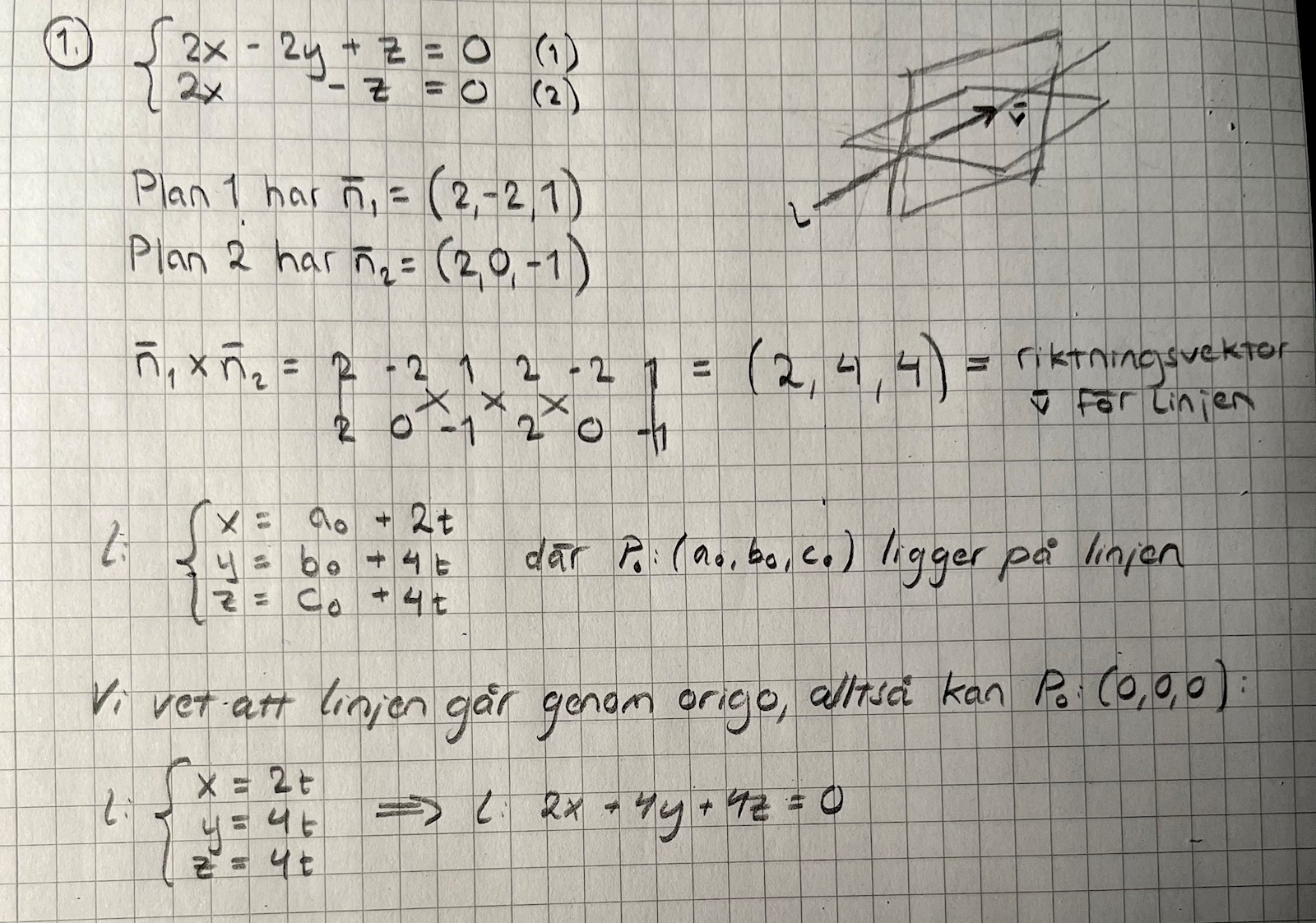
Om jag minns rätt så betyder de båda ekvationerna varsitt plan med olika normaler (2,-2, 1) resp (2,0,-1)  De skär därför varandra i en rät linje.

Du har hittat ett korrekt uttryck för linjen $\mathbf{X}(t)=(2t,4t,4t)$

Nu kan du t.ex. minimera avståndet $d(t)=\|\mathbf{X}(t)-P\|$ med hjälp av derivata. Det kan vara enklare att minimera avståndet i kvadrat, $d^2_{min}$

Du skulle också kunna ta en genväg med kryssprodukten så här:

starboy: Viktigt! Sista raden i din räkning:

(x,y,z) = (2,4,4)t     (1)

2x+4y+4z = 0.        (2)

(1) är en linje. (2) är ett plan. (1) => (2) är så fel det kan bli.

Tänk så här. Vi börjar i det tredimensionella rummet. Alla punkter är tillåtna innan vi har en ekvation. Så lägger vi på villkoret (2). Där försvinner en dimension, kvar är ett tvådimensionellt plan (eller eventuellt en buktig duk i rummet, ifall det inte är linjärt).

I (1) startar vi åter i tre dimensioner. Nu har vi tre ekvationer, det borde bara bli en punkt kvar. Men då glömmer vi parametern t, som gör att punkten kan röra sig längs en kurva (i detta fall en rät linje).

För att lösa uppgiften; du har linjen som jag för enkelhets skull skriver som (x,y,z) = (1,2,2)2t eller

(x,y,z) = (1,2,2)s efter byte av parameter.

Godtycklig punkt på linjen är (s,2s,2s). Vektorn från (1,0,1) till denna punkt är v = (s–1, 2s, 2s–1).

När v vinkelrät mot linjens riktningsvektor (1,2,2) är v som kortast. Då är skalärprodukten noll, dvs

1(s–1)+2(2s)+2(2s–1) = 0

Felräknat nedan, se rättelse efter nästa post.

5s = 3;    s = 3/5 ger v = (2/5, 6/5, 1/5)

Längden av v är [roten ur (4+36+1)] /5 = [sqr 41]/5.

Kan vara felräknat, du får kolla. Men tankegången bör hålla. 

Mogens skrev:

Godtycklig punkt på linjen är (s,2s,2s). Vektorn från (1,0,1) till denna punkt är v = (s–1, 2s, 2s–1).

När v vinkelrät mot linjens riktningsvektor (1,2,2) är v som kortast. Då är skalärprodukten noll, dvs

1(s–1)+2(2s)+2(2s–1) = 0

5s = 3;    s = 3/5 ger v = (2/5, 6/5, 1/5)

Längden av v är [roten ur (4+36+1)] /5 = [sqr 41]/5.

Kan vara felräknat, du får kolla. Men tankegången bör hålla. 

Din uppställning är korrekt, men vad blir egentligen $s$?

Tack D4NIEL, det blev minst ett fel:

1(s–1)+2(2s)+2(2s–1) = 0

9s = 3;    s = 1/3 ger v = (–2/3, 2/3, –1/3)

Längden av v är [roten ur (4+4+1)] /3 = 1

Mogens skrev:

starboy: Viktigt! Sista raden i din räkning:

 

(x,y,z) = (2,4,4)t     (1)

2x+4y+4z = 0.        (2)

 

(1) är en linje. (2) är ett plan. (1) => (2) är så fel det kan bli.

Tänk så här. Vi börjar i det tredimensionella rummet. Alla punkter är tillåtna innan vi har en ekvation. Så lägger vi på villkoret (2). Där försvinner en dimension, kvar är ett tvådimensionellt plan (eller eventuellt en buktig duk i rummet, ifall det inte är linjärt).

I (1) startar vi åter i tre dimensioner. Nu har vi tre ekvationer, det borde bara bli en punkt kvar. Men då glömmer vi parametern t, som gör att punkten kan röra sig längs en kurva (i detta fall en rät linje).

 

För att lösa uppgiften; du har linjen som jag för enkelhets skull skriver som (x,y,z) = (1,2,2)2t eller

(x,y,z) = (1,2,2)s efter byte av parameter.

Godtycklig punkt på linjen är (s,2s,2s). Vektorn från (1,0,1) till denna punkt är v = (s–1, 2s, 2s–1).

När v vinkelrät mot linjens riktningsvektor (1,2,2) är v som kortast. Då är skalärprodukten noll, dvs

1(s–1)+2(2s)+2(2s–1) = 0

Felräknat nedan, se rättelse efter nästa post.

5s = 3;    s = 3/5 ger v = (2/5, 6/5, 1/5)

Längden av v är [roten ur (4+36+1)] /5 = [sqr 41]/5.

Kan vara felräknat, du får kolla. Men tankegången bör hålla. 

Stort tack för bra förklaring! Jag är med på nästan allt du skriver, men det jag tycker är lite konstigt är hur man med linjen (x, y, z) = (1, 2, 2)s kan ta fram den godtyckliga punkten (s, 2s, s). Alltså, hur kan en linje plötsligt bli en punkt?

Det är som min mormor (född på 1800-talet) sade. ”En geometrisk ort är sammanfattningen av alla de punkter som uppfyller ett givet visst villkor.” 

Här är det linjen som är den geometriska orten, och linjen består av

–alla punkter med både y- och z-koordinat dubbelt så stor som x-koordinaten.

–inga andra punkter.

(1)  För varje s ligger (s, 2s, 2s) på linjen.

(2)  För varje punkt på linjen kan man hitta ett s som innebär att (s, 2s, 2s) är punkten.

Det är det vi menar med en godtycklig punkt på linjen, en punkt vars koordinater, för något s, kan skrivas (s, 2s, 2s).

Mogens skrev:

Det är som min mormor (född på 1800-talet) sade. ”En geometrisk ort är sammanfattningen av alla de punkter som uppfyller ett givet visst villkor.” 

Här är det linjen som är den geometriska orten, och linjen består av

–alla punkter med både y- och z-koordinat dubbelt så stor som x-koordinaten.

–inga andra punkter.

(1)  För varje s ligger (s, 2s, 2s) på linjen.

(2)  För varje punkt på linjen kan man hitta ett s som innebär att (s, 2s, 2s) är punkten.

Det är det vi menar med en godtycklig punkt på linjen, en punkt vars koordinater, för något s, kan skrivas (s, 2s, 2s).

Tack så mycket, nu förstår jag!