Hur räknar man fram ett Y värde där x är ett bråk och ekvationen med

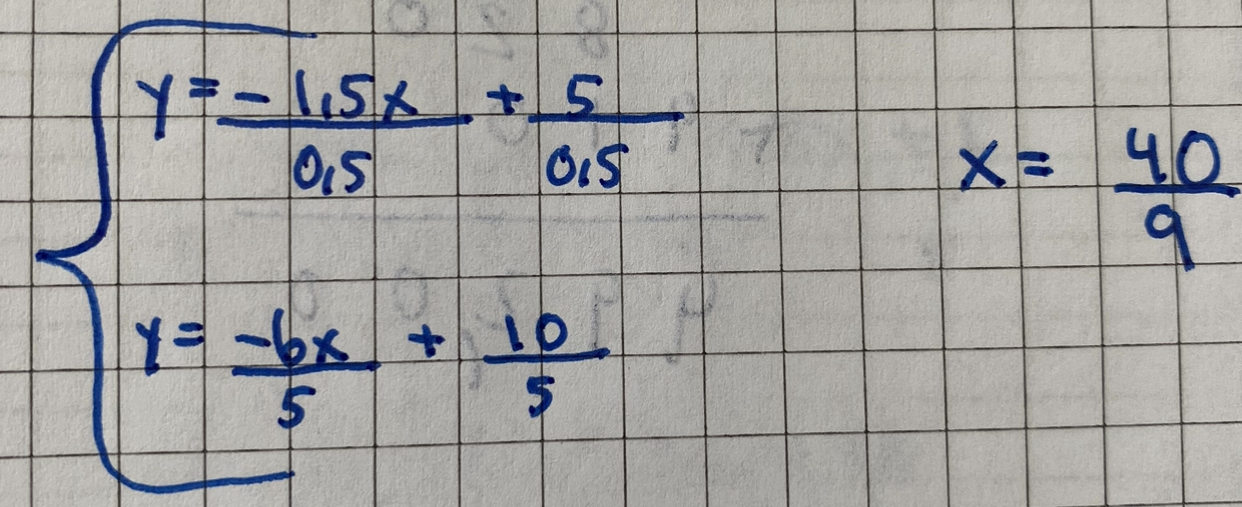
Ta någon av ekvationerna till vänster. Ersätt samtliga x med 40/9. Räkna ut vad y blir; det är vanlig addition, subtraktion, multiplikation och division.

jo, men förstår inte hur det ser ut i en uträkning, för x är ju 40/9?

$$\begin{gathered} y=-\frac{6x}{5}+\frac{10}{5} \\ y=-\frac{6*\left({\displaystyle \frac{40}{9}}\right)}{5}+\frac{10}{5} \end{gathered}$$

https://www.matteboken.se/lektioner/skolar-8/brak/multiplikation-och-division-av-brak

Har prövat att räkna fram svaret på olika vis, (svaret ska bli -10/3), men får inte alls till rätt svar = / 

Du kan börja med att förenkla ekvationerna.

Den första blir då    y = –3x +10

och den andra   y = –1,2x + 2

Blir det lättare då?

Tack för svaret, jag testa med att räkna fram det med hjälp av dina ekvationer men de blir inte rätt ändå. För det ”går runt” bara. Kan visa hur jag tänker när jag räknar med den vanliga ekvationen. 

Här är felet. Du multiplicerar ihop täljarna men inte nämnarna, se bild.

Men eftersom det tidigare står $-\frac{6}{5}\cdot\frac{40}{9}$, dvs en multiplikation av två bråktal, så behöver du inte glra liknämnigt. Istället gäller att $-\frac{6}{5}\cdot\frac{40}{9}=-\frac{6\cdot40}{5\cdot9}$

Att även nämnarna multipliceras samman kan motiveras om man tänker sig att man vill multiplicera 1 med 1. Detta blir 1, men om man uttrycker det som ett bråk:

$$\begin{gathered} 1*1=\frac{2}{2}*\frac{2}{2}=\frac{2*2}{2*2}=\frac{\cancel{2}*2}{\cancel{2}*2}=\frac{\bcancel{2}}{\bcancel{2}}=1 \\ 1*1=\frac{2}{2}*\frac{2}{2}\ne \frac{2*2}{2}=\frac{\cancel{2}*2}{\cancel{2}}=2 \end{gathered}$$

I ditt fall behöver du inte förlänga så du får gemensam nämnare; det är bara att multiplicera direkt:

$\frac{-6}{5}*\frac{40}{9}=\frac{\left(-6\right)*40}{5*9}$

och sedan se vilka förenklingar man kan göra, som Yngve säger.

Tack för svaren. 

ja alltså jag fastnar väl på de sista steget. Men så här räkna jag tillslut fram dit:

En vacker bild med många färger, men inga siffror eller ekvationer.
Vad är det du har kommit fram till?

Naturens skrev:

ja alltså jag fastnar väl på de sista steget. Men så här räkna jag tillslut fram dit:

Din uträkning kan förenklas.

Exempelvis genom att använda additionsmetoden.

Multiplicera då första ekvationen med 10. Den blir då 15x+5y = 50.

Multiplicera andra ekvationen med -1. Den blir då -6x-5y = -10

Addera de två ekvationerna ledvis (dvs lägg ihop vänsterleden för sig och högerleden för sig. Summan blir då 

(15x+5y)+(-6x-5y) = 50+(-10)

Förenkla:

9x = 40, vilket ger x = 40/9.

======

Om du istället vill använda substitutionsmetoden:

1,5x+0,5y = 5

Subtrahera 1,5x från båda sidor och förenkla:

0,5y = 5-1,5x

Multiplicera båda sidor med 2 och förenkla:

y = 10-3x

Sätt nu in (substituera) 10-3x istället för y I andra ekvationen. Du får då

6x+5(10-3x) = 10

Multiplicera i konstanten 5 i parentesen:

6x+50-15x = 10

Förenkla:

50-9x = 10

Addera 9x till båda sidor och förenkla:

50 = 10+9x

Subtrahera 10 från båda sidor och förenkla:

40 = 9x

Dividera båda sidor med 9 och förenkla:

40/9 = x

==========

För att bestämma y-värdet är det enklast att sätta in 40/9 istället för x i den första ekvationen. Du får då

1,5•40/9+0,5y =:5

Förenkla:

60/9+0,5y = 5

Förkorta första termen med 3:

20/3+0,5y = 5

Subtrahera 20/3 från båda sidor och förenkla:

0,5y = 5-20/3

Förläng första termen I högerledet med 3:

0,5y = 15/3-20/3

Förenkla:

0,5y = -5/3

Multiplicera bägge sidor med 2 och förenkla:

y = -10/3

========

Sist men inte minst: Kontrollera att lösningen  x = 40/9 och y = -10/3 stämmer genom att se om den uppfyller båda ekvationerna.

Detta lämnar jag till dig.

Visa gärna hur du gör det så kan vi hjälpa dig med metoden. Detta är ett viktigt steg som inte bör hoppas över.

Tack så mycket för förklaringen. Tror jag måste försöka komma ihåg att sätta in x värdet i ”original ekvationen” (någon av dom) när jag fastnar med att sätta in x i den ekvationen jag gjort om.  Här kommer min kontroll av x & y. 

Naturens skrev:

Tack så mycket för förklaringen. Tror jag måste försöka komma ihåg att sätta in x värdet i ”original ekvationen” (någon av dom) när jag fastnar med att sätta in x i den ekvationen jag gjort om.  

Nej, det måste du inte göra. Du kan använda vilken av ekvationerna som helst (även de omskrivna) för att bestämma y när du väl har bestämt x.

Här kommer min kontroll av x & y. 

Men du måste kontrollera ditt x och y med båda ursprungsekvationerna,inte bara den ena som du har gjort här.