Hur räkna volt och ampere i kopplingsschema?
Hej,
Frågan jag försöker besvara är enligt nedanstående kopplingsschema:
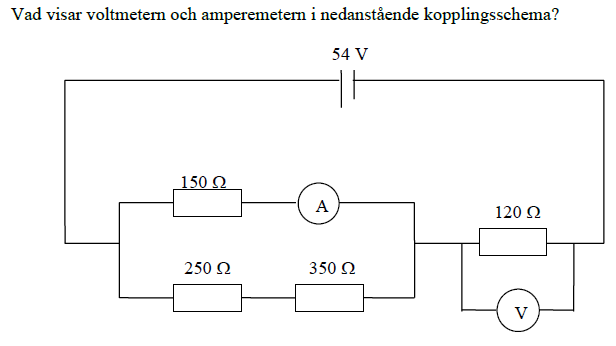
Jag har läst mig till nedanstående:
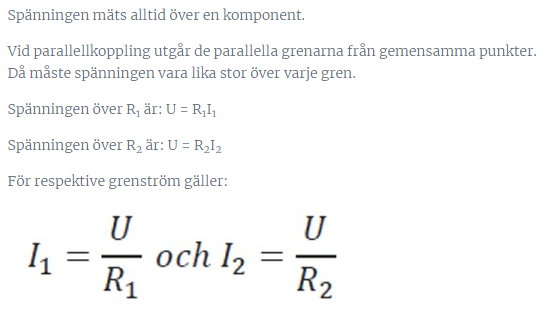
Jag hittade en tråd med liknande frågeställning på forumet och jag förstår uträkningarna. Men jag förstår inte hur man definierar en komponent i kopplingsschemat? Intuitivt vill jag att det ska vara 27V över respektive gren och sen 54V över R4 men jag förstår att det inte är så. Tacksam för hjälp!
Välkommen till Pluggakuten!
Din intuitiva känsla är helt korrekt om du med gren menar parallellkopplingen av 150 Ω med summan av 250 Ω och 350 Ω. Den parallella ersättningsresistansen blir då
Rp = 150•600/(150+600) = 600/(1+4) = 120 Ω
och spänningen på voltmetern visar alltså 27 V.
Fortsätt sedan att beräkna strömmen genom amperemetern.
Ohms lag ger:
ström = spänning * resistans
I = U * R
27 = U * 150
27/150 = 0.18 A
Men jag tror inte att jag var tillräckligt tydlig i min frågeställning.
I kopplingsschemat anges spänningen 54V.
Jag förstår att spänningen i hela systemet anges av U = U1 + U2 i detta fall men jag förstår inte varför man definierar parallellkopplingen som U1 & resistorn vid R4 som U2.
Tacksam för svar!
ellep200 skrev:
Men jag förstår inte hur man definierar en komponent i kopplingsschemat? Intuitivt vill jag att det ska vara 27V över respektive gren och sen 54V över R4 men jag förstår att det inte är så.
Jag förstår inte frågan.
Ersättningsmotståndet beräknades alltså så här:
De är lika stora, så det blir samma spänningsfall över båda. Spänningen som voltmetern över 120 Ω visar är alltså hälften av 54 volt.
Pieter Kuiper skrev:ellep200 skrev:
Men jag förstår inte hur man definierar en komponent i kopplingsschemat? Intuitivt vill jag att det ska vara 27V över respektive gren och sen 54V över R4 men jag förstår att det inte är så.
Jag förstår inte frågan.
Ersättningsmotståndet beräknades alltså så här:
De är lika stora, så det blir samma spänningsfall över båda. Spänningen som voltmetern över 120 Ω visar är alltså hälften av 54 volt.
Tack för svar!
Jag förstår att de är lika stora men det jag har lite svårt att förstå är varför det du har ringat in blir U1. U2 är för mig lättare att förstå.
Men när jag tittar på din cirkel där så tänker jag att:
Huvudströmmen = U = 54
Delström 1 = U 1 = Parallellkopplingen = därför att strömmen sen återgår till samma ledning innan den möter R4
Delström 2 = U2 = R4 för att det är nästa resistor i kopplingen
Därigenom får vi en seriekoppling i vilken U = U1 (om man räknar den som ersättningsresistans) + U2 i detta kopplingsschema.
Tänker jag rätt eller går det ens att förstå vad det är jag är ute efter? xD Tack på förhand!
Du verkar tyvärr blanda ihop grundbegreppen en del då du exempelvis kallar delströmmar för U och kastar om ström och spänning i Ohms lag.
Spänningar betecknar vi oftast med U, strömmar med I och resistanser med R.
Ohms lag är U = R•I


Blir det mer begripligt om vi i stället tänker oss att det är vatten som strömmar?
Allt som kommer från 54V-källan rinner mot de tre inringade motstånden. En del tar vägen genom 150ohm, en del genom 600ohm. Det är ekvivalent med att vattnet strömmar genom 120ohm.
Sedan fortsätter det, alltihop, genom ett annat 120ohm-motstånd.
Jan Ragnar skrev:Du verkar tyvärr blanda ihop grundbegreppen en del då du exempelvis kallar delströmmar för U och kastar om ström och spänning i Ohms lag.
Spänningar betecknar vi oftast med U, strömmar med I och resistanser med R.
Ohms lag är U = R•I
Ja det har du såklart rätt i & det var slarvigt av mig. Men jag har ändå misslyckats med att formulera den egentliga frågan.
Bubo skrev:Blir det mer begripligt om vi i stället tänker oss att det är vatten som strömmar?
Allt som kommer från 54V-källan rinner mot de tre inringade motstånden. En del tar vägen genom 150ohm, en del genom 600ohm. Det är ekvivalent med att vattnet strömmar genom 120ohm.
Sedan fortsätter det, alltihop, genom ett annat 120ohm-motstånd.
Ja, tack för analogin. Det var så jag föreställde mig att det fungerade men det har inte beskrivits på ett tillräckligt konkret sätt i boken eller någon annanstans för att jag skulle vara säker på att det var så det funkade. Stort tack för hjälpen!



