hur många svar efter roten ur
Hej jag behöver hjälp att förstå när man i andragradsekvationer bara får 1 svar efter man tagit roten ur, tror det kallas dubbelrot eller något sådant. Behöver också hjälp att förstå när det är man får 2 olika svar efter roten ur och när man inte får några reela svar.
Kan du ge något exempel?
Ekvationen x2-4=0 ger 2 svar x=±2
Men ekvationen x2+6x+9=0. insatt i PQ-formeln ger x=-3±√32-9x=-3±√9-9x=-3±√0
Eftersom att det blir 0 under roten ur tecknet så finns det endast en lösning, som är -3. En s.k dubbelrot.
jag hade uppgiften: bestäm a så att det blir en dubbelrot i: 2x^2-8x+a=0. Jag fick fram att a skulle vara 8 efter att ha använt formeln D=b^2-4ac. Efter jag löst uppgiften undrade jag hur man besämmer a för att få olika svar efter man tagit roten ur och det är det jag vill ha hjälp med
Hej!
Så här brukar jag tänka:
Ta andragradsekvationen och skriv den på pq-formeln.
x2+px+q=0
1. Om det tal som står under rottecknet är positivt kommer vi få två olika svar, två rötter.
2. Om det tal som står under rottecknet är noll kommer vi få ett svar, en dubbelrot.
3. Om det tal som står under rottecknet är negativt kommer vi inte får några reella svar.
Grafiskt:
1. Ritar du upp denna kurva kommer den korsa x-axeln på två ställen, dessa punkter är de två rötterna, exempelvis:
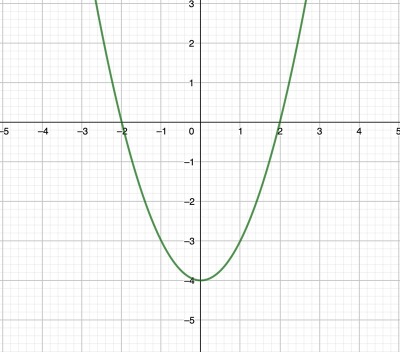 (De två rötterna är x = -2 och x = 2.)
(De två rötterna är x = -2 och x = 2.)
2. Ritar du upp denna kurva kommer den korsa x-axeln på ett ställe, denna punkt är dubbelroten, exempelvis:
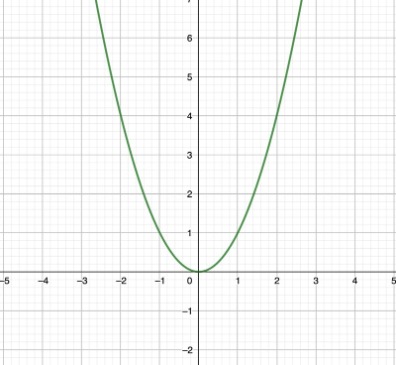
(Roten är x = 0)
3. Ritar du upp denna kurva kommer den inte korsa x-axeln alls, exempelvis:
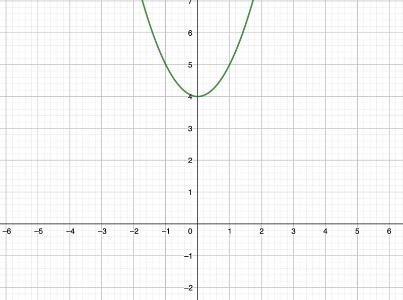

.jpg?width=80&crop=0,0,80,80)
