Hur många rätblock av 60 kuber

Försöker förstå hur jag räknar ut hur många olika typer av rätblock som kan byggas av 60 kuber.

Jag vet hur man använder multiplikationsprincipen för att räkna ut hur många olika flaggor med x antal fält som man kan kan måla av x antal färger, men förstår inte hur jag ska/kan använda samma princip på frågan ovan. Det är inte fler rätblock än att jag kan testa mig fram, men vill förstå multiplikationsprincipen för frågan ovan.

Hej och välkommen till PA!

Volymen av en kub med sidorna a, b och c är: $a \times b \times c$

Du vet också att: $a \times b \times c = 60$

Dessutom måste ju a, b och c vara heltal.

Ett av de möjliga rätblocken är: $2 \times 5 \times 6$

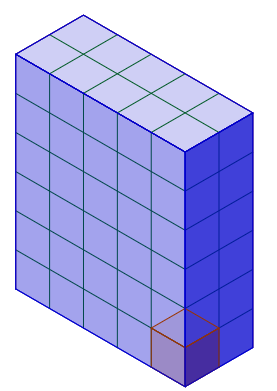
Man kan förstås bygga ett rätblock som är: $2 \times 6 \times 5$

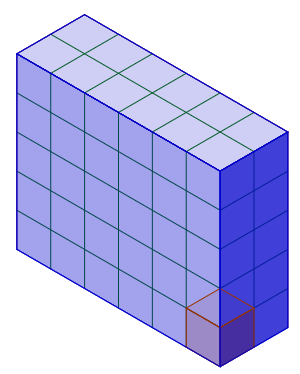
Det är dock samma rätblock, fast tippat över ena kanten, så det räknas inte.

För att se hur många olika rätblock vi kan bygga, så får vi sätta upp en regel: $a \leq b \leq c$

Då kan vi bygga $2 \times 5 \times 6$ men inte $2 \times 6 \times 5$ .

Återstår att finna hur många olika varianter vi kan hitta.

Jag bjuder på en till, som kanske är lätt att missa: $1 \times 1 \times 60$

För att veta vilka möjliga värden du har på a, b och c så får du hitta alla tal som jämnt delar 60. De första är 1 och 2; de sista är 30 och 60: $1, 2, . . ., 30, 60$

Svara