Hur långt har hopparen fallit
Hej,
Behöver råd på fråga 3394 här.
Jag måste hitta antiderivatan till uttrycket och likställa det med 40 och räkna ut. Är vad jag tänker.
Jag kommer då fram till: 80t^2 - e^ln0.88t = 40.
Men jag kan inte utvärdera det.. ja, om det ens är rätt. Det kan eventuellt vara så att tanken är grafiskt verktyg..

Nej, det är hastigheten som är 40. Lös ut tiden och använd den i den primitiva funktionen.
Vet inte hur man löser ut t.
Får svaret till 2351.5 meter. Det känns inte rimligt. Kollar facit. Nej 120 meter..
Det du ska lösa är ekvationen:
Då får du tiden där hastigheten är 40 m/s. Sedan integrerar du helt enkelt.
naytte skrev:Det du ska lösa är ekvationen:
Då får du tiden där hastigheten är 40 m/s. Sedan integrerar du helt enkelt.
Yes.. men jag kan inte lösa den. Eller så beskriver jag antiderivatan fel. Gör såhär;
Eller det är tydligen rätt enligt Trinitys svar där. Då är antiderivatan fel..


Behöver man använda någon regel ifrån Matte 4 för att lösa integralen? Tycker jag gör det på alla sätt som boken har gått igenom hittills men får absolut inte svaret 120.
Antar att jag missar något uppenbart som vanligt men.
Har testat: 80t(t-e^ln0.88t)
80t^2 - 80^t(e^ln0.88t)
80t(1-e^ln0.88t)
Säkert flera, går lite i cirklar bara just nu.
Det är löst med digitalt verktyg i Facit av någon anledning.
Man kan inte integrera produkter så. Lättast är att multiplicera in 80 i parentesen och integrera termerna som uppstår för sig.
Det är ju en matte 4 grej, produktregeln eller någonting?
Okej, jag förstår inte hur du menar exakt, det är just det jag tycker att jag redan gör?
80* 5.422 = 433.776
(80*5.4222)0.88^5.4222 = 216.783
434-217 = 217.
Det är en deriveringsregel!
Försök att integrera 80-80*0,88t.
Jaha..
Ja, det är det jag försöker göra.
80t - (80t*0.88^t)
433.8 - 216.9 = 216.9
Du integrerar potensfunktionen fel.

Använd formeln längst ner.
Okej. Verkar göra något mer fel eller förstår ändå inte hur jag ska ställa upp exponentdelen.
Nu fick jag följande:

Att lägga på ett t gör du på termer, inte på en konstant faktor.

https://mathb.in/80191
MrPotatohead skrev:Att lägga på ett t gör du på termer, inte på en konstant faktor.
Jaha...men om man multiplicerar in 80 först så är det väl en term sen i och med att det står minus mellan 1 och exponentdelen? Och om inte, ska inte 1an bli ett t??
Struntsamma, jag orkar inte mer. Krävs allt av mig för att jag ska förstå varenda minimalt steg av allt.
Tack för hjälpen 👍
Du behöver inte ens multiplicera in faktorn innan du tar fram den primitiva funktionen.
Detta eftersom om F(x) är.en primitiv funktion till f(x) och k är en konstant så gäller det att k*F(x) är en primitiv funktion till k*f(x). Det här följer direkt av deriveringsregeln i ditt formelblad:

========
Vi tar ett enklare exempel för att förtydliga.
Säg att du vill ta fram en primitiv funktion till 3(1+x).
- En metod är att först multiplicera in konstanten 3 i parentesen, vilket ger 3+3x, och sedan ta fram en primitiv funktion, vilket ger 3x+3x2/2. Detta kan skrivas 3(x+x2/2).
- En annan metod är att först ta fram en primitiv funktion till 1+x, vilket ger x+x2/2, och sedan använda regeln om F(x), f(x) och k jag beskrev ovan, vilket ger dig att en primitiv funktion till 3(1+x) är 3(x+x2/2).
De båda metoderna ger alltså samma resultat.
Hängde du med?
Och kan du använda det i denna uppgift?
Dkcre skrev:MrPotatohead skrev:Att lägga på ett t gör du på termer, inte på en konstant faktor.
Jaha...men om man multiplicerar in 80 först så är det väl en term sen i och med att det står minus mellan 1 och exponentdelen? Och om inte, ska inte 1an bli ett t??
Struntsamma, jag orkar inte mer. Krävs allt av mig för att jag ska förstå varenda minimalt steg av allt.
Tack för hjälpen 👍
Ja asså allt du skulle integrera var ju 80-80*0,88t men du fick ju rätt på första delen så visade bara andra.
Yngve skrev:Du behöver inte ens multiplicera in faktorn innan du tar fram den primitiva funktionen.
Detta eftersom om F(x) är.en primitiv funktion till f(x) och k är en konstant så gäller det att k*F(x) är en primitiv funktion till k*f(x). Det här följer direkt av deriveringsregeln i ditt formelblad:
========
Vi tar ett enklare exempel för att förtydliga.
Säg att du vill ta fram en primitiv funktion till 3(1+x).
- En metod är att först multiplicera in konstanten 3 i parentesen, vilket ger 3+3x, och sedan ta fram en primitiv funktion, vilket ger 3x+3x2/2. Detta kan skrivas 3(x+x2/2).
- En annan metod är att först ta fram en primitiv funktion till 1+x, vilket ger x+x2/2, och sedan använda regeln om F(x), f(x) och k jag beskrev ovan, vilket ger dig att en primitiv funktion till 3(1+x) är 3(x+x2/2).
De båda metoderna ger alltså samma resultat.
Hängde du med?
Och kan du använda det i denna uppgift?
Hej Yngve,
Ja, jag förstår dina exempel. Eller jag.. är med på reglerna är mer korrekt?
Lyckas lösa det med ena metoden men inte med andra. Jag förstår inte vad jag ska göra med minustecknet om jag multiplicerar in 80. Jag får 80t-(80e^ln0.88t)/ ln0.88. Utvärderar jag uttrycket i parantesen får jag svaret -312.9, men sedan har jag ju då ett minustecken framför, vilket gör att -312.9 blir ett positivt tal = 312.9 istället. Vilket är fel för då blir svaret 745.9.
Hanterar jag det istället som att minus hamnar innanför parantesen får jag (-80e^ln0.88t)/ln0.88 = 312.9.
I vilket fall fel.. så antingen hanterar jag teckenväxlingen fel eller så har jag inte skrivit uttrycket korrekt.
Jag förstår att det är konstigt, men jag försöker verkligen.

Hjälper detta?
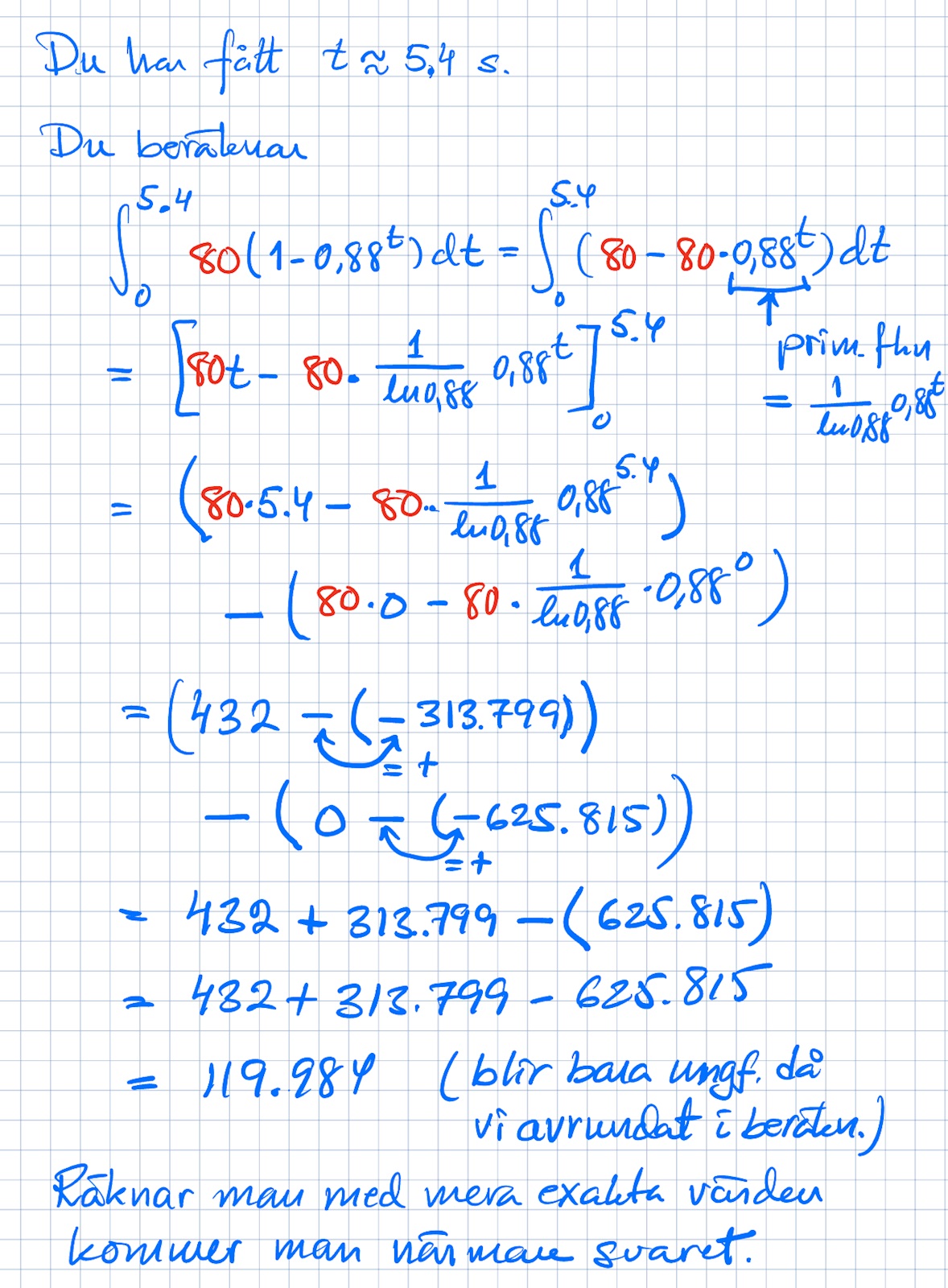
Hej, ja,
Jag fick till det nu..
Tack.
Delar du upp 0.88^t/ln0.88 för att det ska bli tydligare eller varför gör man så? Ser ju bättre ut i varje fall
Dkcre skrev:Hej, ja,
Jag fick till det nu..
Tack.
Delar du upp 0.88^t/ln0.88 för att det ska bli tydligare eller varför gör man så? Ser ju bättre ut i varje fall
Hur menar du med "dela upp"? Jag är inte helt med.
Att skriva 0.88^t/LN0.88 som 1/ln0.88 * 0.88^t.
Det kan vara för tydligheten ja. Det spelar ingen roll.






