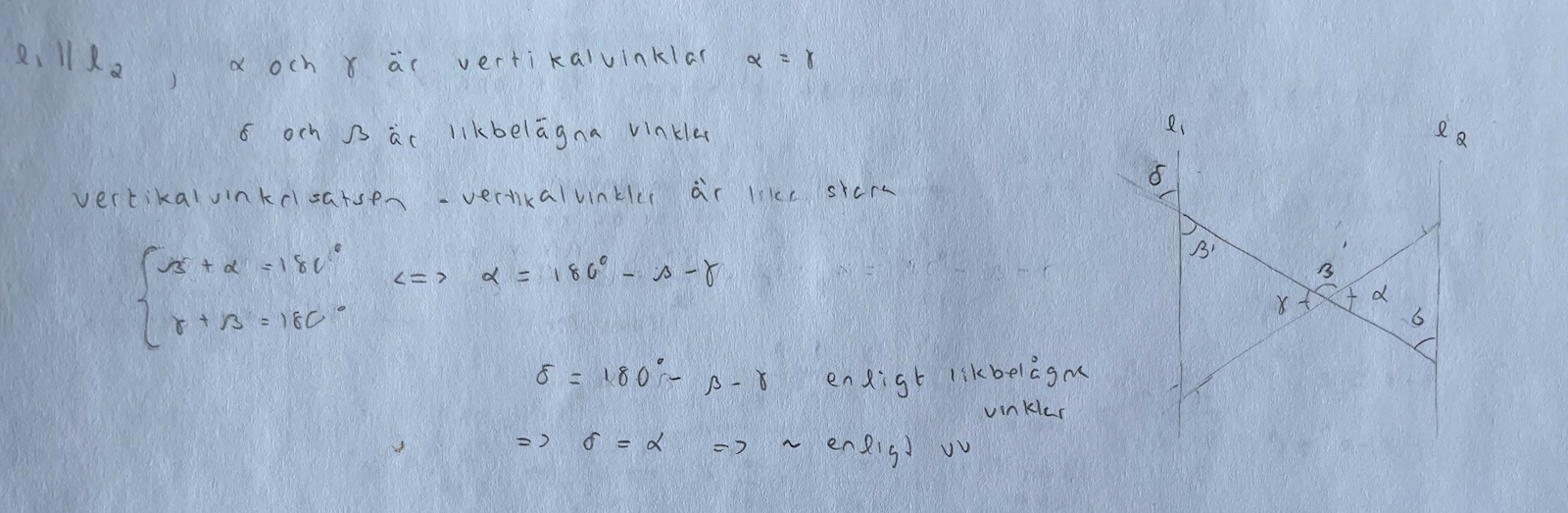Hur lång är det kortaste avståndet från Alfons till Berit?
Alfons bor i hus A och ska besöka sin kompis Berit som bor i AB, se vägkartan. Alla mått på (den dåligt ritade) kartan är i km, alla vägar är raka, och de två vägarna som går i nord-sydlig riktning är parallella. Hur lång är den kortaste vägen från hus A till hus B?
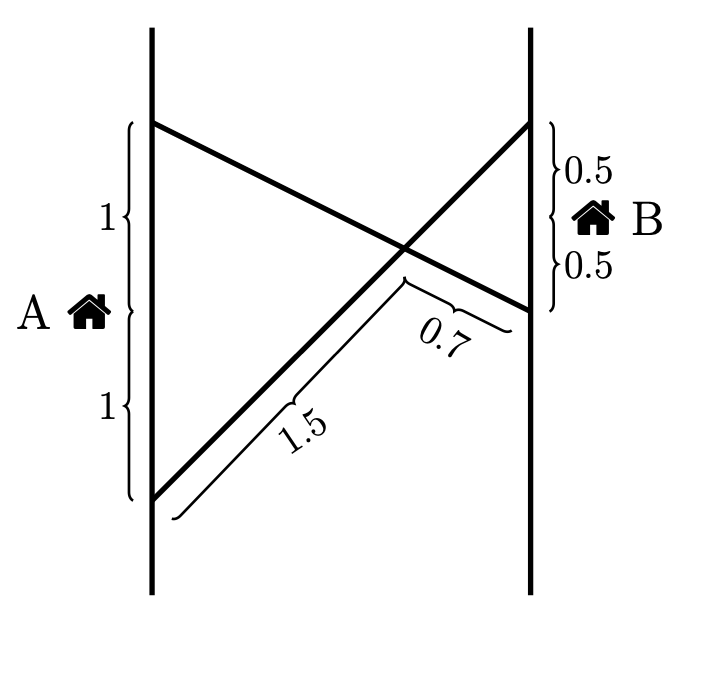
Jag började först att ställa upp vertikalvinkelsatsen med satsen om att vinkelsumman i en triangel är 180. Känner att jag inte kommer någon vart då trianglarna inte är kongruenta eller det finns något likformighetsfall?
De 2 trianglar som bildats i figuren är likformiga.
Säg till om du behöver hjälp med att bevisa det.
joculator skrev:De 2 trianglar som bildats i figuren är likformiga.
Säg till om du behöver hjälp med att bevisa det.
Önskar hjälp att bevisa att de är likformiga. Deras vertikalvinklar är ju samma och basen är ju proportionella men förstår inte hur man motiverar det vidare.
Om man har två parallella linjer så är alternatvinklarna lika. Repetition från Ma2.
Smaragdalena skrev:Om man har två parallella linjer så är alternatvinklarna lika. Repetition från Ma2.
Jag tänkte också på alternatvinklarna men blir förvirrad över vad som är alternatvinklarna. Är det såhär? Då kan man motivera att de är likformiga enligt vv?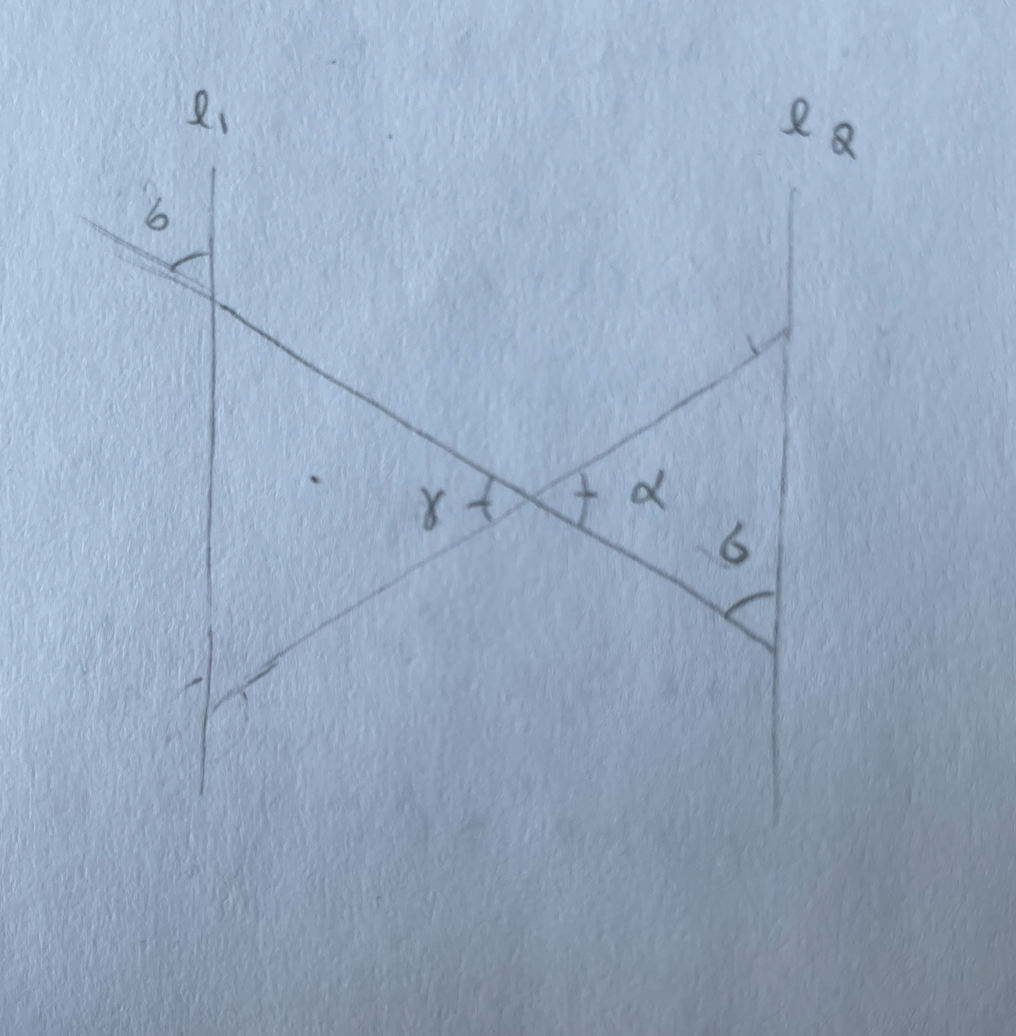
Dina vinklar i mitten är vertikalvinklar så de är lika med varandra. Dina vinklar b är inte alternatvinklar utan likbelägna vinklar,men sådana är också lika med varandra om det handlar om parallella linjer. Kombinera likbelägna vinklar med vertikalvinklar så ser du att vinkeln nedanför det översta b-et är lika med det högra b-et.
Är detta ett korrekt bevis av likformighet VV?