Hur kommer dom fram till svaret
uppgiften är:
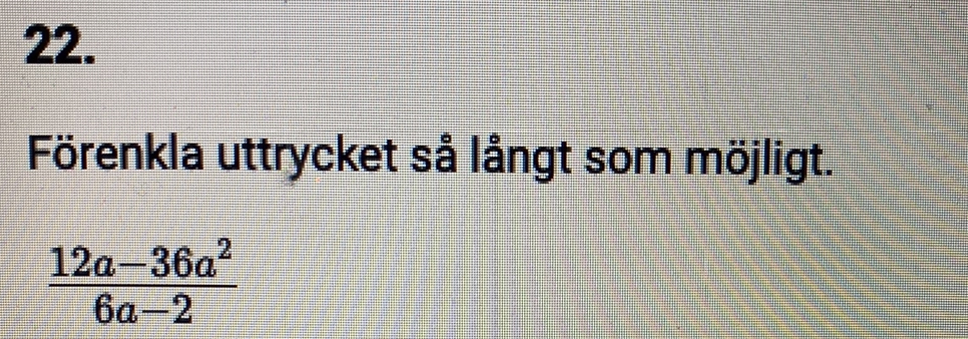
så jag har räknat:
 jag får de till 6a men facit säger -6a
jag får de till 6a men facit säger -6a
Vad händer med faktorn i täljaren när du förenklar?
När du förenklar råkar du förenkla bort ett minustecken. Du behöver börja med att bryta ut i nämnaren, och sedan förenkla:
Det är troligtvis därför du och facit inte får samma svar. :)
Hej, Tack för svaret. 6a i täljaren blir liksom det som är kvar efter att jag förenklat parenteserna först, tänkte att de typ skulle gå att göra så?
Tänkte att -2 i nämnaren tillhörde 2:an & att det var ett -2 & inte bara en 2:a. Men menar du typ så här? 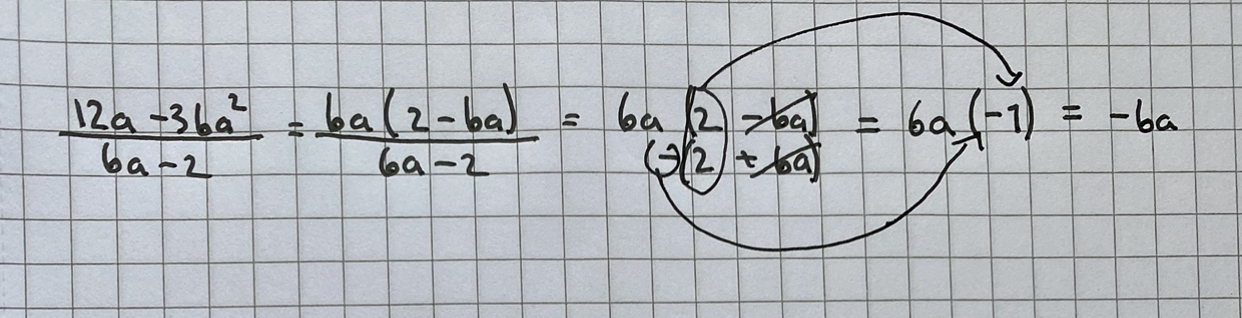 försöker bara se stegen från uppgift till svaret
försöker bara se stegen från uppgift till svaret
Du kan fokusera på delar av ett uttryck, det går bra, men du måste vara tydlig med att det är det du gör. Du kan exempelvis skriva:
Uttrycket kan förenklas till genom att...
Det innebär att kan skrivas som .
Hur menar du när du skriver:
Tänkte att -2 i nämnaren tillhörde 2:an & att det var ett -2 & inte bara en 2:a.
? :)
Minustecknet i täljaren tillhör tvåan, det stämmer. Det vi kan göra är att bryta ut -1 från nämnaren. Då får vi omskrivningen , så att faktorn finns i både täljare och nämnare, och kan förkortas bort.
Tack för förklaringen. Det jag mena med att -2 tillhör 2:an i nämnaren är att jag tänkte att:
2:an i täljaren och -2 i nämnaren tar ut varandra, så som -6a i täljaren och +6a i nämnaren tar ut varandra. Tänkte inte på att ta 2/2 =1 sen lägga till - på 1:an så det blir -1. Men de kanske är så man ska göra med tanke på att jag har 6a som jag ska multiplicera med något, alltså -1 då.
Super tack igen.
Hmmm, okej jag tror att jag förstår vad du menar. Det är viktigt att komma ihåg att endast faktorer (multiplikation och division) kan förenklas bort. Det går inte att förenkla exempelvis som , utan för att förenkla måste du först få ihop faktorer, exempelvis genom att skriva om till multiplikation:
I denna uppgift förenklar vi bort faktorn . Det går bra eftersom det är en faktor, även om den innehåller addition/subtraktion. :)
Varsågod! :)


