hur kom de på lösningen?

Hodlys skrev:

Hej!

Jag fattar inte liksom hur de kom på att lösa uppgift b) på det sättet:

 

Hur fick de just idén att använda sig av u=k*z?

För att de själva hade konstruerat uppgiften och visste om svaret från början, skulle jag tro.

Om vi inte vet det kan vi sätta z = a+bi och u = c+di. Då är z+u = a+c+(b+d)i och

$\left|z\right| = \sqrt{a^2+b^2},\left|u\right| = \sqrt{c^2+d^2}, |z+u| = \sqrt{{(a+c)}^2+{(b+d)}^2}$

Jag satte in alla bokstäver, kvadrerade båda sidor, multiplicerade ihop parenteser, kvadrerade igen och fic bara en föra av bokstavssallad - och sedan råkade jag slarva bort mina fina beräkningar i cyberspace, men de ledde ändå ingenstans, så jag lägger inte in dem en gång till.

Då får vi pröva en annan metod, som vanligt kan man rita!

Nu försöker jag först "rita i huvudet", få se om det funkar... Om summan av argumenten för två komplexa tal skall vara lika med argumentet för summan av de båda talen så krävs det att de båda talen "pekar åt samma håll", d v s att de har samma argument. Om de inte pekar åt samma håll, kommer summan inte "bli rakt ut från origo" utan någonannanstans, som då är närmare. Det betyder att om z = ax+bi = r(cos(v),i sin(v)) så måste u = kr(cos(v),i sin(v) = ka+kbi = k(a+bi) = kz, så då har vi kommit fram till det som facit ville.

Här är en längre beräkning som ger önskat resultat.

Låt $z = 1 + 3i, u = a + bi$, men $z$ borde kunna vara godtyckligt.

$|z + u| = |z| + |u|$

$|(a + 1) + (b + 3)i| = |1 + 3i| + |a + bi|$

$\sqrt{(a + 1)^2 + (b + 3)^2} = \sqrt{1 + 9} + \sqrt{a^2 + b^2}$

$\sqrt{a^2 + 2a + 6b + b^2 + 10} = \sqrt{10} + \sqrt{a^2 + b^2}$

$a^2 + 2a + 6b + b^2 + 10 = {\left(\sqrt{10} + \sqrt{a^2 + b^2}\right)}^2$

$a^2 + 2a + 6b + b^2 + 10 = 10 + 2\sqrt{10}\sqrt{a^2 + b^2} + (a^2 + b^2)$

$2a + 6b = 2\sqrt{10}\sqrt{a^2 + b^2}$

$(a + 3b)^2 = 10(a^2 + b^2)$

$a^2 + 6ab + 9b^2 = 10a^2 + 10b^2$

$9a^2 - 6ab + b^2 = 0$

$(3a - b)^2 = 0$

$3a - b = 0$

$b = 3a$.

Insättning ger nu $u = a + 3ai = a(1 + 3i) = az$, där $a$ är en godtycklig konstant.

Hoppas det hjälper!

Hodlys skrev:

Hej!

Jag fattar inte liksom hur de kom på att lösa uppgift b) på det sättet:

 

Hur fick de just idén att använda sig av u=k*z?

Deras lösningen är inte speciellt bra.

Tänk geometriskt istället

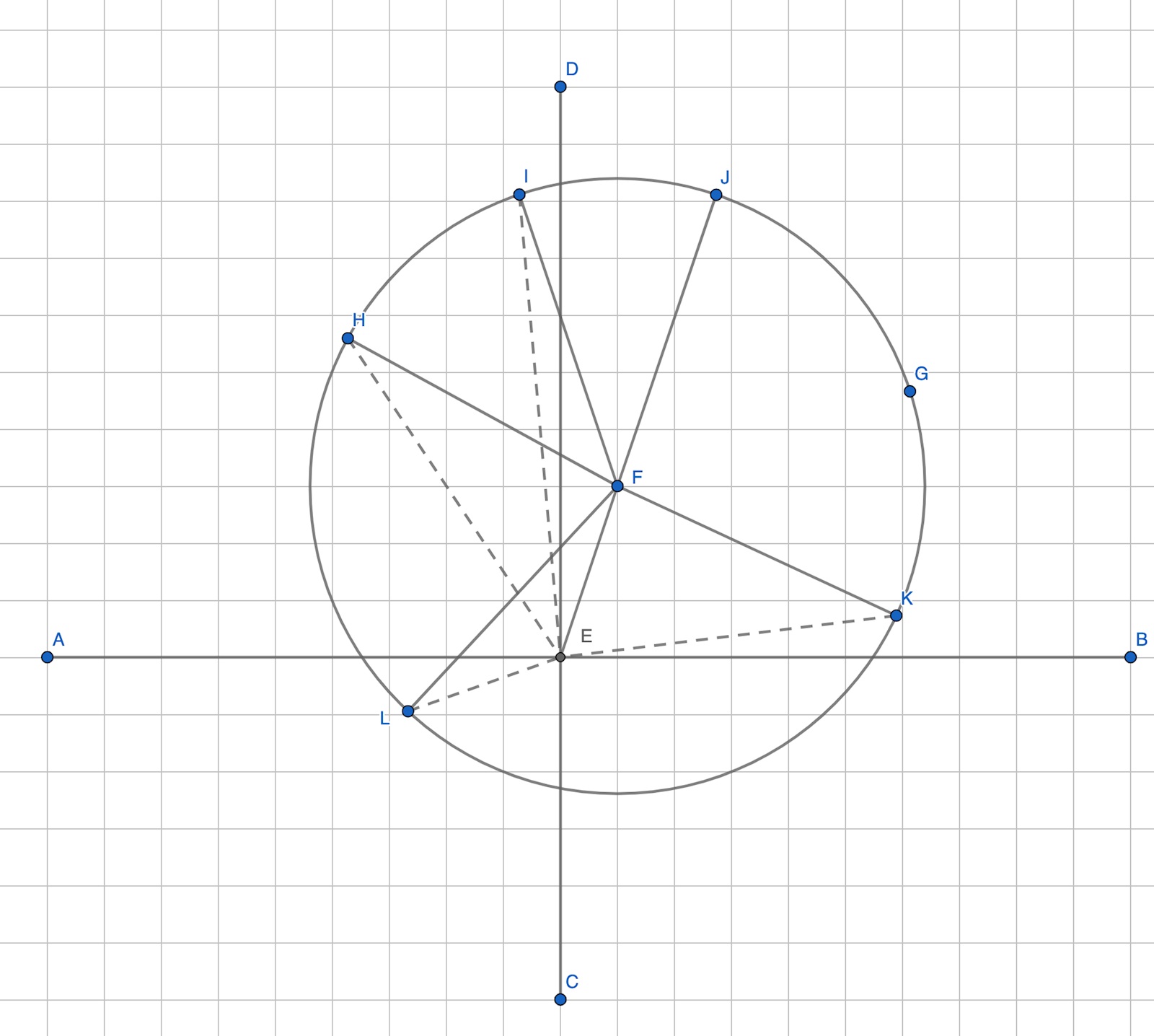
EF = z = 1+3i. Från F drag vektorn u i olika riktningar. 

VL i 

är längden av summan av vektorerna och illustreras av streckade linjer för några olika val av u i figuren ovan.

Vi vill finna det u som gör att den streckade linjen är lika lång som summan av längderna av EF och u, d.v.s. EF och cirkelns radie med centrum i F. Det är uppenbart att detta endast sker i EF:s radiella förlängning från F. Alla andra streckade linjer är kortare än sträckan EJ. Alltså är u=kz där k är något positivt reellt tal.