Hur vet vi att derivator är unika?

Du har alltså en klass funktioner F(x) sådan att D[F(x)] = f(x).

Notera att även F(x)-C där C är en konstant tillhör klassen F.

Om det finns en annan klass av funktioner G(x) sådana att D[G(x)] = f(x) har vi, då derivering är en linjär operator att

0 = f(x) - f(x) = D[F(x)]-D[G(x)] = D[F(x)-G(x)]

vilket ger

F(x)-G(x)=C

dvs.

G(x)=F(X)-C

vilket tillhör klassen F. Alltså har klassen G inte bidragit med något nytt.

(Sedan kan man skriva detta mycket snyggare och mera exakt, men i stora drag är det enligt ovan, utan att gräva ner sig i för mycket beteckningar m.m.)

Utmärkt svar, som vanligt!

Tack så mycket!

Vilka funktioner f:R\{0}—>R har derivatan f'(x)=1/x?

En matematikprofessors svar

https://m.youtube.com/watch?v=faLs3r4CE4A

Okej, så en funktion som gör jobbet är f(x)=ln(|x|). Beskriv nu samtliga funktioner f:R\{0}—>R som har derivatan f'(x)=1/x.

Ledtråd: Det finns fler primitiva funktioner än de på formen f(x)=ln(|x|)+C för C i R.

Menar du t.ex.

$\displaystyle \ln \frac{x^2}{x} + C$ ?

Nej! (Den skulle inte vara väldefinierad för x<0.)

Ny ledtråd: Kruxet här är att 1/x har en definitionsmängd som inte är sammanhängande (det finns två icke-överlappande bitar: de postiva talen och de negativa talen).

I Trinity2:s (i övrigt utmärkta!) argument antar vi implicit att definitionsmängden är sammanhängande i steget "vilket ger". Ser du hur?

Jaha, är det för att derivatan bara blir sammanhängande om domänen till ursprungsfunktionen är sammanhängande?

EDIT: jag menar alltså att Trinity bara får en derivata, alltså inget styckvis definierat. Då antar vi alltså att domänen till funktionen som deriverades också hade en helt sammanhängande domän?

Ja, nu börjar det brännas! Föreställ dig grafen till Trinity2:s funktion $f(x)=\ln(|x|)$:

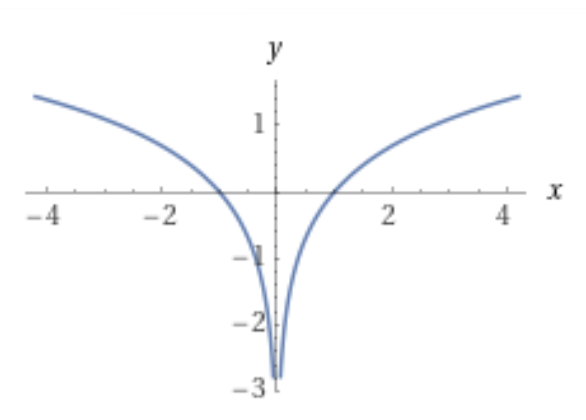
Frågan vi ska ställa oss är hur vi kan modifiera funktionen utan att derivatan ändras (eller för den delen råkar bli odefinierad!) i någon punkt. Ett uppenbart svar är att vi kan flytta hela grafen uppåt eller nedåt genom att addera en konstant $C$ på hela definiitionsmängden. Men – i och med att definitionsmängden inte är sammanhängande kan vi hantera den positiva delen och den negativa delen separat, och göra en "styckvis definierad modifiering"! 

Kan du utifrån den ledtråden skriva ner en generell formel för alla primitiva funktioner till $\frac{1}{x}$ nu?

Funkar även $\ln(D|x|)$? 

Ja, men det är samma sak som ln(|x|) + ln(D).

Right, gymnasiematten sitter inte… :D

Jag kanske bara är lite trög nu men jag förstår inte vad du vill att jag ska göra. Fångar inte $\ln |x| + C$ alla primitiva funktioner till $1/x$?

Du missar oändligt många primitiva funktioner!

Skulle du kunna ge ett exempel på en primitiv funktion som inte täcks av $\ln |x| + C$?

Nu hänger jag inte riktigt med. Är det inte det som absolutbeloppet betyder? Att den är styckvis definierad?

Jag tycker det verkar som om funktionen $\ln |x | + C$ är samma funktion som det du föreslog.

Du kan ta t.ex

ln(x) + 17, för x > 0

och

ln(-x) + 2, för x < 0

Men båda de fångas väl i $\ln|x| + C$? Eller menar ni att man kan välja två konstanter, en för varje "sida"?

Exakt! Du kan välja C och D oberoende av varandra!

Men varför är då:

$\displaystyle \int \frac{1}{x}\mathrm{d}x = \ln|x| + C$?

Det är ju det man får om man skulle slå integralen på exempelvis WolframAlpha.

Vad menar man ens när man skriver en formel i stil med "$\int f(x)\,\mathrm{d}x=F(x)+C$"?

Jag får erkänna att jag aldrig riktigt förstått vad en "obestämd integral" är för slags objekt. Är $\int f(x)\,\mathrm{d}x$ mängden av alla primitiva funktioner till $f$? Och är $F(x)+C$ i så fall en förkortning av $\{F(x)+C:C\in\mathbb{R}\}$?

Om svaret är ja på föregående frågor, så är det mycket riktigt fel att säga att $\int 1/x\,\mathrm{d}x=\{\ln(|x|)+C:C\in\mathbb{R}\}$, utan mängden ska i stället inkludera alla funktioner på den formen jag gav i #18.

Att man ändå kan hitta den felaktiga formeln med bara en kontant på diverse formelblad (och kanske rent av i WolframAlpha?) beror nog på att folk oftast vill använda de primitiva funktionerna för att beräkna bestämd integraler $\int_a^b 1/x\,\mathrm{d}x$, och detta makear bara sense om $a$ och $b$ har samma tecken, och då är bara en av konstanttermerna relevant. Men om man inte specificerar att man begränsar sig till positiva/negativa tal så är det ju fel, och borde korrigeras.

Ytterligare en faktor kan nog vara att många helt enkelt bara har memorerat "lägg till +C för att få alla primitiva funktioner", och inte är riktigt medvetna om att detta bara gäller om definitionsmängden är sammanhängande. Och det var väl lite det jag ville påminna om genom att dra upp det här exemplet, även om det kanske blev lite väl mycket av ett sidospår från din ursprungsfråga! ^_^

Nu är jag ute på lite djupt vatten här, för jag har aldrig funderat ordentligt på detta. Såvitt jag vet brukar man definiera $\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}$ som en operator med mappningen $f \mapsto f'$, och då definieras $\displaystyle \int \mathrm{d}x$ som inversoperatorn till denna. Så att:

$\displaystyle \int_{}^{}\frac{\mathrm{d}}{\mathrm{d}x}f\left(x \right)\mathrm{d}x=f\left(x \right)+C$

Men denna definition kanske, som du säger, bara håller om $f$ är sammanhängande på intervallet där den deriveras.

Så det man får ut då är en klass funktioner, inte en mängd, tror jag. Men det finns säkerligen många definitioner som inte skiljer sig åt märkvärt.

Jag måste säga att jag är HELT mindblown av detta. Jag köper argumentet och logiken du framförde här, men jag kan inte tro mina ögon. Hela min värld skakades om av det här!

Jag skulle vilja återuppliva den här tråden. Jag vet inte varför jag inte tänkte på detta när jag skrev #25 men jag tror det mest gängse sättet att definiera en obestämd integral på är:

$\displaystyle \int_{}^{}f \left(x \right)\mathrm{d}x:=\int_{t=c}^{t=x}f\left(t \right)\mathrm{d}t$

för något $c \in\mathbb{R}$ som beror på $F$. Då kan man definiera integralen utifrån Riemannsumman och slippa krångla med operatorer. Men jag vet inte vilket sätt som är bäst eller om det ens spelar någon roll hur man gör. Definitionerna förefaller vara ekvivalenta, åtminstone för enklare funktioner.

EDIT: Men den brakar såklart samman för en enkel funktion som $F(t)=\sin t + 5$

Jag tycker ni slirar lite på definitionerna av primitiv funktion :-) Så här säger till exempel Eriksson, Larsson, Wahde

Intervallet måste vara ett "äkta" intervall.

För att säkerställa att vi inte pratar förbi varandra kommer här lite förtydligande följdfrågor på de senaste inläggen i tråden!

D4NIEL skrev:

Jag tycker ni slirar lite på definitionerna av primitiv funktion :-)

Jag skulle personligen säga att en primitiv funktion till en funktion $f\colon D\to\mathbb{R}$ definierad på en öppen mängd $D\subseteq\mathbb{R}$ är en deriverbar funktion $F\colon D\to\mathbb{R}$ sådan att $F'=f$. 

Det jag funderar över är hur begreppet primitiv funktion är relaterat till det mer mystiska konceptet "obestämd integral". Vad exakt menar man när man skriver uttrycket $\int f(x)\mathrm{d}x$?

Så här säger till exempel Eriksson, Larsson, Wahde

Det där förvirrar mig väldigt mycket, med tanke på att det ju finns oändligt många primitiva funktioner till $f$. Menar de att var och en av dessa primitiva funktioner är lika med "$\int f(x)\mathrm{d}x$"? Betyder det att alla de primitiva funktionerna är lika med varandra? Blir inte det en motsägelse?

Intervallet måste vara ett "äkta" intervall.

Vad menar du med "äkta"? Att intervallet inte får vara lika med hela $\mathbb{R}$? Varför inte?

naytte skrev:

[...] jag tror det mest gängse sättet att definiera en obestämd integral på är:

$\displaystyle \int_{}^{}f \left(x \right)\mathrm{d}x:=\int_{t=c}^{t=x}f\left(t \right)\mathrm{d}t$

för något $c \in\mathbb{R}$ som beror på $F$.

Vad menar du med $F$ här? Hur menar du att $c$ ska väljas?

Men den brakar såklart samman för en enkel funktion som $F(t)=\sin t + 5$

Hur menar du här?

naytte skrev:

Så det man får ut då är en klass funktioner, inte en mängd, tror jag. 

Vad menar du med klass?

Vad menar du med $F$ här? Hur menar du att $c$ ska väljas?

Med $F$ menar jag vad integralen till vänster om definitionstecknet ger. Så den "primitiva funktionen" till $f$. Jag ska försöka illustrera vad jag menar med ett enkelt exempel:

$\displaystyle \int_{}^{}\left(2x+1 \right)\mathrm{d}x\underbrace{=}_{\text{per def}}\int_{t=c}^{t=x}\left(2t+1\right)\mathrm{d}t=x^2+x-c^2-c=x^2+x+\left(-c^2-c\right)$

"Konstanttermen" $-c^2-c$ kan vi välja till vad vi vill, och det beror ju på något begynnelsevillkor. Det är det jag menar med att $c$ "beror på" $F$. För enkla funktioner som denna kommer vi alltid kunna skapa en godtycklig konstantterm med något $c$.

Men den här definitionen brakar ju ihop för funktioner som exempelvis $F(t)=\sin t + 5$. Vi ser ju att $F'\left( t \right) = f\left( t \right) = \cos t$. Men om vi försöker bestämma den obestämda integralen av $f\left( t \right)$ med hjälp av "definitionen" jag gav ovan blir det problematiskt för då får man:

$\displaystyle \int_{}^{}\left(\cos x\right)\mathrm{d}x\underbrace{=}_{\text{per def}}\int_{t=c}^{t=x}\left(\cos t\right)\mathrm{d}t=\sin x-\sin c$

Och problemet blir ju att $-1\le \sin c\le1$, så det finns ju inget $c$ som gör att man kan skapa konstanttermen 5.

Tillägg: 17 jun 2024 20:51

Såg nu att du hade skrivit ett till inlägg. Startade just ett CS-game :/

Återkommer senare.

Ah, då förstår jag den biten av ditt inlägg!

För att parafrasera dig så är din poäng alltså att om $f:I\to\mathbb{R}$ är integrerbar på ett öppet intervall $I\subseteq\mathbb{R}$, så kan du skapa en primitiv funktion $F:I\to\mathbb{R}$ genom att välja något $c\in I$ och sedan sätta

   $F(x)=\int_c^x f(t)\mathrm{d}t,$

men vi inte nödvändigtvis bilda samtliga primitiva funktioner till $f$ på det här viset. Till exempel är $\sin(x)+5$ en primitiv funktion till $\cos(x)$, men vi kan inte bilda den genom integralkonstruktionen ovan.

Mycket observation!

Men jag tycker fortfarande inte vi har blivit klokare på vad "den obestämda integralen" $\int f(x)\mathrm{d}x$ är för något 🙂

oggih skrev:

För att säkerställa att vi inte pratar förbi varandra kommer här lite förtydligande följdfrågor på de senaste inläggen i tråden!

D4NIEL skrev:

Jag tycker ni slirar lite på definitionerna av primitiv funktion :-)

Jag skulle personligen säga att en primitiv funktion till en funktion $f\colon D\to\mathbb{R}$ definierad på en öppen mängd $D\subseteq\mathbb{R}$ är en deriverbar funktion $F\colon D\to\mathbb{R}$ sådan att $F'=f$. 

En sådan definition medför en stor mängd problem vid senare bevisföring, jag tror det är bättre att hålla sig till den vanliga definitionen som används av standardformelsamlingarna. Se till exempel Brohnstein m. fl.  eller den vanligaste svenska formelsamlingen Beta. När man läser integralkataloger och så vidare är det oftast definitionen med intervall man avser.

Det där förvirrar mig väldigt mycket, med tanke på att det ju finns oändligt många primitiva funktioner till $f$. Menar de att var och en av dessa primitiva funktioner är lika med "$\int f(x)\mathrm{d}x$"? Betyder det att alla de primitiva funktionerna är lika med varandra? Blir inte det en motsägelse?

Symbolen $\displaystyle \int f\left(x\right)\,\mathrm{d}x$ är flertydig och kan i olika sammanhang beteckna olika primitiva funktioner till $f$. Just därför kallar man ibland uttrycket obestämd integral. Det är förvisso en smula olycklig och vilseledande symbol, men av tradition skriver vi fortfarande så. Ett alternativt uttryck är $DF(x)=f(x)$ (för alla $x\in I$). Den betyder helt enkelt "en av funktionerna som uppfyller villkoret". Det här är alltså en beteckning för att beskriva primitiv funktion snarare än "integral".

Vad menar du med "äkta"? Att intervallet inte får vara lika med hela $\mathbb{R}$? Varför inte?

Mängden $\mathbb{R}\setminus\{0\}$ innehåller ett "hål" och är inte ett äkta intervall.

D4NIEL skrev:

oggih skrev:

Vad menar du med "äkta"? Att intervallet inte får vara lika med hela $\mathbb{R}$? Varför inte?

Mängden $\mathbb{R}\setminus\{0\}$ innehåller ett "hål" och är inte ett äkta intervall.

[...] jag tror det är bättre att hålla sig till den vanliga definitionen som används av standardformelsamlingarna. Se till exempel Brohnstein m. fl.  eller den vanligaste svenska formelsamlingen Beta. När man läser integralkataloger och så vidare är det oftast definitionen med intervall man avser.

Okej, då tror jag jag förstår. Du tycker alltså att begreppet "primitiv funktion" endast ska användas för funktioner som är definierade på (öppna) intervall, dvs. mängder av typen $(a,b)$ där $a<>$ och $a,b\in\mathbb{R}\cup\{\pm\infty\}$, medan jag tycker att man kan använda det för funktioner där definitionsmängden är en godtycklig öppen delmängd $D\subseteq\mathbb{R}$. 

Jag kan hålla med dig om att teorin blir lite renare om man håller sig till intervall (och det är nog därför som många läroböcker håller sig till det scenariot), men jag tycker det känns lite otillfredställande att inte ha ett ord för relationen mellan funktionen i #18 och $1/x$. Men jag antar att det är en smaksak! 🤷

D4NIEL skrev:

oggih skrev:

[Den där definitionen] förvirrar mig väldigt mycket, med tanke på att det ju finns oändligt många primitiva funktioner till $f$. Menar de att var och en av dessa primitiva funktioner är lika med "$\int f(x)\mathrm{d}x$"? Betyder det att alla de primitiva funktionerna är lika med varandra? Blir inte det en motsägelse?

Symbolen $\displaystyle \int f\left(x\right)\,\mathrm{d}x$ är flertydig och kan i olika sammanhang beteckna olika primitiva funktioner till $f$. Just därför kallar man ibland uttrycket obestämd integral. Det är förvisso en smula olycklig och vilseledande symbol, men av tradition skriver vi fortfarande så. Ett alternativt uttryck är $DF(x)=f(x)$ (för alla $x\in I$). Den betyder helt enkelt "en av funktionerna som uppfyller villkoret". Det här är alltså en beteckning för att beskriva primitiv funktion snarare än "integral".

Det ungefär den bilden jag har av hur obestämd-integral-symbolen används också. Men jag skulle gå längre än dig, genom säga att det är mer en en smula olyckligt att vi har den här traditionen. Det går ju verkligen verkligen helt stick i stäv mot hur vi i i stort sett alla andra matematikundervisningssammanhang trycker väldigt hårt på att studenterna ska uttrycka sig precist, och använda likhetstecknet på ett korrekt sätt.

Jag propagerar därför för följande reform:

(a) I väldigt många sammanhang (särskilt på gymnasiet) klarar man sig utan att över huvud taget använda en obestämd-integral-symbol, utan kan lika gärna säga i klarspråk precis vad man menar. Till exempel: I stället för att skriva "$\int 2x\,\mathrm{d}x=x^2+C$" kan man skriva "de primitiva funktionerna till $2x$ är $x^2+C$ för reella tal $C$".

(b) Om man nu tvunget ska använda obestämd-integral-symbolen, så bör vi en gång för alla definiera $\int f(x)\,\mathrm{d}x$ som mängden av alla primitiva funktioner till $f(x)$. Korrekt blir då att skriva

      $\displaystyle\int 2x\,\mathrm{d}x={\{x^2+C:C\in\mathbb{R}\}}$

i stället för det oklara "$\int 2x\,\mathrm{d}x=x^2+C$".

I samma veva skulle man kunna introducera något skrivsätt för $\{g(x)+C:C\in\mathbb{R}\}$, t.ex. $[g(x)]$ (på samma sätt som man ofta skriver $[m]$ för $\{m+kn:k\in\mathbb{Z}\}$ när man håller på med aritmetik modulo $n$), så att man, om man vill, kan skriva

   $\displaystyle\int 2x\,\mathrm{d}x={[x^2]}$.

Angående din punkt (b):

Jag tror till och med att man gör det redan. Återigen vet jag inte hur jag inte kom att tänka på detta när jag skrev #25 för någon vecka sedan, men i en mattelåt jag har haft på hjärnan i tre år sjungs det:

[...] und das unbestimmte Integral von f(x) dx ist die Menge aller Stammfunktionen, deren Ableitung f(x) ergibt [...]

Översatt: den obestämda integralen av f(x) dx är mängden av alla primitiva funktioner, vars derivata är f(x).

naytte skrev:

Angående din punkt (b):

Jag tror till och med att man gör det redan. Återigen vet jag inte hur jag inte kom att tänka på detta när jag skrev #25 för någon vecka sedan, men i en mattelåt jag har haft på hjärnan i tre år sjungs det:

[...] und das unbestimmte Integral von f(x) dx ist die Menge aller Stammfunktionen, deren Ableitung f(x) ergibt [...]

Översatt: den obestämda integralen av f(x) dx är mängden av alla primitiva funktioner, vars derivata är f(x).

Guldstjärna från oggih till den låtskrivaren! ^_^

Med risk för att jag kommer ångra mig (om jag också får låten på hjärnan i tre år): har du en länk till låten? 

https://www.youtube.com/watch?v=KUCG117tA20

Av kingen DorFuchs. Hade inte kommit ihåg additionsformlerna utan honom! :D

Har suttit många prov med trigonometri och nynnat hans låtar i huvudet. Då behöver man inte kunna något.

Wow, vilken underbart nördig musikalisk guldgruva! Kul sätt att öva tyska, dessutom! ^_^

Japp, verkligen. Han har en klassiker om pq-formeln som halva Tysklands befolkning har hört vid det här laget:

https://www.youtube.com/watch?v=tRblwTsX6hQ

Detta har varit min go-to Eselsbrücke (minneskrok) för att komma ihåg pq-formeln :)

Angående att konstanten bara gäller "lokalt" för funktionen, så kanske man skulle kunna lägga till sitt $+C$ som en funktion av $x$. Låt säga att vi har en funktion $f: \mathbb{R}\setminus\{ 0 \}\to\mathbb{R}$:

$\displaystyle \int_{}^{}f\left(x\right)\mathrm{d}x=F\left(x\right)+C\left(x\right)$

Där $C(x)$ är en konstant som beror på var i domänen till $f$ vi befinner oss:

$\displaystyle C{(x)}=\left\{\begin{array}{ll}A&\text{om }x>0\\B&\text{om }x<0\end{array}\right.$

Vad tror ni om det? Har vi löst vårt "problem" då?

Om vi återvänder till den ursprungliga frågan om hur vi kan veta att derivator är unika, så lär det framgå av alla inläggen att så är fallet betr de elementära fknerna som frågan gällde. Jag skulle drista mig att säga att det gäller alla deriverbara fkner f:R-->R alt. f:C-->C. Skälet är att derivator är definierade som gränsvärden och R (och C) har den egenskapen att två skilda punkter kan separeras med disjunkta omgivningar. Rum med den egenskapen kallas Hausdorff. Går vi utanför dessa så kan t ex en följd ha TVÅ olika riktiga gränsvärden - alltså inte bara hopningspunkter (för sådana kan man ha tretton på dussinet av även i R och C). Ty om två punkter inte kan separeras med öppna mängder, så kommer alltså alla omgivningar att innehålla de två punkterna. Om vi då har en följd som är konvergent så säger definitionen på konvergens att varje omgivning innehåller alla element ur följden utom ändligt många. Svaret på frågan blir då Nej.

naytte skrev:

Angående att konstanten bara gäller "lokalt" för funktionen, så kanske man skulle kunna lägga till sitt $+C$ som en funktion av $x$. Låt säga att vi har en funktion $f: \mathbb{R}\setminus\{ 0 \}\to\mathbb{R}$:

$\displaystyle \int_{}^{}f\left(x\right)\mathrm{d}x=F\left(x\right)+C\left(x\right)$

Där $C(x)$ är en konstant som beror på var i domänen till $f$ vi befinner oss:

$\displaystyle C{(x)}=\left\{\begin{array}{ll}A&\text{om }x>0\\B&\text{om }x<0\end{array}\right.$

Vad tror ni om det? Har vi löst vårt "problem" då?

Det tycker jag är en utmärkt lösning!

Om $f\colon D\to\mathbb{R}$ är en funktion definierad på en öppen mängd $D\subseteq\mathbb{R}$ och $F\colon D\to\mathbb{R}$ är en primitiv funktion, så kommer mängden av alla primitiva funktioner bestå av funktionerna $F+C$ för funktioner $C\colon D\to\mathbb{R}$ med egenskapen att $C'(x)=0$ för alla $x\in D$.

Detta villkor på $C$ motsvaras precis av att $C$ är "lokalt konstant" i bemärkelsen att den antar ett konstant värde på varje sammanhängande delintervall av definitionsmängden.

Tomten skrev:

Om vi återvänder till den ursprungliga frågan om hur vi kan veta att derivator är unika, så lär det framgå av alla inläggen att så är fallet betr de elementära fknerna som frågan gällde. Jag skulle drista mig att säga att det gäller alla deriverbara fkner f:R-->R alt. f:C-->C. Skälet är att derivator är definierade som gränsvärden och R (och C) har den egenskapen att två skilda punkter kan separeras med disjunkta omgivningar. Rum med den egenskapen kallas Hausdorff. Går vi utanför dessa så kan t ex en följd ha TVÅ olika riktiga gränsvärden - alltså inte bara hopningspunkter (för sådana kan man ha tretton på dussinet av även i R och C). Ty om två punkter inte kan separeras med öppna mängder, så kommer alltså alla omgivningar att innehålla de två punkterna. Om vi då har en följd som är konvergent så säger definitionen på konvergens att varje omgivning innehåller alla element ur följden utom ändligt många. Svaret på frågan blir då Nej.

Det jag uppfattar att naytte frågade i sitt urprungsinlägg är om primitiva funktioner alltid är unika, i bemärkelsen att om du har en primitiv funktion, så får du samtliga genom att bara lägga till en konstant (eller en "lokalt konstant funktion", som vi under trådens gång har förfinat det till). 

Det jag uppfattar att du svarar på här är en delvis annan fråga (som mer hänger ihop med titeln på tråden), nämligen huruvida derivatan är väldefinierad, i bemärkelsen att följande gränsvärde är unikt för varje $x$ där det existerar:

   $f'{(x)}=\displaystyle\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}.$

Precis som du säger följer detta av ett mer generellt faktum: en reell funktion tal har alltid maximalt ett gränsvärde när variabeln går mot ett visst värde. Man kan visa det med triangelolikheten (eller mer abstrakt hänvisa till Hausdorff-egenskapen hos de reella talen, om man har läst en kurs i topologi på universitetet). Jag frågade faktiskt själv om detta på PA för många herrans år sedan! ^_^

Det vanligaste användningsområdet för obestämda integraler är att på ett givet intervall $I$ använda en och endast en konstant, inte att byta mellan olika konstanter. Låt $I$ vara det slutna intervallet $[0,\pi/4]$ och studera den bestämda integralen

$\displaystyle \int_0^{\pi/4}\frac{2\sin\left(x\right)}{\cos^3\left(x\right)}\,\mathrm{d}x$

Uppenbarligen gäller

$\displaystyle \int\frac{2\sin\left(x\right)}{\cos^3\left(x\right)}\,\mathrm{d}x=\tan^2\left(x\right)\text{ och }\int\frac{2\sin\left(x\right)}{\cos^3\left(x\right)}\,\mathrm{d}x=\frac{1}{\cos^2(x)}$

Eftersom symbolen för obestämd integral inte är entydig kan vi därav inte dra slutsatsen att $\frac{1}{\cos^2(x)}=\tan^2\left(x\right)$. Däremot kan vi använda integralkalkylens fundamentalsats och beräkna den sökta integralen över $I$ med vilken som helst av våra primitiva funktioner:

$\displaystyle \int_0^{\pi/4}\frac{2\sin\left(x\right)}{\cos^3\left(x\right)}\,\mathrm{d}x=F\left(\pi/4\right)-F\left(0\right)=\tan^2 \left(\pi/4\right)-\tan^2\left(0\right)=\frac{1}{\cos^2(\pi/4)}-\frac{1}{\cos^2(0)}=1$

Men vi får vi inte byta konstant $C(x)$ mitt i beräkningen, trots att vi är vid olika värden på $x$.

$\displaystyle \int_0^{\pi/4}\frac{2\sin\left(x\right)}{\cos^3\left(x\right)}\,\mathrm{d}x\neq \tan^2\left(\pi/4\right)-\frac{1}{\cos^2(0)}=0$

Jag är därför lite tveksam till den praktiska nyttan av att frångå gängse definitioner.  Dessutom känns en "konstant" som en funktion av $x$ lite krystat i just det här fallet även om jag förstår att det är roligt :-)

Fast "konstantfunktionen" $C:D\to\mathbb{R}$ ska ju ha egenskapen att $C^\prime(x)=0$ för alla $x\in D$, så $C$ måste vara konstant på varje intervall som ingår i definitionsmängden.

Så i fallet där integranden är $2\sin(x)/\cos^3(x)$ så vi vi inte byta värde mellan $0$ och $\pi/4$.

Men ja, eftersom bestämda integraler (i princip) bara makear sense över intervall som är helt inkluderade i definitionsmängden, så håller jag med om att min käpphäst med att man kan välja olika konstanter på disjunkta delintervall av definitionsmängden är irrelevant för att beräkna bestämda integraler!

Sen tycker jag ändå att problemet "bestäm mängden av alla funktioner som har en viss derivata" är fundamentalt nog för att vara intressant av ren nyfikenhet, även för funktioner med hål i definitionsmängden! ^_^

Nu är jag lite förvirrad över vad som hände här. Varför skulle vi vara tvungna att byta konstant i intervallet $[0, \pi/4]$? Konstanten kommer väl vara densamma över hela intervallet, eftersom integranden är sammanhängande på det?

Jag antar att det var det du påpekade, oggih?

Exakt! Bestämda integraler beräknas alltid över intervall $I\subseteq\mathbb{R}$ (som per definition är sammanhängande!), och en funktion $C:I\to\mathbb{R}$ med egenskapen att $C^\prime(x)=0$ för alla $x\in I$ kommer automatiskt att vara konstant.

Båda funktionerna $\tan^2(x)$ och $\frac{1}{\cos^2(x)}$ är primitiva funktioner. Det enda som skiljer dem åt är en konstant.

Jag har svårt att koppla ihop det med er beteckning

$\displaystyle \int f\left(x\right)\mathrm{d}x=F\left(x\right)+C\left(x\right)$

Jag antar att $F(x)$ är någon av funktionerna, men konstanten $C$ måste av någon anledning vara en funktion av $x$ för att?

Det känns som att ni har hittat på en helt egen definition av primitiv funktion och sedan hittar ni på ytterligare en konstruktion för att få använda den bakvända definitionen :-)

Det är muntert att titta in och se den här diskussionen - på midsommarafton! Det är vad jag kallar engagemang. :)

Trevlig midsommar!

Jag tror vi pratar förbi varandra lite. Här kommer ett försök att förtydliga vad jag menar:

Fört av allt: Den fundamentala frågan som naytte ställde i sitt ursprungsinlägg handlade (formulerat i mina ord!) om att bestämma mängden av samtliga funktioner som har en viss given derivata $f$, eller annorlunda uttryckt: mängden av alla primitiva funktioner till $f$, i följande bemärkelse (där vi följer Wikipedias definition):

Definition. Låt $f\colon D\to\mathbb{R}$ vara en funktion definierad på en öppen mängd $D\subseteq\mathbb{R}$. En primitiv funktion till $f$ är en funktion $F\colon D\to\mathbb{R}$ sådan att $F^\prime(x)=f(x)$ för alla $x\in D$.

Påståendet som jag för fram i tråden är detta:

Sats. Låt $F\colon D\to\mathbb{R}$ vara en primitiv funktion till en funktion $f\colon D\to\mathbb{R}$. Då är $G\colon D\to\mathbb{R}$ en primitiv funktion till $f$ om och bara om $G=F+C$ för någon lokalt kontant funktion $C\colon D\to\mathbb{R}$ (alltså en funktion som uppfyller $C^\prime(x)=0$ för alla $x\in D$).

Notera att varje öppen delmängd $D\subseteq\mathbb{R}$ kan skrivas som en union av disjunkta öppna intervall (dessa kan vara begränsade eller obegränsade), och att en funktion $C\colon D\to\mathbb{R}$ är lokalt konstant om och bara om den är konstant på varje sådant disjunkt öppet delintervall. Som har påpekats ovan kan konstanterna på de olika delintervallen väljas oberoende av varandra, vilket även Wikipedia påpekar.

Om $D$ däremot är sammanhängande (och alltså består av ett enda intervall) så är "lokalt konstant" samma sak som "konstant", och vi får följande välkända resultat som följdsats:

Korollarium. Låt $F\colon D\to\mathbb{R}$ vara en primitiv funktion till en funktion $f\colon D\to\mathbb{R}$ definierad på ett intervall. Då är $\colon D\to\mathbb{R}$ en primitiv funktion till $f$ om och bara om $G=F+C$ för någon kontant $C\in\mathbb{R}$.

Tillägg: 21 jun 2024 16:55

Trevlig midsommar alla! 🌼

oggih skrev:

(där vi följer Wikipedias definition):

Wikipedia ger inte någon definition. Däremot ger artikeln två källhänvisningar. När vi granskar källorna som Wikipedia hänvisar till ser det ut så här:

[1] Stewart, James (2008). Calculus: Early Transcendentals (6th ed.). Brooks/Cole. ISBN 978-0-495-01166-8.

[2] Larson, Ron; Edwards, Bruce H. (2009). Calculus (9th ed.). Brooks/Cole. ISBN 978-0-547-16702-2.

Vad gäller hur vi använder begreppet i Sverige vet jag att det ser likartat ut även vid SU/KTH och Linköpings- och Lunds universitet. (Eftersom jag redan nämnt standardverk som FEG, Beta mfl och jag inte ska vara alltför lokalpatriotisk tar vi för rättvisans skull upp Persson Böiers Inledande analys i en variabel):

Självklart går det att definiera primitiv funktion på det oortodoxa vis ni vill göra, men det introducerar praktiska problem vid formulering och/eller bevis av senare satser, något som till exempel Folland påpekar under kapitlet om Choquet. Bland visar Folland att en funktion $f$ endast har en primitiv funktion om man kan upprätta en bijektiv kontinuerlig funktion $\phi$ så att $f\circ \phi$ är Baire 1 (och uppfyller medelvärdessatsen). Problem uppstår om vi tillåts skapa illvilliga hål i intervallen och använda öppna mängder. Jag håller alltså inte alls med om att den definition du föreslår skulle vara vanlig  (eller den mest genomtänkta).

I tabellverk över integraler använder man ofta beloppstecknet. Har den kontinuerliga funktionen

$f(x)=|x|$

någon primitiv funktion?

D4NIEL skrev:

Wikipedia ger inte någon definition. 

Det jag syftar på är första meningen i Wikipedia-artikeln, som säger att en primitiv funktion till en funktion $f$ är en funktion $F$ med $F'=f$, utan att kräva att definitionsmängden för $f$ ska vara ett intervall. Tvärtom påpekar artikeln senare att man kan välja olika konstanter på varje disjunkt delintervall av en icke-sammanhängande definitionsmängd, och ger $f:\mathbb{R}\setminus\{0\}\to\mathbb{R}$ med $f(x)=1/x^2$ som ett exempel.

Av detta tycker jag det är tydligt att Wikipedia ansluter sig till mitt synsätt, dvs. att det är meningsfullt att tala om primitiva funktioner även för funktioner med icke-sammanhängande definitionsmängd. Detta menar jag i sin tur visar att detta synsätt är någorlunda allmänt accepterat i matematikvärlden – även om det som du har visat finns ett stort antal läroböcker som väljer att enbart diskutera primitiver för funktioner med sammanhängande definitionsmängd.

D4NIEL skrev:

Självklart går det att definiera primitiv funktion på det oortodoxa vis ni vill göra, men det introducerar praktiska problem vid formulering och/eller bevis av senare satser, något som till exempel Folland påpekar under kapitlet om Choquet. Bland visar Folland att en funktion $f$ endast har en primitiv funktion om man kan upprätta en bijektiv kontinuerlig funktion $\phi$ så att $f\circ \phi$ är Baire 1 (och uppfyller medelvärdessatsen). Problem uppstår om vi tillåts skapa illvilliga hål i intervallen och använda öppna mängder. 

Kan du utveckla vilken slags problem det skapar?

I just fallet med den satsen du beskriver, så tänker jag att vi måste beskriva vad $f$ och $\phi$ har för definitionsmängder för att göra påståendet precist, och då kommer vi behöva specificera att definitionsmängden för $f$ är sammanhängande – oavsett om vi jobbar med min bredare definition eller din snävare definition av begreppet "primitiv funktion" – t.ex. så här:

Sats. Om en funktion $f:I\to\mathbb{R}$ definierad på ett öppet intervall $I\subseteq\mathbb{R}$ har en primitiv funktion, så existerar det en kontinuerlig bijektion $\phi:I\to I$ sådan att $f\circ\phi$ är Baire 1.

Men jag kanske missförstår vilket problem du har i åtanke?

D4NIEL skrev:

I tabellverk över integraler använder man ofta beloppstecknet. Har den kontinuerliga funktionen

$f(x)=|x|$ någon primitiv funktion?

Jag skulle säga att en funktion $F:\mathbb{R}\to\mathbb{R}$ är en primitiv funktion till $f:\mathbb{R}\to\mathbb{R}$ med $f(x)=|x|$ om och bara om den ges av

   ${F(x)}=\left\{\begin{array}{ll}\frac{1}{2}x^2+C&\text{om $x\geq 0$}\\-\frac{1}{2}x^2+C&\text{om $x<0$}\end{array}\right.$

för någon konstant $C\in\mathbb{R}$. Håller du med?

D4NIEL skrev: Jag håller alltså inte alls med om att den definition du föreslår skulle vara vanlig  (eller den mest genomtänkta).

Har du något annat förslag på vad vi ska kalla funktionerna $F:\mathbb{R}\setminus\{0\}\to\mathbb{R}$ på formen

   $F{(x)}=\left\{\begin{array}{ll}\ln(x)+C&\text{om }x>0\\\ln(-x)+D&\text{om }x<0\end{array}\right.$

för $C,D\in\mathbb{R}$, i förhållande till funktionen $f:\mathbb{R}\setminus\{0\}\to\mathbb{R}$ med $f(x)=1/x$, i stället för "primitiva funktioner"? 🙂

https://www.pluggakuten.se/trad/plotslig-fundering-vilken-sats-sager-att-en-primitiv-funktion-derivata-alltid-ar-entydlig/

Haha!

naytte skrev:

Nu är jag ute på lite djupt vatten här, för jag har aldrig funderat ordentligt på detta. Såvitt jag vet brukar man definiera $\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}$ som en operator med mappningen $f \mapsto f'$, och då definieras $\displaystyle \int \mathrm{d}x$ som inversoperatorn till denna. Så att:

$\displaystyle \int_{}^{}\frac{\mathrm{d}}{\mathrm{d}x}f\left(x \right)\mathrm{d}x=f\left(x \right)+C$

Men denna definition kanske, som du säger, bara håller om $f$ är sammanhängande på intervallet där den deriveras.

Så det man får ut då är en klass funktioner, inte en mängd, tror jag. Men det finns säkerligen många definitioner som inte skiljer sig åt märkvärt.

---

Jag måste säga att jag är HELT mindblown av detta. Jag köper argumentet och logiken du framförde här, men jag kan inte tro mina ögon. Hela min värld skakades om av det här!

Vad var din konceptuella förståelse av den obestämda integralen i ditt liv _före_ den här tråden, eftersom du beskriver tråden lite som ett paradigmskifte i ditt medvetande?

Jag frågar _inte_ ironiskt, utan av genuin nyfikenhet, då jag personligen tycker det mest intressanta är hur man tar till sig och uppfattar nya begrepp, och kanske inte är riktigt lika fixerad vid dess exakta definitioner.

Jag kan tex avslöja att min förståelse för begreppet är ungefär den som Oggih beskriver, dvs att jag aldrig riktigt har förstått meningen med begreppet obestämd integral, och därför kanske inte heller brytt mig så mycket om den. (Inom ingenjörsvärlden klarar man sig ganska långt med integralkalkylens huvudsats och funktioner som är hyfsat väldefinierade inom det intervall man är intresserad av).   

För övrigt ligger Dorfuchs numera på min spotify-spellista🤘  

Vad var din konceptuella förståelse av den obestämda integralen i ditt liv _före_ den här tråden, eftersom du beskriver tråden lite som ett paradigmskifte i ditt medvetande?

Jag hade någon uppfattning om att obestämda integraler på något sätt skulle fånga alla "primitiva funktioner" till en integrand. 

Det som var förvänande eller ögonöppnande för mig var just det Oggih påpekade, att en funktion definierad på en öppen mängd $D\subset \mathbb{R}$ med ett (eller flera) hål, och alltså har en icke-sammanhängande domän, måste behandlas annorlunda än funktioner med helt sammanhängande domäner. Exemplet nedan är särskilt relevant:

$\displaystyle \int \frac{1}{x}\mathrm{d}x$ 

Under hela min gymnasietid har jag indoktrinerats med mantrat "integralen av 1/x är ln av beloppet av $x$ + C", dels av folk på YouTube, Instagram och andra sociala medier, och dels av exempelvis min gymnasielärare i matematik. Att då helt plötsligt få reda på att man har haft fel om integralen till en sådan fundamental funktion, och dessutom att det var vad man ansåg vara matematiska auktoriteter som förmedlade den här felaktigeten, är, som du kanske förstår, ytterst förvånande.

(Inom ingenjörsvärlden klarar man sig ganska långt med integralkalkylens huvudsats och funktioner som är hyfsat väldefinierade inom det intervall man är intresserad av)

Det här är något jag har funderat en del på. Man kan väl inte integrera med analysens fundamentalsats utan att först veta vad en obestämd integral är? Den vanliga (och kanske lite naiva) metoden är ju med hjälp av gränsvärden av Riemannsummor, men utan att veta vad en obestämd integral är, förstår jag inte hur man kan komma vidare med den definitionen. 

Vänta lite, jag har en fundering här. Konstruktionen du presenterar Oggih känns konstig eller typ malicious. Man kan styckvis skifta den primitiva funktionen mellan hål i ursprungsfunktionens domän som i fallet 1/x, yes. Men hade jag varit guden av matematik hade jag patchat din konstruktion för punkthål genom att postulera att primitiva funktionen måste anta sitt gränsvärde i ett punkthål om den existerar och om derivatan som då går att beräkna i punkten sammanfaller med ursprungsfunktionens gränsvärde där. Jag tillåter alltså att primitiva funktionen har större domän än urspr funktionen, är det några problem med det?

Du och dina counter examples!!!

På tal om det naytte, så kan du kolla in boken counter examples in analysis. Om du tyckte att Oggihs grej här var upplysande så finns det hundratals upplysningar som väntar på dig där. De jag minns bäst personligen är 

• Weierstrassfunktionen
• En funktion som är slät i en punkt och har derivata noll av ALLA ordningar där, men är inte nollfunktionen.

naytte skrev:

Vad var din konceptuella förståelse av den obestämda integralen i ditt liv _före_ den här tråden, eftersom du beskriver tråden lite som ett paradigmskifte i ditt medvetande?

Jag hade någon uppfattning om att obestämda integraler på något sätt skulle fånga alla "primitiva funktioner" till en integrand. 

Det som var förvänande eller ögonöppnande för mig var just det Oggih påpekade, att en funktion definierad på en öppen mängd $D\subset \mathbb{R}$ med ett (eller flera) hål, och alltså har en icke-sammanhängande domän, måste behandlas annorlunda än funktioner med helt sammanhängande domäner. Exemplet nedan är särskilt relevant:

$\displaystyle \int \frac{1}{x}\mathrm{d}x$ 

Under hela min gymnasietid har jag indoktrinerats med mantrat "integralen av 1/x är ln av beloppet av $x$ + C", dels av folk på YouTube, Instagram och andra sociala medier, och dels av exempelvis min gymnasielärare i matematik. Att då helt plötsligt få reda på att man har haft fel om integralen till en sådan fundamental funktion, och dessutom att det var vad man ansåg vara matematiska auktoriteter som förmedlade den här felaktigeten, är, som du kanske förstår, ytterst förvånande.

Jo, jag förstår dig. Men så är det ju, att ju mer man grottar ner sig i detaljer, desto mindre tid får man över för att bekanta sig med koncepten (om man ens då lyckas se konceptet mär alla detaljer är ivägen). Man sållar bort detaljer ganska friskt på gymnasiet i alla naturveteskapliga ämnen, matte inkluderat. 

(Inom ingenjörsvärlden klarar man sig ganska långt med integralkalkylens huvudsats och funktioner som är hyfsat väldefinierade inom det intervall man är intresserad av)

Det här är något jag har funderat en del på. Man kan väl inte integrera med analysens fundamentalsats utan att först veta vad en obestämd integral är? Den vanliga (och kanske lite naiva) metoden är ju med hjälp av gränsvärden av Riemannsummor, men utan att veta vad en obestämd integral är, förstår jag inte hur man kan komma vidare med den definitionen. 

Det jag menade var att om man i ingenjörsvärlden får sådana hål i definitionsmängder beror det oftast på brister i den matematiska modelleringen av verkligheten. Och då måste det ändå hanteras på något sätt.  

Det jag menade var att om man i ingenjörsvärlden får sådana hål i definitionsmängder beror det oftast på brister i den matematiska modelleringen av verkligheten. Och då måste det ändå hanteras på något sätt. 

Jag tror du missförstod mig. Min fråga är: hur kan man ens motivera analysens fundamentalsats utan att känna till obestämda integraler? Det finns t.ex. härledningar som bygger på medelvärdessatsen, men det verkar som man redan måste veta vad en integral är för att sådana härledningar ska vara meningsfulla.

Jag tror att JohanF menar att ingenjörer accepterar algebrans fundamentalsats utan bevis och använder den i sina beräkningar. Bevisandet överlåter vi till matematikerna.

Jag skulle hävda att man inte riktigt behöver konceptet obestämd integral vare sig för att bevisa eller använda analysens huvudsats. Det man behöver är konceptet bestämd integral (definierad via t.ex. Riemann-summor) och konceptet primitiv funktion (där den oenighet vi har sett i tråden inte spelar någon roll, eftersom bestämda integraler definieras på intervall).

Både Smaragdalena och Oggih tillsammans svarade på frågan du ställde till mig.

Ingenjörer i allmänhet använder nog allt som funkar och tänker mer sällan på varför det funkar (förutom på någon slags konceptuell nivå naturligtvis). Jag vill gärna också veta vad ovanstående får för konsekvenser i gymnasiepraktiken, så jag är kanske inte en genomsnittlig ingenjör...

Som jag förstår (men jag kan ha fel), så får detta aldrig någon konsekvens på den formel man normalt använder på gymnasiet, dvs

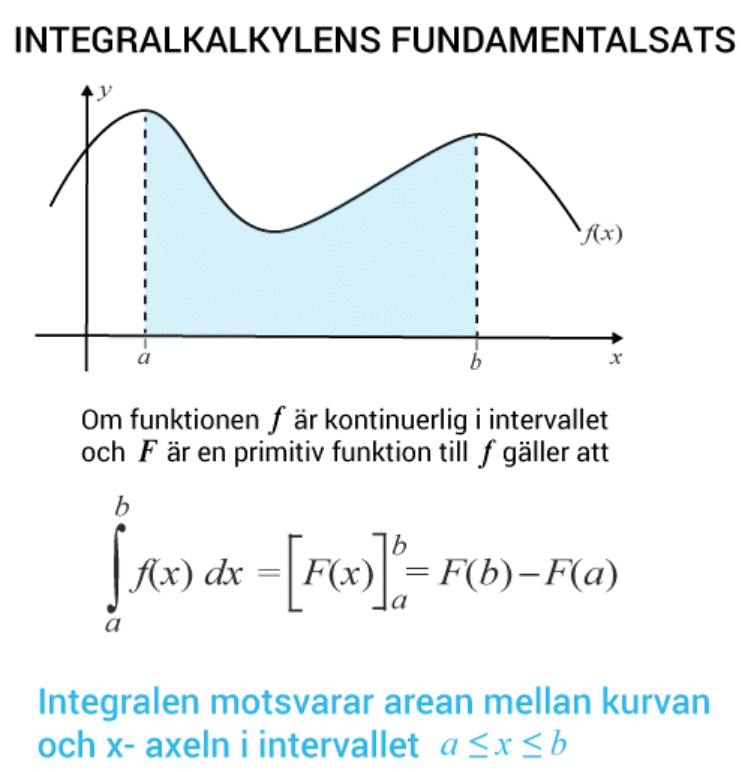
Däremot blir det problem om funktionen f har hål som är odefinierade. Men det blir mer problem än just problemet som berörs i tråden (dvs att konstanten C nödvändigtvis inte kancelleras, eftersom det kan vara olika konstanter). 

Så jag tänker mig att en typisk "gymnasiereflektion" skulle vara att:

"Ojdå, man kan ju inte räkna ut en area av något som är odefinierat så då kan inte heller formeln gälla"

och sedan går man vidare lika glad (och omedveten) som man var innan. Det är inte speciellt många gymnasieelever som ligger på den avancerade reflektionsnivå som du gör.

oggih skrev:

Jag skulle hävda att man inte riktigt behöver konceptet obestämd integral vare sig för att bevisa eller använda analysens huvudsats. Det man behöver är konceptet bestämd integral (definierad via t.ex. Riemann-summor) och konceptet primitiv funktion (där den oenighet vi har sett i tråden inte spelar någon roll, eftersom bestämda integraler definieras på intervall).

Hm. Jag har ett förslag på en vanlig härledning med gränsvärden. Skulle du säga att man klarar sig utan ett ordentligt begrepp om "obestämda integraler" även här?:

Låt $f:D\to \mathbb{R}, D\subseteq \mathbb{R}$ vara en på sin definitionsmängd kontinuerlig funktion.  Skapa en areaberäknande funktion till $f$ enligt $x \mapsto A\left( x \right)$, som beräknar arean på $[0, x]$. Arean mellan $x$ och $x+h$ kan då beräknas med $A(x+h)-A(x)$. Vi kan se att:

$\displaystyle hf\left(x\right)\le A\left(x+h\right)-A\left(x\right)\le hf(x+h)$

Om vi klämmer på ett gränsvärde och låter $h\to 0$ ser vi med hjälp av klämsatsen att:

$\displaystyle A'\left(x\right)=\frac{A\left(x+h\right)-A\left(x\right)}{h}=f\left(x\right)$

Nu är det sista steget att integrera. I mitt huvud krävs här obestämda integraler. Lösningen på differentialekvationen vill vi väl trots allt ska vara heltäckande på något sätt?

naytte skrev:

oggih skrev:

Jag skulle hävda att man inte riktigt behöver konceptet obestämd integral vare sig för att bevisa eller använda analysens huvudsats. Det man behöver är konceptet bestämd integral (definierad via t.ex. Riemann-summor) och konceptet primitiv funktion (där den oenighet vi har sett i tråden inte spelar någon roll, eftersom bestämda integraler definieras på intervall).

Hm. Jag har ett förslag på en vanlig härledning med gränsvärden. Skulle du säga att man klarar sig utan ett ordentligt begrepp om "obestämda integraler" även här?:

Låt $f:D\to \mathbb{R}, D\subseteq \mathbb{R}$ vara en på sin definitionsmängd kontinuerlig funktion.  Skapa en areaberäknande funktion till $f$ enligt $x \mapsto A\left( x \right)$, som beräknar arean på $[0, x]$. Arean mellan $x$ och $x+h$ kan då beräknas med $A(x+h)-A(x)$. Vi kan se att:

$\displaystyle hf\left(x\right)\le A\left(x+h\right)-A\left(x\right)\le hf(x+h)$

Om vi klämmer på ett gränsvärde och låter $h\to 0$ ser vi med hjälp av klämsatsen att:

$\displaystyle A'\left(x\right)=\frac{A\left(x+h\right)-A\left(x\right)}{h}=f\left(x\right)$

Nu är det sista steget att integrera. I mitt huvud krävs här obestämda integraler. Lösnings på differentialekvationen vill vi väl trots allt ska vara heltäckande på något sätt?

Jag skulle säga att för att slutföra beviset behöver man bara hitta _en_ primitiv funktion i intervallet, för att sedan kunna skriva den sökta arean i intervallet som en differens mellan två areor.

Men så är jag inte matematiker heller ;-)

Men så är jag inte matematiker heller ;-)

Jag har doodlat lite nu och du har nog rätt. Man behöver nog bara hitta en primitiv funktion som uppfyller vissa villkor. Jag har försökt formulera resonemanget på ett så "allmänt" sätt som möjligt, men någon får gärna inflika om jag gör icke-generella antaganden av misstag:

Låt $\displaystyle f:D\to\mathbb{R}$, där $D$ är en öppen delmängd till $\mathbb{R}$. Välj ett kontinuerligt intervall $\displaystyle (a, b)\subseteq D$. Antag att det finns en areaberäknande funktion $A : [a, b] \to \mathbb{R}$, enligt $x\mapsto A(x)$, som beräknar arean mellan $a$ och $x$. För ett passande¹ $h>0$ ser vi att:

$\displaystyle hf\left(x\right)\le A\left(x+h\right)-A\left(x\right)\le hf(x+h)$

Detta medför att:

$\displaystyle \lim_{h \to 0} f\left(x\right)\le \lim_{h \to 0}\frac{A\left(x+h\right)-A\left(x\right)}{h}\le \lim_{h \to 0}f\left(x+h\right)$

Då $\displaystyle f$ är kontinuerlig på intervallet $[a, b]$ kommer $\displaystyle \lim_{h \to 0}f\left(x+h\right)=f\left(x\right)$

Vi ser således med hjälp av klämsatsen att:

$\displaystyle A'\left(x\right)=f\left(x\right)$

Eftersom vi har ett krav på $\displaystyle x$, nämligen att $x\in[a,b]$, måste vi bara hitta en primtiv funktion definierad på det öppna intervallet $(a,b)$. Kravet att $[a,b]$ ska vara ett kontinuerligt intervall gör att man slipper problem med hål. Således är:

$\displaystyle A\left(x\right)=F(x)+C$ en lösning till differentialekvationen ovan, där $\displaystyle F'\left(x\right)=f\left(x\right)$, för alla $x\in(a,b)$.

[1] När jag skriver att $h$ ska vara passande menar jag att man ska välja ett $h$, sådant att olikheterna ovan stämmer, och att "derivatan" av $A$ ska gå att beräkna.

Det som känns lite konstigt med det jag har slängt ihop här är att jag blandar öppna och stängda intervall. Problemet är följande: om intervallet inte är stängt, kommer man inte kunna få en "area" som är 0 (om ändpunkten är samma som startpunkten). Men om intervallet är stängt kommer man inte kunna derivera funktionen eftersom def.mängden måste vara öppen för att gränsvärden ska gå att beräkna. Detta blir problematiskt i den andra olikheten i "olikhetskedjan". Jag tror inte den derivatan går att beräkna utefter hur jag definierade min funktion $A$.

Och jag märker att tråden börja slira iväg från ursprungsfrågan. Jag grönmarkerar tråden efter den här frågan.

Nu har ni sprungit vidare ordentligt i tråden ser jag :-)

Jag tänkte kanske ge dig ett förslag på hur man kan definiera en yt (area)beräkningsfunktion och jag tänkte återigen påpeka det fina med att jobba med intervall istället för öppna mängder gällande konceptet "primitiv funktion", men innan dess undrar jag över din olikhet här

$hf(x)\leq hf(x+h)$ för $h>0$

Vilka krav ställer det på funktionen $f$? Hur löser vi det?

Att f är monotont växande på intervallet, måste nog vara ett krav. Eller åtmistone att f’(x)>=0.

Om f’< 0 så måste vi vända på olikhetstecknet

Ja, det är korrekt. Du har i princip visat att $F$ är en primitiv funktion till $f$, men bara under förutsättning att $f$ är växande (monoton), större än noll samt under några implicita antaganden om $A(x)$. Dessutom bör man säga något om huruvida $f(x)$ är begränsad och har ett största och ett minsta värde på intervallet.

Ändpunkterna i intervallet är inte något större problem. En (primitiv) funktion $F$ är deriverbar på ett öppet intervall $]a,b[$ om $F$ är deriverbar i varje punkt i $]a,b[$. Om dessutom $F^\prime_+(a)$ och $F_{-}^\prime(b)$ existerar, så är $F$ deriverbar på det slutna intervallet $[a,b]$ per definition.

Men vi vill gärna att funktionen $f$ ska kunna såväl växa som avta och dessutom ibland vara mindre än 0 (växla tecken). Dessutom vill vi kanske ha ett lite fastare grepp om areamåttet för ett göra beviset rigoröst.

Ett betydligt bredare antagande är låta $f$ vara kontinuerlig på ett intervall $[a,b]$. För att göra det enklare för oss antar vi också att $f(x)\geq 0$ för alla $x\in I$. Senare kan vi generalisera satsen till funktioner som får växla tecken med ett "standardtrick". Men först måste vi som sagt göra något åt areamåttet:

Om funktionen $f$ är kontinuerlig på det slutna begränsade intervallet $[a,b]$ och $f(x)\geq 0$ för alla $x$ i $[a,b]$, så är punktmängden

$G[a,b]=\{(x,y): a\leq x\leq b, 0\leq y \leq f(x)\}$

mätbar med måttet

$m(G)=\lim_{n\to \infty}\sum_{k=1}^n \frac{b-a}{n}f(a+\frac{k}{n}(b-a))$

Om du nu låter $c$ vara en fix punkt i funktionens intervall (skilj alltså på intervallen för areamåttet och funktionen) så kan den primitiva funktionen $F$ vara

Nu kan du använda en variant av det upplägg du tänkte från början men det blir lättare att särskilja de olika fallen. För högerderivatan av $F(t)$ med $t\geq c$ och $h>0$ samt $t+h\neq b$ studerar man alltså differenskvoten

$\frac{F(t+h)-F(t)}{h}$

Edit: Är det någon vet hur man får \cases att fungera på pluggakuten?

Du kan använda \array. Oggih har använt det en del, citera ett av hans inlägg så kan du se hur man formatterar det.

(tack för svaret, ska läsa igenom när jag kommer hem och försöka återkomma med en korrigerad formulering av satsen!! :))

EDIT: jag kan redigera inlägget åt dig med array-controlsequencen om du vill :)

Så, nu har jag äntligen möjlighet att skriva igen.

Jag har några frågor angående ditt inlägg som jag måste ställa och reda ut innan jag kan försöka formulera om satsen.

1. Använder vi en utvidgad variant av derivatans definition när vi säger att en funktion är deriverbar över ett stängt intervall? Vanligtivs talar vi ju om följande definition:

$\displaystyle F'\left(x\right)=\lim_{h \to 0} \frac{F\left(x+h\right)-F\left(x\right)}{h}$

Men ett "vanligt" gränsvärde kan ju inte existera i en ändpunkt i ett intervall. Menar du att då vi betraktar derivatan i $x=a$ så studerar vi egentligen gränsvärdet då $\displaystyle h\to0^{+}$? Och på motsvarande sätt gränsvärdet då $h\to 0^{-}$, då vi studerar punkten $x=b$?

2. Vad innebär det att en punktmängd är mätbar? Vad är ett mått? Jag känner på mig att dessa är ganska breda frågor, men jag har aldrig hört dessa begrepp innan. Det du har skrivit upp är ju en Riemannsumma, men jag förstår inte vad begreppet mått innebär här.

Och mitt erbjudande om att redigera ditt inlägg och fixa med \array-controlsequencen är fortfarande aktuellt :)

Tillägg: 1 jul 2024 14:05

EDIT: redigerade ett skrivfel i början av fråga 1.

Vi behöver inte bry oss om att ändra till arrayer. \cases sitter i mitt muskelminne och var bara nyfiken på om någon fått cases att funka :-)

Du tänker rätt kring derivatan och dess gränsvärden. Men vi introducerar ingen "utökad" definition av derivata utan använder den gängse definitionen av deriverbar funktion. Följandet gäller som allmän definition

Om $f$ är deriverbar i åtminstone en punkt av sin definitionsmängd ($D_f$), så är $x\mapsto f^\prime(x)$ en ny funktion.

$f^\prime: x \mapsto f^\prime(x), \text{där }D_{f^\prime}=\{f^\prime(x) \text{ existerar }\} \subseteq D_f$

Om dessutom $f$ är deriverbar i varje punkt av sin definitionsmängd, dvs om $D_f=D_{f ^\prime}$, säger man att $f$ är en deriverbar funktion. Allmänt gäller att $f$ är deriverbar på ett intervall $I\subset D_f$ om restriktionen $f_I$ av $f$ till $I$ är en deriverbar funktion. Om $f$ är deriverbar på ett öppet intervall $]a,b[$ och höger- respektive vänsterderivatan existerar säger man att $f$ är deriverbar på det slutna intervallet $[a,b]$. Med högerderivata menar man mycket riktigt att man närmar sig gränspunkten från höger och man brukar använda en annan men matematiskt sett identisk definition så här för högerderivatan ($h=x-x_0$):

$f^\prime(x_0)=\lim_{x\to x_0^+}\frac{f(x)-f(x_0)}{x-x_0}$

Några exempel:

Funktionen $\sqrt{x}$ har $D_f=[0,\infty[$, men saknar högerderivata i $0$ alltså är funktionen $\sqrt{x}$ inte deriverbar. Däremot är $\sqrt{x}$ deriverbar på intervallet $]0,\infty[$.

Funktionen $|x|$ har högerderivatan $1$ och vänsterderivatan $1$ på intervallet $[0,1]$ och är deriverbar i varje punkt i $]0,1[$. Alltså är $|x|$ deriverbar på $[0,1]$. Man kan på samma sätt visa att $|x|$ är deriverbar på $[-1,0]$. Däremot är $|x|$ inte deriverbar på $[-1,1]$.

Funktionen $1/x$ är deriverbar i varje punkt av sin definitionsmängd, $D_f=D_{f^\prime}$ och är därmed i motsats till våra två tidigare funktioner ett exempel på en deriverbar funktion.

Ett mått är ett sätt att mäta något. Till exempel hur många bokstäver det finns i ordet "mått". Det finns fyra bokstäver, dvs $\mu("\text{mått}")=4$. Vi vill gärna kunna mäta saker som en kurvas längd eller arean, dvs utbredningen, av en punktmängd i planet. Vi vill också ge måttet vissa egenskaper, till exempel att det är ett reellt tal $\geq 0$ och att addition av två områden ger det intuitivt förväntade resultatet $m(A\cup B)=m(A)+m(B)-m(A\cap B)$. Vidare borde arean av en ensam punkt $p$ (som saknar utbredning i rummet) vara $m(p)=0$. En union av av ändliga sträckor  är ett annat exempel på något som borde ge oss måttet 0 (ibland kallar man en mängd som ger måttet 0 för nollmängd).

För att mäta arean av en punktmängd $G$ kan man tänka sig att man först täcker över området med ett antal axelparallella rektanglar så att området helt täcks, vi kallar denna övertäckning $E$. Sedan tänker vi oss att vi bara täcker delar av området med rektanglar som ligger inom området och vi kallar denna deltäckning $e$. De gäller alltså att $e\subseteq G \subseteq E$

En begränsad punktmängd $G$ i planet är mätbar om det finns ett och endast ett tal $\alpha$ sådant att

$m(e)\leq \alpha\leq M(E)$

För varje deltäckning $e$ och varje övertäckning $E$ av $G$. $G$ tilldelas då areamåttet $m(G)=\alpha$. Senare visar det sig att denna till synes något godtyckliga definition på ett bekvämt vis uppfyller de flesta krav vi rimligtvis kan ställa på ett areamått.

Men vissa punktmängder är inte mätbara med våra nya definition. Det beror på att det finns mer än ett tal $\alpha$ som uppfyller villkoret. Ett exempel på en icke mätbar mängd är

$G=\{(x,y): 0\leq x \leq 1, 0 \leq y \leq 1, x\in Q, y\in Q\}$.

Eftersom varje rationell punkt omges av "hål" i det reella planet är $m(e)=0$ för varje möjlig deltäckning och $m(E)\geq 1$ för varje möjlig övertäckning.

Ämnet mått är ett (oerhört intressant och givande) kaninhål som bland annat berör hur man definierar integraler (till exempel Riemann vs Lebesgue). Men jag tänker att det åtminstone förtjänar en helt egen tråd :-)

Ah okej!

Så vår punktmängd $G$ är alltså endast ett sätt att beskriva arean på det aktuella området? Alltså skapar vi en mängd av alla punkter som innesluter området. Och sedan skapar vi ett mått, någon slags funktion, för att kunna mäta "storleken" på vår punktmängd, dvs. "utbredningen" i xy-planet? Och i vårt fall räckte det med att använda en Riemannsumma som mått, eftersom funktionen är kontinuerlig över det aktuella intervallet?

Tillägg: 1 jul 2024 16:39

Men jag är lite fundersam kring vad du menar med $E$ och med $e$. Kan $E$ täcka mer (eller mindre) än hela arean? Det kommer nog alltid bli så, såvida funktionen inte är rektangulär.

Och hur menar du att vi gör deltäckningar? Försöker vi då också täcka hela arean, fast med mindre rektanglar? Eller vill vi bara täcka bitar?

Tillägg: 1 jul 2024 16:55

(och jag ska skapa en ny tråd inom kort!)

EDIT: tog bort en hjärndöd del av mitt inlägg. Ingen aning vad jag tänkte.