Hur integrerar jag (1-x^2)^0.5
Hej!
Jag ska försöka integrera (1-x^2)^0.5.
Första tanken var att utnyttja roten ur regler, men olyckligtvis funkar inte det: Min andra ide var att:
Min andra ide var att:
 Men insåg efter att jag skulle försöka med partiell integration att f'(x) kommer att innehålla x, även om jag deriverar funktionen. Detta medföljer att i och med att jag behöver integrera igen efter minustecknet så kommer jag behöva använda samma sats igen, i vad jag förmodar all oändlighet.
Men insåg efter att jag skulle försöka med partiell integration att f'(x) kommer att innehålla x, även om jag deriverar funktionen. Detta medföljer att i och med att jag behöver integrera igen efter minustecknet så kommer jag behöva använda samma sats igen, i vad jag förmodar all oändlighet.
Min tredje idé var att söka på internet, där jag hittade denna äldre tråd från pluggakuten:
https://www.pluggakuten.se/trad/behover-hjalp-med-antiderivatan-av-f-x-sqrt-10-2x/ Denna hjälpte till viss del, och gav mig iden med variabelsubstitution, men efter att ha lekt lite med det blev det också fel...
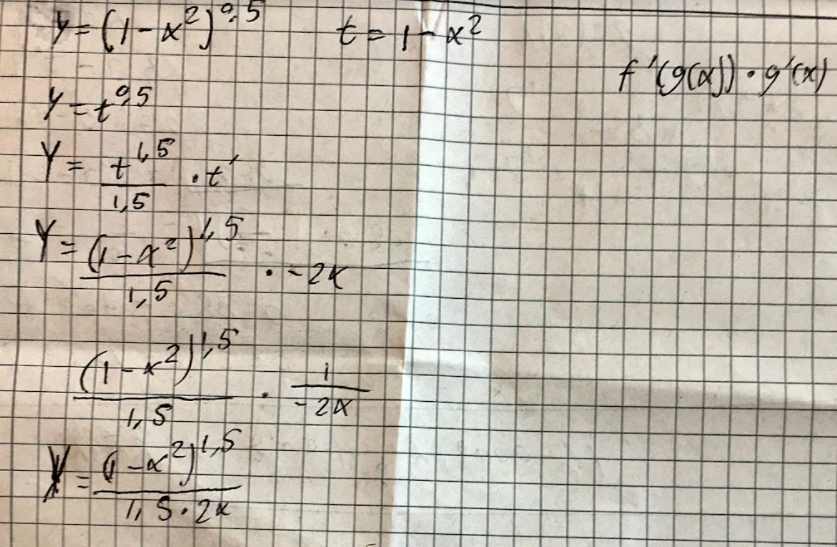
Detta påvisat genom att jämföra kurvan för integralen som geogebra fick (blå) och jämföra det med den jag fick (lila).

Tacksam för hjälpen!
Du kan prova en substitution t = sinx.
Laguna skrev:Du kan prova en substitution t = sinx.
Tacksam för hjälpen, men jag tror att jag gjorde något fel. Det överensstämmer tyvärr inte med geogebras lösning:

Förlåt, jag skrev fel. x = sint ska det vara.
Laguna skrev:Förlåt, jag skrev fel. x = sint ska det vara.
Det blir vidare problem när jag försöker integrera det, eller så kan jag bara inte se mönstret. Tänkte kanske att denna lagen kunde hjälpa mig:

Jag fastnade däremot:
Du glömmer bort dx
om x = sint så är dx = cos(t)dt
dessutom
1-sin^2(t) = cos^2(t)
Ett alternativ är att rita kurvan och fundera lite geometriskt.
Ture skrev:Du glömmer bort dx
om x = sint så är dx = cos(t)dt
dessutom
1-sin^2(t) = cos^2(t)
Menade du såhär?

Du måste ta med dx-dt substitutionen som jag skrev i förra inlägget.
Ture skrev:Du måste ta med dx-dt substitutionen som jag skrev i förra inlägget.
Jag är inte säker på vad du menar, vad skulle jag gjort annorlunda?
När du byter variabel från x till t så måste du ta med dx/dt av din substitution.
I ditt fall, x = sinx, ger att dx/dt = cost
I din integral har du en funktion f(x) och en term dx, när du byter funktion till g(t) måste du även byta dx till dt, i ditt exempel sk dx bytas mot cos(t) dt
Laguna skrev:Ett alternativ är att rita kurvan och fundera lite geometriskt.
 Tack för tipset! Jag testade den integralen som jag fick fram genom den tidigare uträkningen. Men jag är osäker på hur jag skulle kunna ändra sinuskurvan för att få den att vara lik den orangea linjen.
Tack för tipset! Jag testade den integralen som jag fick fram genom den tidigare uträkningen. Men jag är osäker på hur jag skulle kunna ändra sinuskurvan för att få den att vara lik den orangea linjen.
Jag menade att rita originalfunktionen, med x som variabel.
Ture skrev:När du byter variabel från x till t så måste du ta med dx/dt av din substitution.
I ditt fall, x = sinx, ger att dx/dt = cost
I din integral har du en funktion f(x) och en term dx, när du byter funktion till g(t) måste du även byta dx till dt, i ditt exempel sk dx bytas mot cos(t) dt
Jag tror att jag har fått det om bakfoten, eller så ser jag inte det hela. 
Laguna skrev:Jag menade att rita originalfunktionen, med x som variabel.
Menar du ?
Laguna skrev:Jag menade att rita originalfunktionen, med x som variabel.
Jag ser möjligheten till en likhet, men jag vet inte hur jag ska ta mig vidare härifrån?

Titta bara på originalkurvan. Ser det ut som en bekant form?
Laguna skrev:Titta bara på originalkurvan. Ser det ut som en bekant form?
Jag hittade att den var lik cirkelns ekvation, men jag kommer bara tillbaka till frågeställningen ovan:
Cirkel, ja. Om du markerar x = a med en linje, kan du räkna ut arean för den del av cirkeln som ligger mellan x=0 och x=a med geometriska/trigonometriska metoder?
Etthejfrånpolhem skrev:Ture skrev:När du byter variabel från x till t så måste du ta med dx/dt av din substitution.
I ditt fall, x = sinx, ger att dx/dt = cost
I din integral har du en funktion f(x) och en term dx, när du byter funktion till g(t) måste du även byta dx till dt, i ditt exempel sk dx bytas mot cos(t) dt
Jag tror att jag har fått det om bakfoten, eller så ser jag inte det hela.
Integralen ser väl ut så här:
Om du vill substituera
x = sin(t), derivera det med avseende på t vilket ger dx/dt = cos(t)
vilket medför att dx = cos(t) dt
Nu skriver vi in det i din integral
som vi kan förenkla till
vilket vi förenklar ytterligare
som återstår att lösa, antingen genom att titta i formelbladet eller också skriver vi om med halva vinkeln,
Ture skrev:Etthejfrånpolhem skrev:Ture skrev:När du byter variabel från x till t så måste du ta med dx/dt av din substitution.
I ditt fall, x = sinx, ger att dx/dt = cost
I din integral har du en funktion f(x) och en term dx, när du byter funktion till g(t) måste du även byta dx till dt, i ditt exempel sk dx bytas mot cos(t) dt
Jag tror att jag har fått det om bakfoten, eller så ser jag inte det hela.
Integralen ser väl ut så här:
Om du vill substituera
x = sin(t), derivera det med avseende på t vilket ger dx/dt = cos(t)
vilket medför att dx = cos(t) dt
Nu skriver vi in det i din integral
som vi kan förenkla till
vilket vi förenklar ytterligare
som återstår att lösa, antingen genom att titta i formelbladet eller också skriver vi om med halva vinkeln,
Tacksam för hjälpen!
Men det är fortfarande en saker jag inte förstår:
Hur kommer det sig att vid steget då man substiterar så blir det:
A:
och inte:
B:
(motiveringen bakom B ligger i att vi ska ju bara ersätta x med sin(t)).
Ture skrev:
Om du vill substituera
x = sin(t), derivera det med avseende på t vilket ger dx/dt = cos(t)
vilket medför att dx = cos(t) dt
Nu skriver vi in det i din integral
joculator skrev:Ture skrev:
Om du vill substituera
x = sin(t), derivera det med avseende på t vilket ger dx/dt = cos(t)
vilket medför att dx = cos(t) dt
Nu skriver vi in det i din integral
Detta kan stämma, men jag förstår inte varför det händer när jag integrerar. Jag menar det är inget jag brukar se när jag integrerar, men jag brukar använda det när jag deriverar:

kolla denna video https://www.youtube.com/watch?v=XbCRlnWnDwk
läs mer här
http://www.matteguiden.se/matte-f/integraler/variabelsubstitution/








