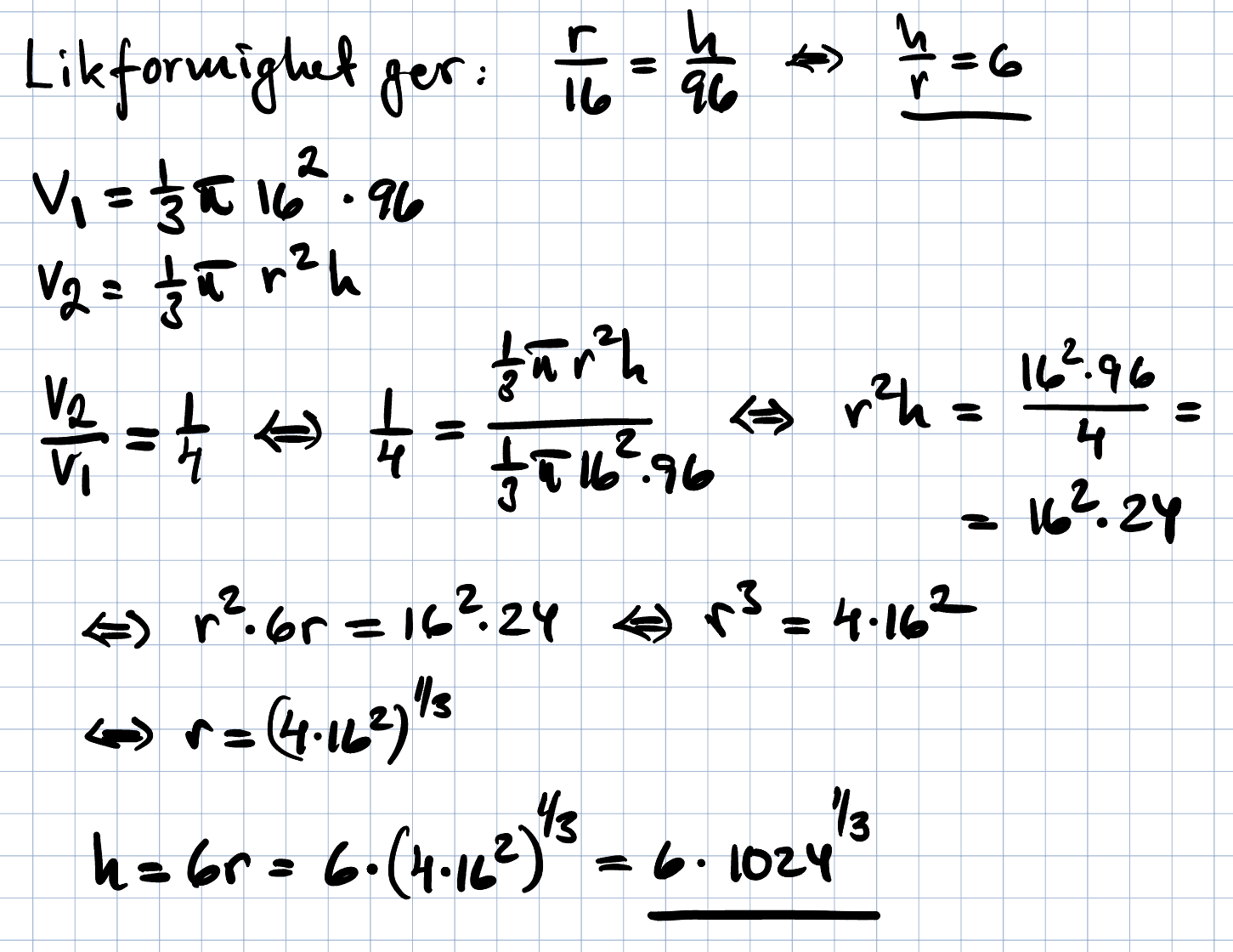Hur högt når vattnet
Uppgift 4511:

Lösning: Jag tänkte att vi skulle diskutera olika lösningar till denna uppgift. Dessa två lösningar ger rätt svar. Den första lösningen har jag hämtat från Internet medan den andra är facits lösning.
Jag tänkte att vi skulle diskutera olika lösningar till denna uppgift. Dessa två lösningar ger rätt svar. Den första lösningen har jag hämtat från Internet medan den andra är facits lösning.
Formeln för en kon (vilken är glasstrutens form), är (B*h) / 3 = . Nu kan man inte utan omvägar ta steget att 96 centimeter som glasstrutens höjd är kan delas på 4 och bli 24 cm. Det skulle motsvara 25 procent av hela glasstrutens höjd, men det är när glasstruten är fylld till 25 procent som vi vill ha reda på. Beräkningen blir därmed . Men hur kommer vi fram till svaret? Jag har mina gissningar, men ska väl inte elaborera allt för mycket utan skulle gärna vilja få veta mer från er här. Förklara gärna både min lösning som jag hämtade från Internet och facits lösning.
God helg allihopa!
Var är facits lösning?
Lösningarna utnyttjar ju samma principer. Man måste veta förhållandet mellan höjden och radien och sedan veta formeln för en kons volym. Bra uppgift tycker jag.
Smaragdalena skrev:Var är facits lösning?
Se min infogade bild där jag skrivit ut en uträkning. Har dragit en pil till Facits lösning.
Iridiumjon skrev:Lösningarna utnyttjar ju samma principer. Man måste veta förhållandet mellan höjden och radien och sedan veta formeln för en kons volym. Bra uppgift tycker jag.
Behöver man veta förhållandet mellan höjden och radien? Min första lösning, det vill säga , använder enbart likformigheten mellan höjden.
Man måste veta att förhållandet mellan höjden och radien är konstant, d v s att konerna är likformiga.
Smaragdalena skrev:Man måste veta att förhållandet mellan höjden och radien är konstant, d v s att konerna är likformiga.
Själva uppgiften kan lösas genom att om man minskar radien och höjden med ett tal så minskas volymen med det talet upphöjt till tre. Då radien multipliceras två gånger och höjden en gång, är det 2+1 = 3.
Man ska alltså dela höjden med det tal som då det upphöjs till tre blir fyra, dvs tredje roten ur fyra.
Jag parafraserar en annan person som löst denna uppgift på internet. Jag har svårt att förstå detta med beräkningar. Skulle du Smaragdalena, kunna hjälpa mig förstå detta genom räkneexempel?
Jag ska försöka beskriva hur jag löser denna uppgift. Med resonemang och beräkningar ska jag försöka åstadkomma en fullgod lösning.
Volymen för en kon: . Vi vill alltså ha höjden när denna kon är fylld till 25 % från dess spetsiga topp. Minskar jag nu volymen till 1/4, så vill jag veta hur lång konens höjd var när den har 1/4 av sin fulla kapacitet. Eftersom vi i beräkningen har radien upphöjt till 2 gånger höjden, så behöver vi dela höjden med tredje roten ur 4, då det är några steg innan konen har full kapacitet. För att få reda på den höjden ska vi ha . Förstår dock inte varför denna beräkning inte räknar från botten på konen till toppen, det vill säga från den runda sidan upp till den spetsiga toppen.
Änvände de här två inläggen för att lösa uppgiften:
https://www.pluggakuten.se/trad/likformighet-kon-1/
https://www.pluggakuten.se/trad/geometri-prov-fraga-fragor/
Här är min första lösning där jag utnyttjar formeln för en kons volym:

Min andra lösning utnyttjar jag sambandet

Kommentera gärna min uppgift och rätta sådant jag har betecknat fel eller givit fel beskrivning.
Hej! Hittade den här uppgiften i en gammal mattebok och löser den på två sätt:
1. Volymskalning: En faktor s = 0.25^(1/3) att skala höjden med
2. Ekvationslösning: (1/3)*x*(x/6)^2*pi = 25 % av totala volymen
Som tidigare nämnts säger facit 6*1024^(1/3) som ju är c:a 60,5, men hur kommer man fram till det exakta svaret 6*1024^(1/3)?
Hej och välkommen hit.
96 / 4^(1/3)
96 är 6*16 är 6 * 4096^(1/3)
96 * (4096/4)^(1/3)
danneenkelp skrev:Hej! Hittade den här uppgiften i en gammal mattebok och löser den på två sätt:
1. Volymskalning: En faktor s = 0.25^(1/3) att skala höjden med
2. Ekvationslösning: (1/3)*x*(x/6)^2*pi = 25 % av totala volymen
Som tidigare nämnts säger facit 6*1024^(1/3) som ju är c:a 60,5, men hur kommer man fram till det exakta svaret 6*1024^(1/3)?
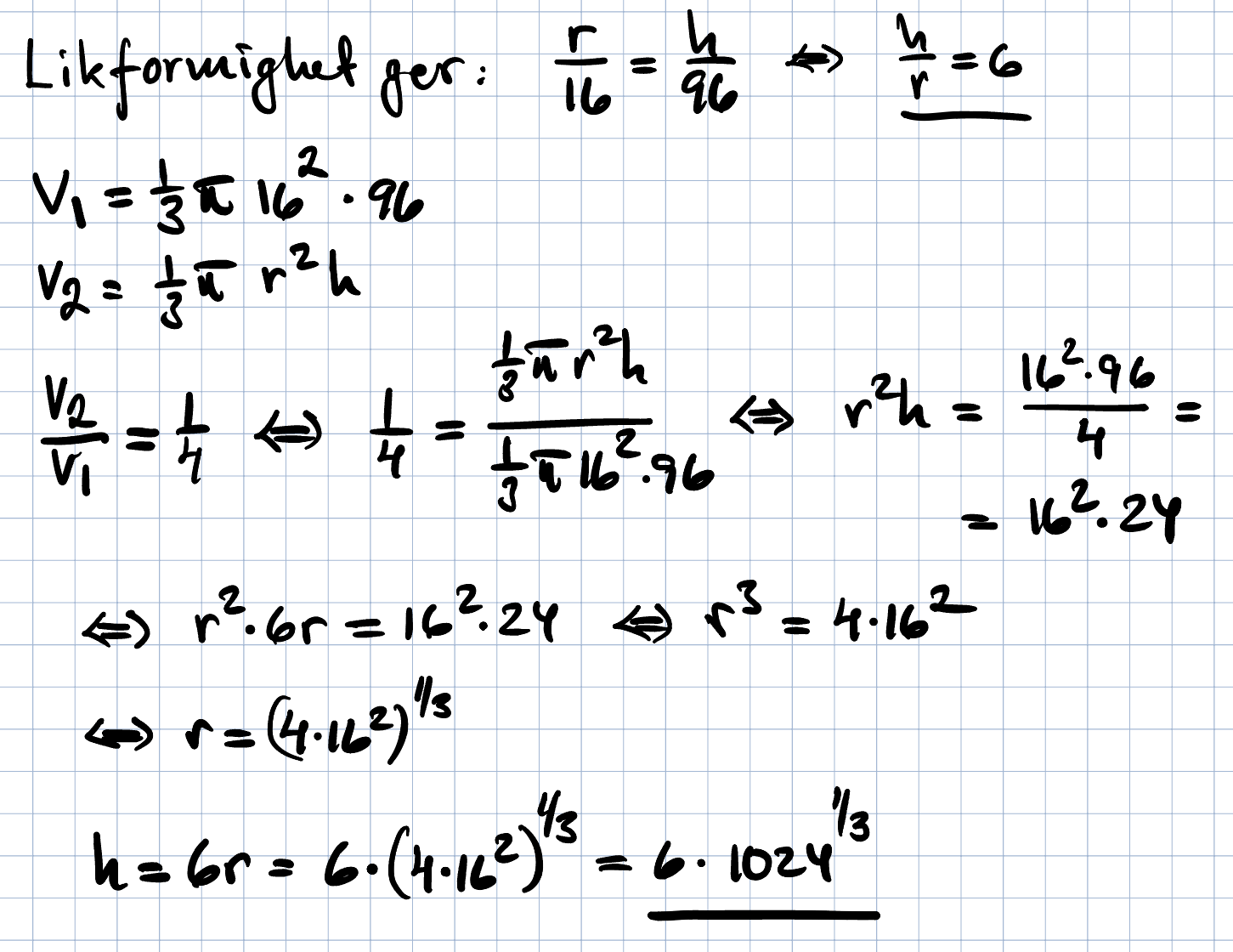
Bubo skrev:Hej och välkommen hit.
96 / 4^(1/3)
96 är 6*16 är 6 * 4096^(1/3)
96 * (4096/4)^(1/3)
Tack!
Hänger inte riktigt med på den här men det kanske ger sig om man låter det smälta lite. :)
Trinity2 skrev:danneenkelp skrev:Hej! Hittade den här uppgiften i en gammal mattebok och löser den på två sätt:
1. Volymskalning: En faktor s = 0.25^(1/3) att skala höjden med
2. Ekvationslösning: (1/3)*x*(x/6)^2*pi = 25 % av totala volymen
Som tidigare nämnts säger facit 6*1024^(1/3) som ju är c:a 60,5, men hur kommer man fram till det exakta svaret 6*1024^(1/3)?
Tack! Den var lätt att förstå :)