Hur genomfördes denna förenkling med i?
Hej allesammans!
Jag ville fråga er hur denna förenkling genomfördes? Det verkar som att de imaginära delarna tar ut varandra?
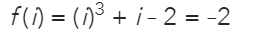
Min bästa gissning är att man skriver om till , då får man , och att man sen omvandlar det till och då får man slutligen bara -2 kvar.
MEN - när man räknar med komplexa tal så ska man väl räkna de imaginära och reella delarna var för sig och inte blanda dom? Dvs man får egentligen inte skriva om -1*i till -1i för då blandar man ihop -1:an och i:et...?
(har en stark känsla av att detta är en väldigt dum fråga alltså)
Hej,
Kan du skriva av uppgiften i sin helhet eller ta en bild på den?
Självfallet!
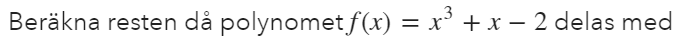

Facit:

Du får absolut göra som du gjort. När i höjs upp med två (eller någon annan jämn exponent) kan det slås in i den reella delen.
Mrpotatohead skrev:Du får absolut göra som du gjort. När i höjs upp med två (eller någon annan jämn exponent) kan det slås in i den reella delen.
Hmmm. Sant, jag slår in i^2 i den reella delen, så att den blir -1. Min fråga är egentligen om jag får blanda denna nyskapade reella del med den imaginära delen, dvs multiplicera -1 med i och få fram -1i? :)
-1 · i = -i
Varför hakar jag upp mig på detta egentligen... Det känns som att man då blandar reella och imaginära delar, vilket man inte får göra? (förutom när man omvandlar i^2 till -1)
ytrewq skrev:Varför hakar jag upp mig på detta egentligen... Det känns som att man då blandar reella och imaginära delar, vilket man inte får göra? (förutom när man omvandlar i^2 till -1)
Här blandar de ju inte några delar (läste lite noggrannare). -i är fortfarande imaginär, precis som 2i, 10i och 36/7i.
Tillägg: 1 maj 2024 21:14
Imaginär del och imaginärt tal är ju inte samma sak.
Ja precis, de delar jag känner blandas är när man tar -1 * i och får fram -1i. Då blandas en reell del (-1) med en imaginär del (i). Får man göra så?
Nu blandar du tal med del.
-1 är ett reellt tal som tillhör den imaginära delen. Det får multipliceras med ett annat imaginärt tal.
Kolla mitt tillägg till inlägg #8.
(Som Mesopotamia nu skrev)
Okay...! Kan man säga såhär: ett tal som tillhör den imaginära delen från början (tex i^2), den lämnar aldrig den imaginära delen/sfären trots att man omvandlar den till -1 istället? Betyder detta i så fall att -1:an inte får blandas med några reella delar, tex som -2 i mitt exempel?
(visste inte att imaginär del och imaginärt tal var olika saker heller, förresten! Bra att få lära sig det)
ytrewq skrev:Okay...! Kan man säga såhär: ett tal som tillhör den imaginära delen från början (tex i^2), den lämnar aldrig den imaginära delen/sfären trots att man omvandlar den till -1 istället? Betyder detta i så fall att -1:an inte får blandas med några reella delar, tex som -2 i mitt exempel?
Hmm, kollade upp det nu. Hade tydligen fel, typ, detta gäller:
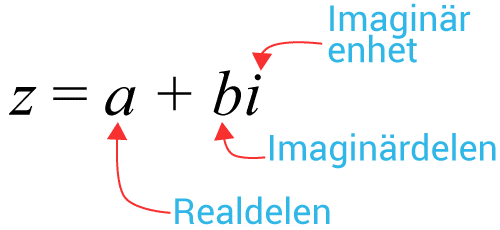
Den imaginära delen är således alltid ett reellt tal. Det talet du har i uppgiften har förresten ingen imaginärdel eller realdel förrän sista steget då den blivit -2. Först då har man "förenklat" den fullt och den står korrekt på formen a+bi (a=-2 och b=0). Tror det var detta som förvirra dig.
Ahhh! Ja, det var det som förvirrade mig! Så det fanns egentligen ingen "riktig" imaginärdel någonsin i uttrycket (eller den delen var lika med noll). Förstår då varför det verkligen var fritt fram att blanda runt grejer. Och bra påminnelse för mig att imaginärdelen även kan ha reella tal, att det blir en -1:a som multipliceras med tex i är inte alltför konstigt oavsett då ju.
Tack för hjälpen och tålamodet!


