Hur får jag in 0<t<125?
Hej, hur ska jag få in 0<t<125 i min differentialekvation.
Den jag har just nu ser ut på följande vis y'(x)=10-6y/250, y(0)=0
Uppgiften: en vattentank innehåller 250 liter rent vatten. En saltlösning med 2,.5g/l tillsätts med en hastighet av 4l/min. Saltlösningen blandar sig bra med vattnet. I botten av tanken tappas det ut 6l/min. Ställ upp och lös en differentialekvation som beskriver hur saltmängden y g i tanken ändrar sig med tiden t minuter då 0<t<125
Jag förstår ej frågan. (0,125) är definitionsintervallet och påverkar ej dina beräkningar.
Jaha. Drog bara en slutsats eftersom i andra exakt likadana uppgifter utan intervallet är svaret alltid för den urtappade saltmängden mängden 6y/250.
I facit står det att den urtappade saltmängden mängden är 6y/(250-2t). Varför?
Det där ser ej rätt ut, det skulle betyda
y=6y/(250-2t)
vilket är generellt fel.
Nej men hela differentialekvationen är y'(x)=10-6y/(250-2t). Förstår bara inte vart -2t kommer ifrån.
Jo, detta är ett litet annorlunda blandningsproblem.
Du har i din ekv. i stort rätt för dig, men tänk på at utflödet är STÖRRE än inflödet så tanken kommer att tömmas med tiden.
Nettot är 4-6=-2 liter/min och det innebär att volymen vatten är 250-2t, inte konstant 250 liter.
Så här ser det ut i MMA
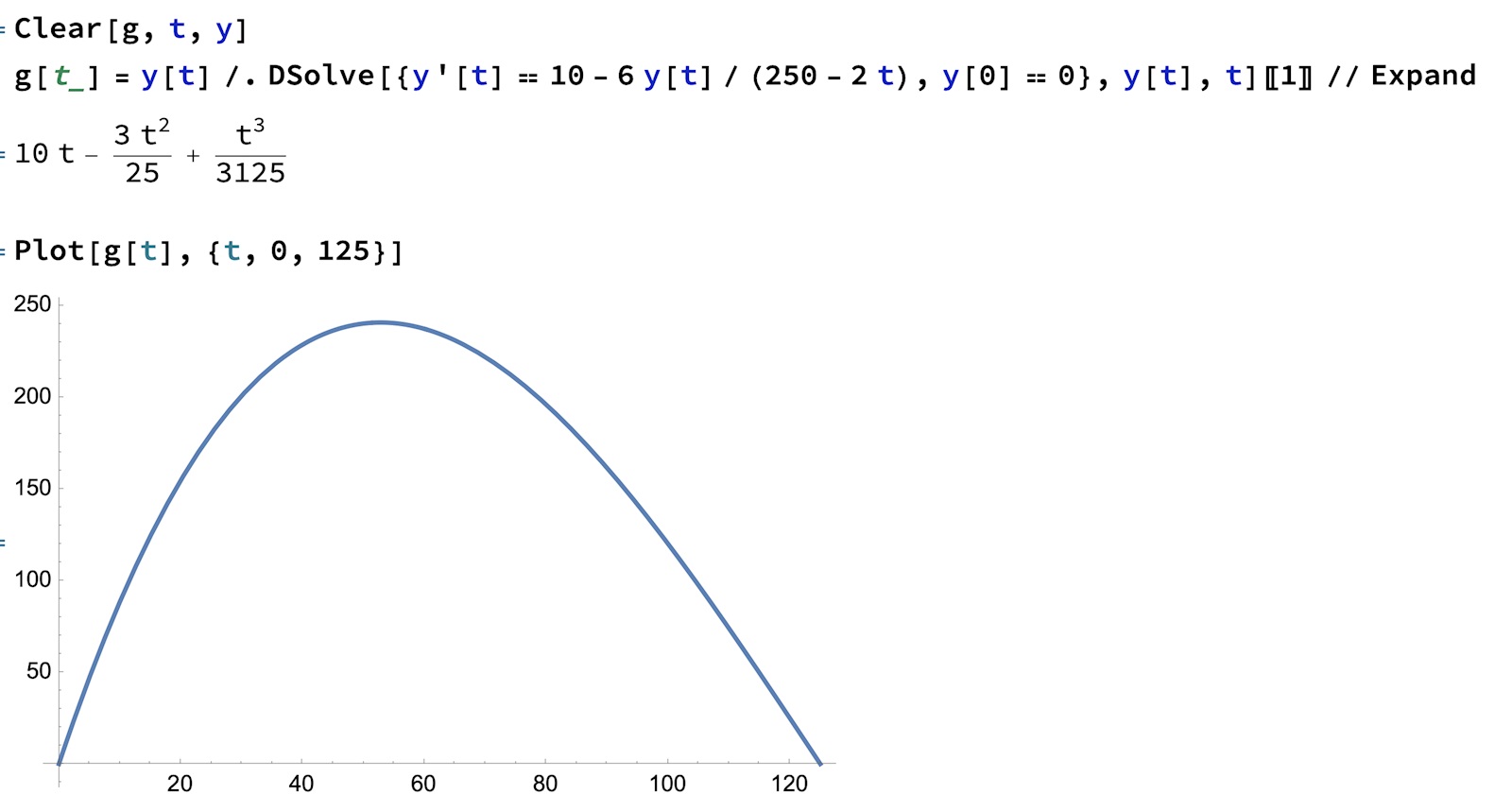
Så om inflödet och utflödet skulle varit lika mycket skulle jag inte behövt ha -2t i nämnaren?
Om inflödet var större än utflödet blir det då 6-4=2?
Hejsan266 skrev:Så om inflödet och utflödet skulle varit lika mycket skulle jag inte behövt ha -2t i nämnaren?
Om inflödet var större än utflödet blir det då 6-4=2?
Helt rätt tänkt,
a) då hade volymen varit konstant och blandningen planat ut
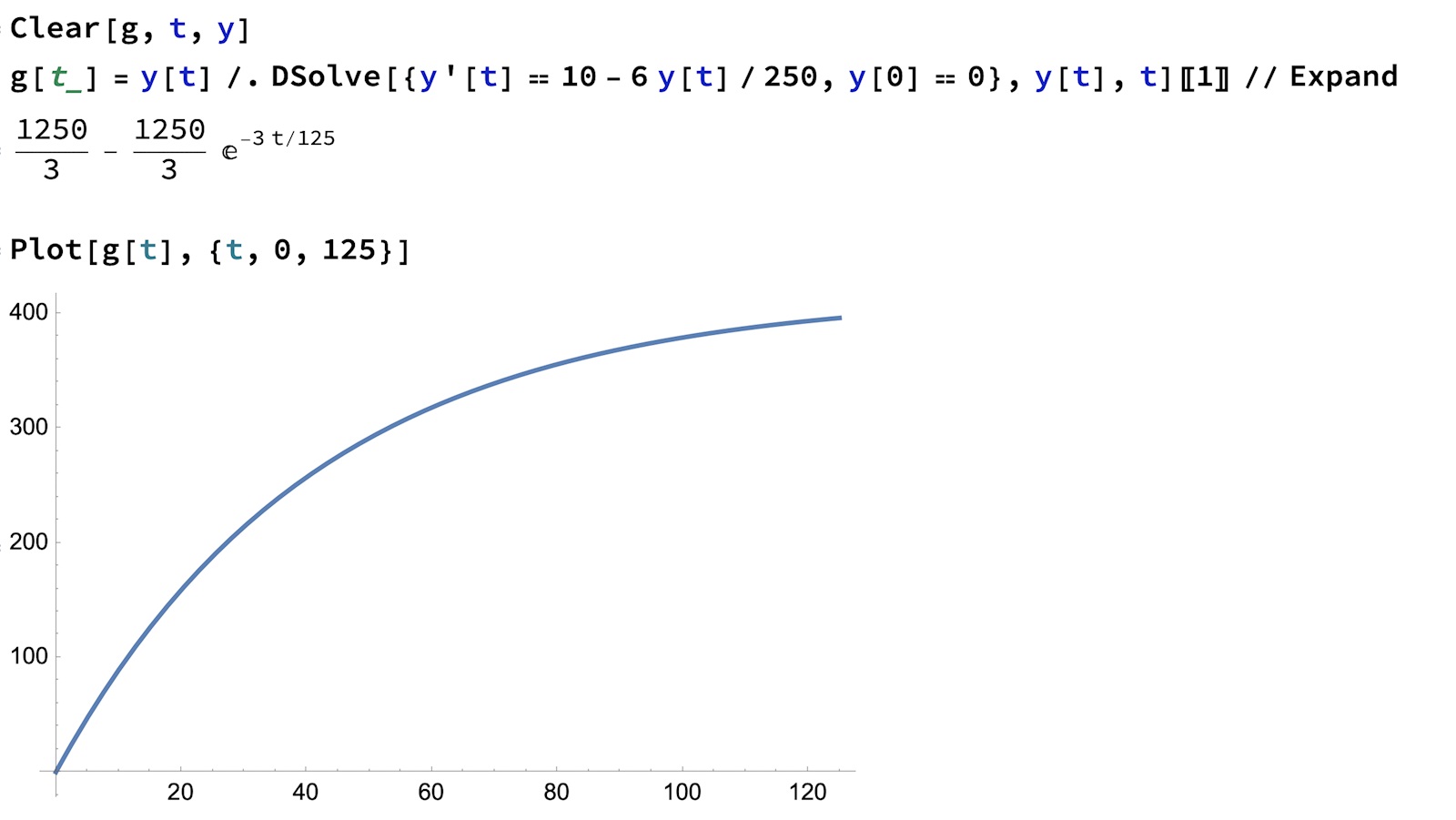
b) Helt rätt tänkt (igen). Här skenar allt iväg eftersom volymen ökar => saltmängden ökar
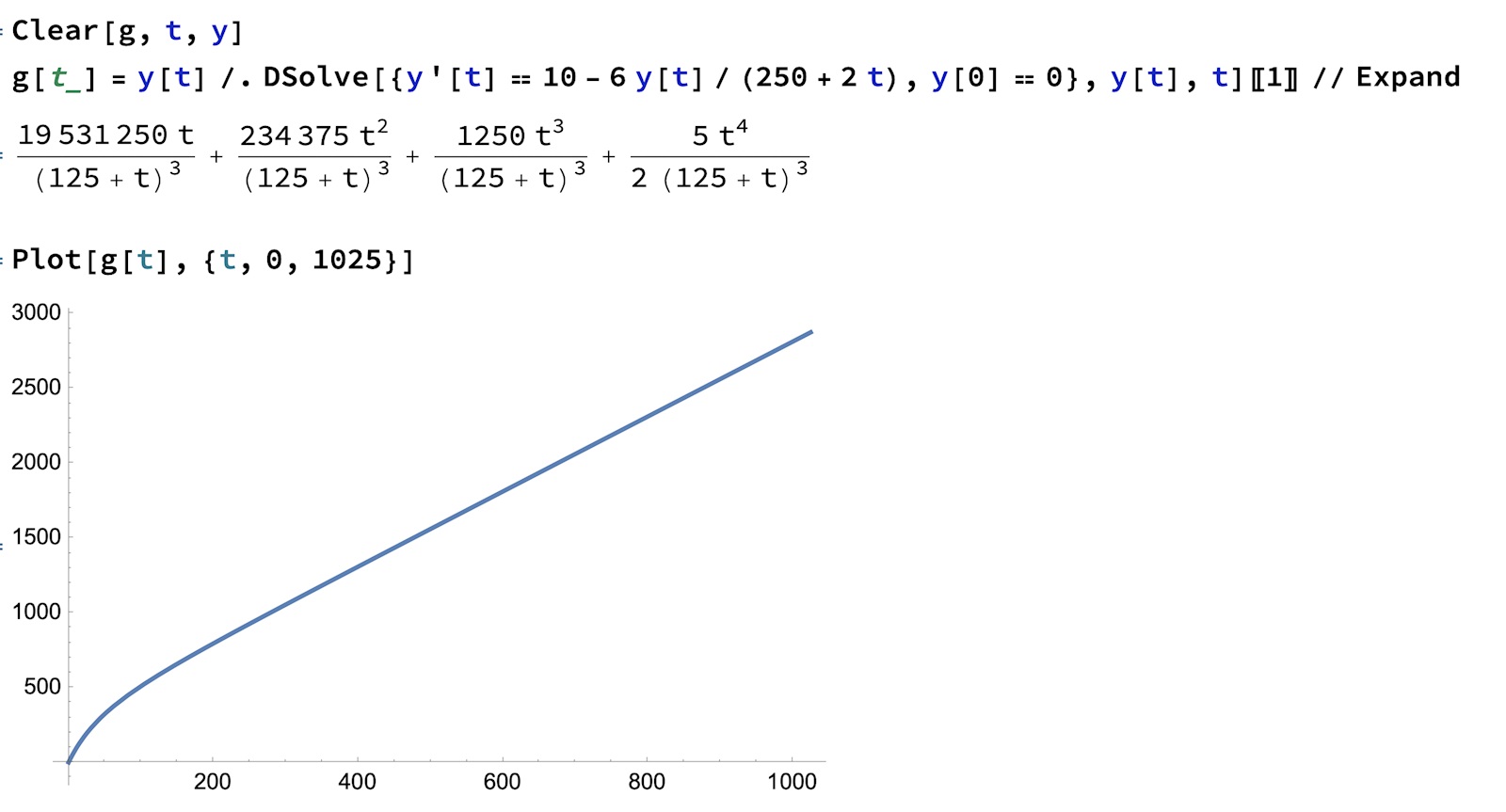
Några rätt iallafall. Var kommer intervallet in? Den verkar ju varken ha betydelse för min differentialekvation eller lösningen till den.
Hejsan266 skrev:Några rätt iallafall. Var kommer intervallet in? Den verkar ju varken ha betydelse för min differentialekvation eller lösningen till den.
Iom nettot är -2 L/min och vattenvolymen vid start är 250 L tar det 250/2=125 min innan tanken är tömd. Därefter rinner inflödet rakt ut och saltmängden *I* tanken = 0. Det är därmed meningslöst att fortsätta efter t=125. Jag anser dock att 0≤t≤125 är ett lämpligare intervall.
PS. Du löser den med integrerande faktor.

