Hur bryter dom ner det logiskt
Uppgiften är: 2120 faktorisera så långt som möjligt
Jag visar på uppgift 2119 c) hur jag tänker när jag gör såna här uppgifter. På c) så bryter jag ner det & kan se att jag får 2 st x/5 och 2st 2y/3 så jag kan därför se att jag ska placera ut de i varsin parentes.
men på uppgift 2120 så förstår jag inte riktigt hur jag ska bryta ner de för att få ett svar som visar mig att det ska bli 4(4+x)(4-x)
X:en tillhör ju 4x^2. & 64 har ju bara 1 4:A. Jag tänker alltså att 4x^2 = 2 * 2 * x * x är rätt enkel att se för då kan varje parentes få 1st 2x. Men 64 kan jag ju kanske skriva 4* 4*4 & får då 64 & då kan jag ju placera ut 1 st 4 i en parentes & en annan i den andra. Men då har jag ju 4 kvar.. ? Men om jag ska kontrollera de så blir de fel?
Du ser att 4 är en faktor, så börja med att bryta ut den: 64-4x2 = 4(16-x2).
Nu kan du använda konjugatregeln på 16-x2.
TACK lyckades lösa 2120 a, b & c men en fråga om det är ok. Vad gör man om de inte går att lösa ut någon? Exempelvis på d) så är det:
9y^2+24y+16
jag tänker:
9y^2 = 3 * 3 * y * y
24y = 3*8 * y
16 = 4* 4
här går de inte att hitta något gemensamt att bryta ut. Så jag tänker att det ska passa in i (a+b)^2 = a^2 + 2ab+ b^2 och 3y^2 går, och 4^2 går men de där 3*8*y blir ju något annat, så tänker att jag tänker fel här? : /
Man kan försöka få y2 att stå ensam. 9 är inte en faktor i de andra koefficienterna, men man får väl skriva bråk i så fall: 9(y2 + 24/9 y + 16/9) = 9(y2 + 8/3 y + 16/9).
Det var egentligen samma tanke med att bryta ut 4 förut: man får nånting där den högsta potensen har koefficienten 1 och därmed har störst chans att likna en känd formel.
Tack för svaret. okej, men förstår inte riktigt, för jag kolla facit och facit vill ha d) (3y + 4)^2. jag kanske skrev fel på uppgiften förr:
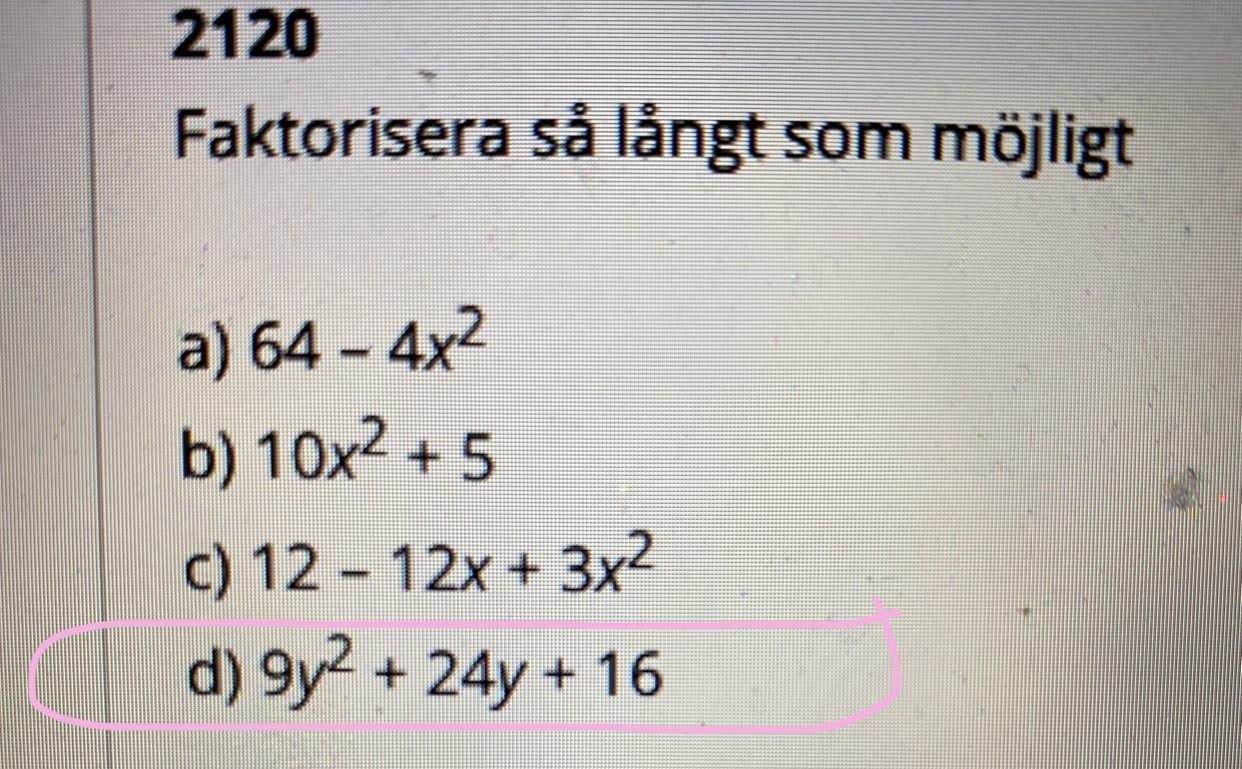
Kan du skriva y2 + 8/3 y + 16/9 som en kvadrat?
jag blir osäker, så vet inte. Det här är uppgifter i kap algebra, så kanske kommer jag in på mer sånt på kap 3
..
men jag gjorde/tänkte så här:
eftersom att 9y^2+24y+16 är typ (a+b)^2=a^2+2ab+b^2 så lät jag de vägleda mig lite. Tänkte typ att 9y^2+24y+16 ska på något vis passa mallen: (a+b)^2=a^2+2ab+b^2, så fick ut de så : ) tack
