Hej! Har du försökt något själv? Kan du exemplevis räkna ut sidorna BD och BC eftersom du vet att hypotenusen CD är 6 cm?
Ja låt mig skicka 1 sec
Snyggt, du har räknat ut alla sidor och omkretsen rätt! Okej, arean får vi genom att räkna ut var triangels area för sig.
Kan du räkna ut arean på den rätvinkliga triangeln, BCD? Basen gånger höjden delat med två.
Det rätta svaret är 16.8(abcd), men jag vet inte hur jag kommer fram till det. B*h/2?
Precis, formeln för att räkna ut arean av en triangel är:
Om du börjar med triangeln BCD så har den basen x och höjden x. Vad blir då arean? Du har redan räknat ut x.
4.24*4.24/2 = 9
Yes, perfekt. Då ska vi räkna ut arean av den andra triangeln, ABD. Du vet att basen är x, men du måste räkna ut höjden. Så här:
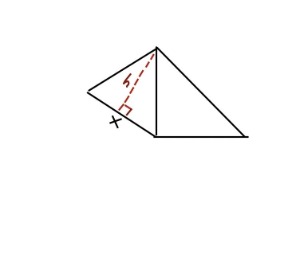
Du kan göra detta genom pythagoras sats, ser du hur?
Jag lite osäker men. 4.24^2+4.24^4=h
Inte riktigt. De två kateterna är h och en halv x. Hypotenusan är x. Ser du varför det blir så eller ska jag rita upp det?
Ja, snälla
h^2 = 4.24^2 - (0.5 * 4.24)^2 h^2 = 17.9776 - (0.5 * 4.24)^2 h^2 = 17.9776 - 2.12^2 h^2 = 17.9776 - 4.4944 h^2 = 13.4832 h ≈ √13.4832 h ≈ 3.67
är de rätt?'
Exakt så! Förstår du varför du skulle göra så? Här är bilden:
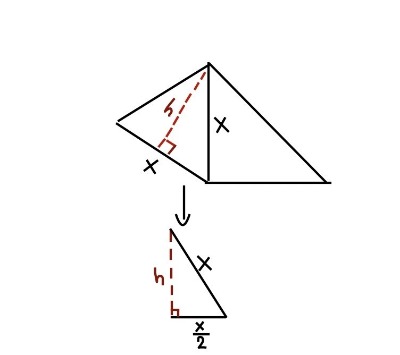
Okej, nu har du både höjden h och basen x för triangeln ABD. Nu kan du alltså räkna ut arean för triangeln ABD.
4.24^2-2.12^2=h^2 tack
Yes, bra. När du har arean av triangeln ABD kan du helt enkelt lägga ihop den med aren du räknade fram för triangeln BCD. Där har du svaret på figurens area :)
yes 7.8+9=16.8cm^2
Superbra :) Lycka till farmöver!
Ett annat sätt att beräkna arean av ABD är att använda areasatsen. Detta eftersom både sidlängder och vinklar är kända.
Sant. Den går man dock igenom först i matte 3.
Judit skrev:Sant. Den går man dock igenom först i matte 3.
Aha, OK. Jag har inte full koll på läroplanen.





