Hur bär jag mig åt för att beräkna avståndet mellan två koordinater?
"Hur långt är avståndet mellan punkterna (-1, 12) och (17, 50). Avrunda till två decimaler."
Med avstånd, menar man att ett steg i högerled är en längdenhet? Och hur bär man sig åt för att räkna ut detta? Jag känner att jag har rätt så bra koll på nästan allt som har med koordinatsystem att göra, men i detta fall kan jag helt ärligt inte komma på något sätt att lösa uppgiften...
Rita en ungefärlig skiss över koordinatsystemet med de två punkterna markerade. Posta bilden så hjälper jag dig vidare sedan.
Rita! Du kan använda Pythagoras sats.
Avståndet är roten ur(skillnad i x-led^2+skillnad i y-led^2)
PerEri skrev:Rita en ungefärlig skiss över koordinatsystemet med de två punkterna markerade. Posta bilden så hjälper jag dig vidare sedan.
https://gyazo.com/627ff32aca6fdfcb9baec68c858fa73c
La in bikden åt dig /Smaragdalena, moderator
Teraeagle skrev:Rita! Du kan använda Pythagoras sats.
Avståndet är roten ur(skillnad i x-led^2+skillnad i y-led^2)
Gäller inte Pythagoras sats trianglar?
Snygg figur, Vemood!
Om du ritar in ett linje från punkten (-1,12) rakt åt höger (dvs parallellt med x-axeln), och en linje från punkten (17,50) rakt nedåt (dvs parallellt med y-axeln) så skär dessa linjer varandra i punkten (17,12). Nu har du en triangel som du kan använda Pythagoras sats på. Rita, posta!
Det som du skrev Teraeagle, ska jag göra på detta viset?
-1 - 17 = 18 alltså delta x = 18
12 - 50 = -38 alltså delta y = -38
182 = 324
-382 = 1444
324 + 1444 = 1768
Roten ur 1768 = 42,04759208 är ungefär lika med 42,05
Korrekt?
https://www.matteboken.se/lektioner/matte-2/geometri/avstandsformeln
Se matteboken.se hur de skapar en triangel och därför kan använda Pythagoras sats.
Ser bra ut.
PerEri skrev:Snygg figur, Vemood!
Om du ritar in ett linje från punkten (-1,12) rakt åt höger (dvs parallellt med x-axeln), och en linje från punkten (17,50) rakt nedåt (dvs parallellt med y-axeln) så skär dessa linjer varandra i punkten (17,12). Nu har du en triangel som du kan använda Pythagoras sats på. Rita, posta!
https://gyazo.com/295b1bc2a21a8519a7171d9cbe0b8e7e
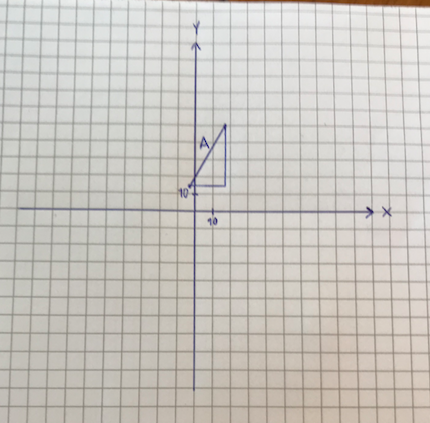La in bilden åt dig /Smaragdalena, moderator
Nu har jag gjort en triangel. Jag markerade sidan vars längd som ska beräknas med "A". Nu ska jag alltså använda Pythagoras sats? Då får jag läsa på om hur man gör detta..
Du får A i teckning. Mycket prydligt.
Triangeln du har ritat är rätvinklig. Hypotenusan är den sträcka du ska räkna ut (A i din figur), kateterna är dels sidan parallell med x-axeln, dels sidan parallell med y-axeln. Beräkningen du redovisade tidigare är rätt. Jag hoppas att du med figurens hjälp kan se varför man kan använda Pythagoras sats för att beräkna avståndet mellan två punkter i ett koordinatsystem.
Säg till om du vill diskutera det här mer.
Nu har jag hållt på och experimenterat ett tag samt läst på lite om Pythagoras sats. Vi har koordinaterna till alla hörn i triangeln, (-1, 12), (17, 50) och (17, 12) (den sista fick jag räkna ut de då två första var angivna i uppgiften). Det är ju linjen mellan (-1, 12) och (17, 50) som ska beräknas, är det då nödvändigt att använda Pythagoras sats då vi inte vet längderna på linjerna (-1, 12) och (17, 12) samt (17, 12) och (17, 50)?
Det som Teraeagle skrev förutsätter ju inte någon annan information än de koordinaterna som är angivna i uppgiften, dvs (-1, 12) och (17, 50). Med dessa kan vi addera (delta x)^2 + (delta y)^2 och göra en rotutdragning på summan.
-1 - 17 = -18 (delta x)
12 - 50 = -38 (delta y)
182 = 324
-382 = 1444
324 + 1444 = 1768
Roten ur 1768 = 42,04759208
Jag avrundar detta till 42,05 då uppgiften uppmanade till att svaret skulle anges i högst två decimaler.
Detta kan man ju åstadkomma utan att behöva rita en triangel, men min fråga är om detta stämmer?
Och tack så hjärtligt för all hjälp, det uppskattas oerhört mycket <3
Det stämmer alldeles utmärkt, och den beräkningen du gör är Pythagoras sats (delta-x är längden på sidan i triangeln som är parallell med x-axeln, och delta-y är längden på sidan i triangeln parallell med y-axeln).
Du skriver att du inte vet längderna på linjen mellan (-1,12) och (17,12), men det gör du. Den linjen är ett rakt streck parallell med x-axeln från x=-1 till x=17, dvs med en längd av 18 enheter. På samma sätt för den andra linjen. Kolla i min skiss (tyvärr inte lika snygg som din).
PerEri skrev:Det stämmer alldeles utmärkt, och den beräkningen du gör är Pythagoras sats (delta-x är längden på sidan i triangeln som är parallell med x-axeln, och delta-y är längden på sidan i triangeln parallell med y-axeln).
Du skriver att du inte vet längderna på linjen mellan (-1,12) och (17,12), men det gör du. Den linjen är ett rakt streck parallell med x-axeln från x=-1 till x=17, dvs med en längd av 18 enheter. På samma sätt för den andra linjen. Kolla i min skiss (tyvärr inte lika snygg som din).
JAHAAA! Okej nu trillade polletten ned, tack min vän.
