Högskoleprovet VT-18: lösningar

XYZ: Vilket svarsalternativ motsvarar $\frac{12a^2{b}^3}{4b^{2}c}$?

A: $\frac{12a^2}{4c}$

B: $\frac{3a^2}{bc}$

C: $3a^{2}c$

D: $\frac{3a^{2}b}{c}$

Om samma faktor förekommer både ovan och under ett bråkstreck kan de förenklas bort. Det medför att ett b blir kvar i täljaren, a:na och c:et är orörda, och $\frac{12}{4}=3$. Kvar blir då $\frac{3a^{2}b}{c}$. Svar: D

XYZ: Vilket svarsalternativ är korrekt?

A: $\frac{1}{2}<\frac{2}{5}<\frac{3}{4}$

B: $\frac{2}{5}<\frac{1}{2}<\frac{{\displaystyle 3}}{4}$

C: $\frac{3}{4}<\frac{5}{6}<\frac{7}{11}$

D: $\frac{3}{5}<\frac{1}{2}<\frac{3}{4}$

Börja med A, där vi direkt kan se att en halv är större än två femtedelar. Då går A bort. För B stämmer det att två femtedelar är mindre än en halv, som i sin tur är mindre än tre fjärdedelar. B är korrekt. Svar: B

XYZ:

$$\begin{gathered} f\left(x\right)=x^2 \\ g\left(x\right)=x^2·f\left(x\right) \\ h\left(x\right)=x^2·g\left(x\right) \end{gathered}$$

Vilket svarsalternativ motsvarar h(x)?

A: $x^2$

B: $3x^2$

C: $x^6$

D: $x^8$

Här krävs kunskaper om potensreglerna. 

$h\left(x\right)=x^2·g\left(x\right)=x^2·x^2·f\left(x\right)=x^2·x^2·x^2=x^6$

Svar: C

XYZ: Vilket av svarsalternativen är närmast $\mathrm{\pi }$?

A: $\frac{28}{7}$

B: $3$

C: $\frac{28}{8}$

D: $\frac{22}{7}$

Eftersom pi oftast skrivs avrundat i decimalform, är det smart att omvandla bråken till decimalform. 28 dividerat med sju är fyra, tjugoåtta dividerat med åtta är 3,5. För den som är van vid att använda tum kanske 22 genom sju låter bekant, eftersom detta bråk ofta används för att approximera pi. 22 genom sju kan snabbt räknas ut till att vara 3,1...(någonting), och är närmast pi. Svar: D.

XYZ:

Vad är $\frac{x}{5}-\frac{x}{3}-\frac{x}{2}$?

A: 0

B: - x

C: $\frac{x+5}{x}$

D: $-\frac{19x}{30}$

Den minsta gemensamma nämnaren är trettio. Förlängning till MGN ger $\frac{6x}{30}-\frac{10x}{30}-\frac{15x}{30}=\frac{{\displaystyle -19x}}{30}$. 

Svar: D.

XYZ: Vilken av linjerna går genom punkten (1, 3)?

A: $y=-x+4$

B: $y=-5x+2$

C: $y=3x+1$

D: $y=x-2$

Pröva! Sätt in att x = 1 och y = 3 i de olika ekvationerna. Då fås att A stämmer:

$$\begin{gathered} 3=-1+4 \\ 3=3 \end{gathered}$$, och det är onödigt att prova vidare.

XYZ: På en fotbollsmatch finns det exakt fyra gånger så många supportrar för hemmalaget som för bortalaget. Ingen person är supporter av båda lagen. Vilket svarsalternativ kan motsvara antalet supportrar på matchen?

A: 203

B: 214

C: 245

D: 262

Supportrarna förhåller sig som 4:1. Eftersom det inte kan finnas en halv supporter måste vi räkna med hela supportrar, och de måste gå att dela upp i fem grupper, då 4 + 1 = 5. Tal delbara med fem slutar på noll eller fem, och det enda alternativet som uppfyller detta kriterium är C, 245. 

Svar: C

XYZ: Vilket värde har x?

Sträckan c kan sägas vara hypotenusan i triangeln med kateterna 1 och x, vilket är en katet i den övre triangeln. Pythagoras sats ger att $c^2=2^2-1^2$, dvs. att $c=\sqrt{3}$. För att få ut längden av x upprepas processen en gång till: 

${\sqrt{3}}^2-1^2=x^2$

$x^2=2$

$x=\sqrt{2}$

(Den negativa roten förkastas eftersom sträckor inte kan vara negativa)

Svar: A.

XYZ:

$\frac{9x-13}{2}=1$

Vad är x?

A: $\frac{11}{9}$

B: $\frac{14}{9}$

C: $\frac{5}{3}$

D: $\frac{14}{3}$

Multiplicera båda led med två för att bli av med nämnaren i vänsterled. Använd sedan vanlig ekvationslösning:

$\frac{9x-13}{2}=1$

$9x-13=2$

$9x=15$

$x=\frac{15}{9}=\frac{5}{3}$

XYZ: Medianen av 77 på varandra följande heltal är 35. Vad är medelvärdet?

A: 35

B: 36

C: 37

D: 38,5

Två begrepp:

• Medianen av ett udda antal värden är det mittersta värdet.
• "På varandra följande heltal" är serier som 3, 4, 5, eller 18, 19, 20.

I detta fall har vi ett udda antal värden, vilket innebär att det mittersta värdet är medianen. Något som är intressant är att medelvärdet för ett udda antal på varandra följande heltal är det mittersta värdet. Alltså är medelvärdet 35, och svaret är A.

För den som är nyfiken på varför detta stämmer:

Kalla det mittersta värdet a, då är nästa tal $a+1$, och talet innan var $a-1$. Så fortsätter det ända ut tills kanterna nås. De yttersta värdena kommer att ha värdena (a - r) respektive (a + r). Eftersom r:en är lika stora men med motsatta tecken tar de ut varandra. Detsamma gäller för de näst yttersta talen, och de näst näst yttersta, osv. Sammantaget fås en rad med a:n, och medelvärdet av dessa är såklart a. 

XYZ: De två parallellogrammen är likformiga. 

$a<b$ och $c<d$

Att sidorna är likformiga innebär att sidan a förhåller sig till sidan c, som b förhåller sig till d. Alltså:

$\frac{a}{c}=\frac{b}{d}$. Lös sedan ut a genom att multiplicera båda led med c:

$\frac{a}{c}·c=\frac{b}{d}·c$

$a=\frac{bc}{d}$

Svaret är därför A. 

XYZ: a, b och c är tre på varandra följande heltal sådana att $\mathit{a}\mathbf{<}\mathit{b}\mathbf{<}\mathit{c}$. Vilket svarsalternativ är $\mathbf{3}{\mathit{a}}^{\mathbf{2}}\mathbf{+}{\mathit{c}}^{\mathbf{2}}$ med säkerhet jämnt delbart med?

A: 3

B: 4

C: 5

D: 6

Att de är på varandra följande innebär att c kan skrivas som $a+2$. c upphöjt i två kan då skrivas som ${\left(a+2\right)}^2$. Totalt ger det:

$$\begin{gathered} 3a^2+(a+2{)}^2= \\ 3a^2+a^2+4a+4= \\ 4a^2+4a+4 \end{gathered}$$

Bryt ut en fyra:

$4(a^2+a+1)$

Eftersom faktorn fyra garanterat ingår i uttrycket är talet garanterat delbart med fyra. 

Svar: B, 4.

KVA:

Kvantitet I: ${\left(\frac{7}{9}\right)}^2$

Kvantitet II: $\frac{50}{80}$

A: Kvantitet I är större än II

B: Kvantitet II är större än I

C: I är lika med II

D: Informationen är otillräcklig

Potenslagarna ger att kvantitet I är ${\left(\frac{7}{9}\right)}^2=\frac{49}{81}$ Slösa inte tid på att använda minsta gemensamma nämnare här, tiden för det saknas. Istället, jämför täljare med täljare och nämnare med nämnare. Täljaren är mindre i I än i II, medan nämnaren är större i I än i II. En större täljare och en mindre nämnare ger att II har fler bitar av en hel, där bitarna av den hela samtidigt är större. Alltså är II större än I. Svar: B

KVA: $\mathit{f}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{=}\mathbf{-}\mathbf{5}\mathit{x}\mathbf{+}\mathbf{20}$

Kvantitet I: $\frac{f\left(0\right)}{f(-1)}$

Kvantitet II: $\frac{f(-1)}{f\left(0\right)}$

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

Ett negativt k-värde innebär att funktionen lutar nedåt, sett från vänster till höger. Ett värde på x längre till vänster på tallinjen ger alltså ett större funktionsvärde än ett värde längre till höger. -1 är till vänster om 0, och ger därför ett större funktionsvärde än noll ger. Viktigt att notera är att båda funktionsvärdena är positiva. Ett stort (positivt) värde dividerat med ett litet (positivt) värde ger en kvot större än ett, medan ett litet värde dividerat med ett stort ger en kvot mindre än ett. Alltså är II större än I. Svar: B

KVA: 0 < x < y < 1

Kvantitet I: $\mathit{y}\mathbf{(}\mathbf{1}\mathbf{-}\mathit{x}\mathbf{)}$

Kvantitet II: $\mathit{x}\mathbf{(}\mathbf{1}\mathbf{-}\mathit{y}\mathbf{)}$

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

Utveckling av parenteserna ger att I = $y-xy$ och II = $x-xy$. Den högra termen, xy, är identisk, och därför blir det den första termens storlek som avgör. Ett stort tal minus något annat ger en större skillnad än ett litet tal minus något annat. Eftersom y är större än x måste kvantitet I vara större än II.

Svar: A

KVA: a och b är positiva heltal större än ett som uppfyller att ${\mathit{a}}^{\mathbf{b}\mathbf{ }}\mathbf{=}\mathbf{16}$. 

Kvantitet I: $b^a$

Kvantitet II: 16

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

De enda två möjliga talkombinationerna som är lika med sexton är $2^4$ och $4^2$. Det senare värdet fås lätt fram från de grundläggande kvadrattalen (1, 4, 9, 16, 25...), och det tidigare värdet fås genom att pröva sig fram. Börja på noll. Noll upphöjt i fyra är noll. Ett upphöjt i fyra är ett. Två upphöjt i fyra är sexton. 

Antingen är a = 2 och b = 4, eller är a = 4 och b = 2, men eftersom $a^b=b^a=16$ spelar det ingen roll vilken av alternativen det rör sig om, 16 = 16. Alltså är I = II. 

Svar: C

KVA: Kvantitet I: Resultatet då ett negativt tal subtraheras från noll

Kvantitet II: Resultatet då ett positivt tal subtraheras från noll

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

Här måste räknereglerna med negativa tal dras till minnes. Det gäller att:

$$\begin{gathered} ++=+ \\ +-=- \\ -+=- \\ --=+ \end{gathered}$$

Om detta känns abstrakt kan schemat fungera lättare.

• Alltid är positivt, aldrig är negativt
• Frisk är positivt, sjuk är negativt

Vilket ger följande möjligheter: 

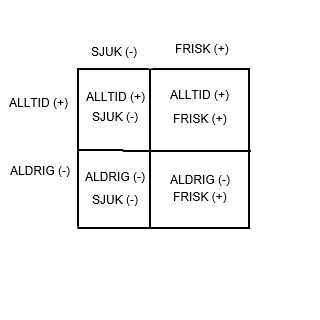Att alltid vara frisk är något positivt, medan det helt klart är negativt att alltid vara sjuk eller att aldrig vara frisk. Det kluriga är dock "aldrig sjuk". Det är två negativa ord, men tillsammans är det någonting positivt. Att subtrahera ett negativt tal från noll innebär alltså att addera noll till talet. Kvantitet I är positiv, medan kvantitet II är negativ, och alltså är I större än II. Svar: A

KVA:

$\mathit{y}\mathbf{\ne }\mathbf{0}$

$\frac{\mathbf{2}\mathbf{x}}{\mathbf{3}\mathbf{y}}\mathbf{=}\mathbf{4}$

Kvantitet I: x - 6y

Kvantitet II: 3

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

$\frac{2x}{3y}=4$

$2x=4·3y$

$2x=12y$

$x=6y$

Kvantitet I, x - 6y, är alltså samma som 6y - 6y = 0. 3, kvantitet II, är större än noll, och därmed är svaret B. 

KVA:

m och n är två på varandra följande heltal sådana att även $m-1$ och $n+1$ är två på varandra följande heltal. 

Kvantitet I: m

Kvantitet II: n

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

Det finns två olika möjligheter för m och n. Det ena alternativet är att m är mindre än n, och då måste $n=m+1$. Det skulle innebära att $n+1$ är samma sak som $m+2$, och därmed att skillnaden mellan m - 1 och n + 1 är tre. Att två på varandra följande tal skulle ha differensen tre är omöjligt. Alltså kan det inte gälla att m < n, utan m måste vara större än n. 

(Vi kan verifiera detta, genom att konstatera att om n < m, är m = n + 1, varpå m - 1 = n, och n +1 = m, vilka är två på varandra följande heltal.)

Svar: A.

KVA: 

$\mathbf{1}\mathbf{\le }\mathit{x}\mathbf{\le }\mathbf{4}$

$\mathbf{2}\mathbf{\le }\mathit{y}\mathbf{\le }\mathbf{6}$

$\mathbf{4}\mathbf{\le }\mathit{z}\mathbf{\le }\mathbf{8}$

Kvantitet I: Medelvärdet av x och y

Kvantitet II: Medelvärdet av y och z

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

Här lönar det sig att undersöka intervallen för de olika medelvärdena.

• Medelvärdet av x och y kan som minst vara medelvärdet mellan ett och två, vilket är 1,5. Som störst kan detta medelvärde vara medelvärdet mellan fyra och sex, vilket är 5. 
• Medelvärdet av y och z kan som minst vara medelvärdet mellan två och fyra, vilket är tre. Som max kan detta medelvärde vara medelvärdet mellan sex och åtta, vilket är sju.

Medelvärdena överlappar varandra i mitten. Om x = z = 4, är medelvärdena lika stora, oavsett värde på y. Om x är mindre än z är kvantitet II större än I. Alltså finns det inte tillräckligt med information för att besvara frågan.

Svar: D, informationen är otillräcklig.

KVA: Omkretsen av den regelbundna femhörningen ABCDE är 75 cm. 

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

Femhörningen är regelbunden, vilket innebär att alla sidor är lika långa, samt att vinklarna mellan varje sida är lika stora. Då det finns fem sidor, kommer varje sida att ha längden femton. Det är möjligt att räkna ut det exakta avståndet mellan A och D, men det stjäl tid. Istället kan informationen i uppgiften användas för att dra slutsatsen att figuren är korrekt ritad, och därifrån kan slutsatsen dras att sträckan AD är större än 15 cm. 

Svar: B, II är större än I.

KVA:

Kvantitet I: a + b 

Kvantitet II: b + c + d

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

Här behövs tre centrala kunskaper.

• Vinkelsumman i en fyrhörning är 360 grader.
• Motstående vinklar är lika stora när två parallella linjär skär varandra.
• Vinkelsumman i en triangel är 180 grader.

Eftersom vinkelsumman i en fyrhörning är 360 grader måste a + b vara 180 grader. Vinklarna i triangeln i figuren är motstående till vinklarna b, d och c. Därmed är vinklarna i triangeln också b, c och d, och vinkelsumman i en triangel är 180 grader. Det ger att b + c + d = 180 grader. Alltså är I och II lika stora. 

Svar: C

Edit: Vinklarna i triangeln är b, c och d, inget annat. 

NOG:

Hampus, Lena, Moa och Rickard är lärare. De undervisar alla i olika ämnen och varje lärare undervisar i endast ett ämne. Vilket ämne undervisar Moa i?

(1) Hampus eller Lena undervisar i naturkunskap. Moa eller Rickard undervisar i fysik.

(2) Hampus eller Rickard undervisar i engelska. Lena eller Moa undervisar i samhällskunskap. 

Tillräcklig information för lösningen erhålls 
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

(1) och (2): Det går snabbt att dra slutsatsen att inget av påståendena ensamt ger någon definit information om vilket ämne Moa undervisar i.

Tillsammans: Om informationen kombineras fås att:

Naturkunskap: Hampus eller Lena
Fysik: Rickard eller Moa
Engelska: Rickard eller Hampus
Samhällskunskap: Lena eller Moa

Här gäller det att identifiera om det skulle kunna finnas två (eller fler) olika svar. Då går uppgiften inte att lösa. Ponera att Hampus undervisar i naturkunskap, då måste Lena undervisa i samhällskunskap, Moa i fysik och Rickard i engelska. Det är ett korrekt svar, men säg att Hampus istället undervisar i engelska. Då måste Rickard undervisa i fysik, Moa i samhällskunskap, och Lena i naturkunskap. Det är också ett korrekt svar, och alltså kan uppgiften inte lösas.

Svar: E, ej genom de båda påståendena.

NOG:

Ett tyg säljs som metervara från en rulle. Hur många meter tyg finns det på rullen?

(1) Om affären säljer en femtedel av tyget på rullen och därefter en fjärdedel av återstoden av tyget så finns 60 procent av tyget kvar på rullen.

(2) Om affären säljer hälften av tyget på rullen och därefter en femtedel av återstoden av tyget så finns åtta meter tyg kvar på rullen.

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

(1): I detta påstående ges information om hur bitarna som säljs förhåller sig till varandra, men inget om hur mycket tyg det finns. Om tyget är en meter långt från början, eller etthundra meter, ger helt olika svar, och därför duger inte påstående ett.

(2): Här fås en uppgift om hur många meter tyg som är kvar på rullen, samt några instruktioner om hur stora de sålda bitarna är. Vi vet att när 50% av tyget, och sedan 20% av den kvarvarande biten är sålda, återstår åtta meter. Det går därmed att räkna ut med påstående två.

Svar: B, i (2) men ej i (1).

NOG:

Helena och Krister står 2,5 km från varandra efter samma raka väg. De startar samtidigt och cyklar mot varandra, var och en med sin egen konstanta hastighet. Med vilken hastighet cyklar Helena?

(1) Helena möter Krister efter 6 minuter

(2) Kristers hastighet är 15 km/h

(1): Denna tidsangivelse säger inget för sig själv. Om Krister cyklar med raketfart, och Helena mycket långsammare, kan det ta sex minuter för dem att mötas, men om de båda cyklar lika fort kan det också ta sex minuter för dem att mötas. Vi har två okända, men endast en ekvation. Därför duger inte (1) ensamt. 

(2): Denna tidsangivelse talar om hur snabbt Krister rör sig, men ingenting om när de möts. Om de möts efter tio sekunder eller två minuter medför helt olika värden på Helenas hastighet.

Tillsammans: Kristers tillryggalagda sträcka kan beräknas med hjälp av tiden i (1) och hastigheten i (2). Med hjälp av kunskaper om hur lång sträckan är kan även Helenas hastighet beräknas. 

Svar: C, i (1) tillsammans med (2).

NOG:

400 kvinnor och män fick frågan: Vad läser du oftast - kvällstidningen eller morgontidningen? 140 personer svarade kvällstidningen och resten svarade morgontidningen. Hur många män tillfrågades?

(1) 60 kvinnor svarade att de oftast läste kvällstidningen

(2) Det var lika många män som kvinnor som svarade att de oftast läste morgontidningen. 

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

(1): Detta påstående ger hur många män som oftast läste kvällstidningen, men inget om hur många som oftast läste morgontidningen. Om en man och 259 kvinnor svarade att de oftast läste morgontidningen, eller om det var en kvinna och 259 (eller några andra siffror) som svarade samma sak är oklart. Därför räcker inte (1) för att besvara frågan.

(2): Detta påstående ger ingen information om hur många män som svarade att de oftast läste kvällstidningen. Om det var en man och 139 kvinnor, eller en kvinna och 139 män framgår inte, och svaret är därför oklart. (2) räcker inte för att besvara frågan. 

Tillsammans: (1) ger information om hur många män som svarade att de oftast läste kvällstidningen, samt att (2) ger information om hur många män som svarade att de oftast läste morgontidningen. Tillsammans ger de alltså tillräckligt med information för att besvara frågan.

Svar: C, i (1) tillsammans med (2).

NOG: En klass ska utökas med 12 barn. Kan man därefter dela in klassen i grupper om 8 barn?

(1) Om klassen istället utökades med 4 barn så kan man dela in barnen i grupper om 8 barn.

(2) Innan klassen utökas är det inte möjligt att dela in barnen i grupper om 8 barn.

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

(1): Kalla antalet barn för b. Vi vet att $b+4$ är delbart med åtta. Till b adderas tolv, alltså $b+12$. Notera att:

$$\begin{gathered} b+12=b+4+8= \\ (b+4)+8 \end{gathered}$$

b + 4 kunde konstateras vara delbar med 8, och då kvarstår en åtta, som självklart är delbar med åtta. Slutsatsen blir att b + 12 är delbar med 8, och det är alltså möjligt att besvara frågan med påstående (1).

(2): Notera att vi endast behöver hitta två olika fall, ett där det är möjligt att dela in barnen i grupper om åtta, och ett där det inte är möjligt, för att bevisa att (2) inte räcker.

Om det var ett barn i klassen innan, skulle det inte gå att dela in barnen i grupper om åtta, men om det var fyra barn skulle det innebära att klassens storlek (efter utökningen) var 16 barn. 16 är delbart med 2. Alltså har vi hittat två exempel som ger olika slutsatser, och därmed är inte (2) tillräckligt för att svara på frågan.

Svar: A, i (1) men ej i (2).

NOG:

$\mathit{a}\mathbf{>}\mathit{b}$
$\mathit{b}\mathbf{>}\mathbf{0}$
$\mathit{k}\mathbf{=}\frac{\mathbf{a}}{\mathbf{b}}$

Vilket värde har k?

(1) a - b = 0

(2) $\frac{b}{a}=\frac{a}{b}$

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

(1): a - b = 0 kan arrangeras om till a = b. Det ger att värdet på k är ett. Påstående ett räcker således för att lösa uppgiften.

(2) Korsmultiplikation ger sambandet $a^2=b^2$. Eftersom $(-x{)}^2=x^2$ för alla tal x, kan vi inte direkt dra slutsatsen att a = b, men eftersom uppgiftsbeskrivningen utesluter alla negativa värden på a och b, kan slutsatsen dras att a = b, och därmed att k = 1. Informationen räcker för att besvara uppgiften. 

Svar: D, i (1) och (2) var för sig.

XYZ: Vilket av svarsalternativen är lika med uttrycket $\mathbf{2}\mathbf{(}\mathbf{-}\mathit{r}\mathbf{+}\mathbf{3}\mathit{s}\mathbf{)}$?

A: 3s - r + 2
B: -2r + 3s
C: 2(s - r) + s
D: $-6\left(\frac{r}{3}-s\right)$

Parentesen kan lösas ut och uttrycket blir $2(-r+3s)=-2r+6s$. Det ger att A och B direkt kan uteslutas. Även C kan uteslutas, eftersom svaret innehåller 3s, istället för det korrekta antalet, 6s. 

Svar: D.

XYZ: Vilken av graferna nedan representerar funktionen $\mathit{f}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{=}\frac{\mathbf{x}}{\mathbf{2}}\mathbf{+}\mathbf{2}$?

Den räta linjens ekvation ger att y = kx + m. I detta fall måste k alltså vara en halv, vilket är en positiv lutning. Därmed kan A och C direkt uteslutas. En rät linje med k-värdet ett växer lika snabbt i x-led som i y-led. Eftersom uppgiftsfunktionens k-värde är mindre än ett växer funktionen långsammare, och därmed är svaret D.

Svar: D.

XYZ: 12, a 17, 13 och 20 är fem positiva heltal som har medelvärdet 16. Vad är a?

A: 16
B: 18
C: 20
D: 22

Medelvärdet är summan av alla värden, dividerat med antalet värden.

$\frac{12+a+13+17+20}{5}=16$

$\frac{62+a}{5}=16$

$62+a=80$

$a=18$

Svar: B, a = 18.

XYZ: Linjen y = 5x + 10 skär x-axeln i punkten $(x_1, 0)$ och y-axeln i punkten $\left(0, y_1\right)$. Vad är $x_1+y_1$?

A: 5
B: 6
C: 8
D: 15

En rät linje skär y-axeln då x = 0, vilket motsvarar funktionens m-värde, vilket är 10. Det ger att $y_1=10$. Linjen skär även x-axeln då y-värdet är noll. Det ger ekvationen:

$0=5x_1+10$
$-5x_1=10$
$x_1=-2$

Summan av värdena är alltså 10 + (-2) = 8.

Svar: C, 8.

XYZ: $\frac{{\displaystyle \frac{\mathbf{3}}{\mathbf{2}}}}{{\displaystyle \frac{\mathbf{6}}{\mathbf{x}}}}\mathbf{=}\mathbf{2}$

Vad är x?

A: 4
B: 6
C: 8
D: 9

Bråket kan skrivas om till:

$\frac{3}{2}·\frac{x}{6}=2$
$\frac{3x}{12}=2$
$3x=24$
$x=8$

Svar: C, 8.

Vad är $\frac{\mathbf{5}}{\mathbf{2}}\mathbf{-}\frac{\mathbf{8}}{\mathbf{5}}\mathbf{?}$

A: -0,3
B: 0,9
C: 1,2
D: 1,7

Minsta gemensamma nämnare är 10, vilket ger uttrycket:

$$\begin{gathered} \frac{5}{2}-\frac{8}{5}= \\ \frac{5·5}{2·5}-\frac{8·2}{5·2}= \\ \frac{25}{10}-\frac{16}{10}=\frac{9}{10}=0,9 \end{gathered}$$

Svar: B, 0,9

XYZ: Vilket svarsalternativ har samma värde som ${\mathbf{5}}^{\mathbf{-}\mathbf{2}}\mathbf{-}{\left(\mathbf{-}\mathbf{2}\right)}^{\mathbf{-}\mathbf{1}}$?

A: $\frac{27}{50}$

B: $7^{-3}$

C: $\frac{2}{27}$

D: 27

Använd potenslagen som säger att $A^{-P}=\frac{1}{A^P}$. Det ger uttrycket 

$$\begin{gathered} \frac{1}{25}-\left(-\frac{1}{2}\right)= \\ \frac{1}{25}+\frac{1}{2} \end{gathered}$$

Vilket med hjälp av MGN kan räknas ut till 27 femtiondelar.

Svar: A.

XYZ: Vilket uttryck motsvarar ett heltal?

A: ${\left(\sqrt{7}+\sqrt{7}\right)}^2$

B: $7\sqrt{7}$

C: $\sqrt{7}+\sqrt{7}$

D. $\sqrt{7}+\sqrt{\frac{7}{7}}$

Regler angående irrationella tal:

• Addition av ett tal (rationellt eller irrationellt) till ett irrationellt tal förändrar inte rationaliteten. Ett irrationellt tal plus ett är fortfarande irrationellt.
• Multiplikation av ett irrationellt tal med ett heltal förändrar inte rationaliteten.

Med dessa två regler kan alternativ B, C och D direkt uteslutas. 

Svar: A.

XYZ: En rektangel är indelad i 15 mindre rektanglar. De mindre rektanglarna har alla samma area. Hur stor är arean av den skuggade delen av rektangeln? 

Arean av hela triangeln är $\frac{7}{5}\mathrm{cm}·1\mathrm{cm}=\frac{7}{5}{\mathrm{cm}}^2$. Det skuggade området är sex femtondelar av hela rektangeln. Det ger att den skuggade arean är (i kvadratcentimeter)

$$\begin{gathered} \frac{7}{5}·\frac{6}{15}= \\ \frac{7}{5}·\frac{2}{5}= \\ \frac{{\displaystyle 14}}{25} \end{gathered}$$

Svar: C.

XYZ: Hur stor är arean av fyrhörningen? 

Dela upp fyrhörningen i en övre och en undre triangel. Den övre triangeln har måtten 30 cm gånger 60 cm. Det ger en area på 900 kvadratcentimeter. Den undre triangeln har måtten 70 cm gånger 60 cm, vilket ger arean 2100 kvadratcentimeter. Den sammanlagda arean är alltså 3000 kvadratcentimeter. 

Svar: B.

XYZ: Vid ett möte skakade alla hand med varandra en gång. Det blev totalt 15 handskakningar. Hur många personer deltog i mötet?

A: 5
B: 6
C: 7
D: 8

Det krävs två personer för att skaka hand, och därmed måste två personer väljas ut från gruppen. Kalla antalet personer för x. Den första personen som väljs ut kan väljas ut på x olika sätt, och den andra på (x - 1) olika sätt. Då är antalet möjligheter $x(x-1)$. Här finns dock en hake, varje person skakar endast hand en gång med alla andra. Det innebär att "A hälsar på B" är samma sak som "B hälsar på A". Antalet möjliga kombinationer är alltså dubbelt så stort som antalet handskakningar. Det ger att:

$\frac{x(x-1)}{2}=15$

$x(x-1)=30$

Den som kan lösa andragradsekvationer kan använda valfri sådan metod, men annars är det lättaste att gissa. Om det är fem personer på mötet (A) fås $5·4\ne 30$. Om det var sex personer på mötet (B) fås $6·5=30$, vilket var vad vi letade efter! Svaret är alltså B.

XYZ: 

$p>0$
$p\ne r$
$r=\frac{k+p}{k}-1$

Vad är k?

A: k = 1
B: $k=\frac{p-1}{r-1}$

C: $k=\frac{P}{r+2}$

D: $k=\frac{P}{r}$

Skriv högerledet som ett bråk:

$r=\frac{k+p}{k}-1$
$r=\frac{k+p-k}{k}$

$r=\frac{p}{k}$

Lös ut k, och svaret blir $k=\frac{p}{r}$.

Svar: D

KVA: ${\mathit{x}}^{\mathbf{3}}\mathbf{<}\mathbf{0}$

Kvantitet I: $x^7$

Kvantitet II: $3x^4$

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

Ett negativt tal upphöjt till ett udda tal är negativt, men ett negativt tal upphöjt till ett jämnt tal blir ett positivt tal. Redan utan trean är därmed II större än I, och förstoringen gör detta ännu tydligare. 

Svar: B, II är större än I.

KVA: Samuel har en påse med endast röda, gröna och blå enfärgade kulor. 2/5 av kulorna är röda, och 3/10 av kulorna är gröna. Samuel plockar slumpmässigt upp en kula ur påsen.

Kvantitet I: Sannolikheten att kulan är blå

Kvantitet II: Sannolikheten att kulan är röd

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

Sannolikheten att kulan är röd är 2/5, enligt uppgiften. Eftersom det endast finns röda, blå och gröna kulor är sannolikheten att kulan är blå sannolikheten som uppfyller att:

$p_{röd}+p_{blå}+p_{grön}=1$
$\frac{2}{5}+\frac{3}{10}+p_{blå}=1$

Vilket med hjälp av minsta gemensamma nämnare fås till 3/10, vilket är mindre än 2/5. Alltså är svaret B.

Svar: B, II är större än I.

KVA: x > 0

Kvantitet I: $\frac{7x}{8}$

Kvantitet II: 88% av x

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

88% av x är samma sak som $0,88·x$. Frågan är alltså vad som är störst, sju åttondelar eller 0,88? En åttondel i procent kan fås som en halv fjärdedel, alltså hälften av 25%. En åttondel är alltså 12,5%. Sju åttondelar måste alltså vara 100% - 12,5% = 87,5%. Det medför att kvantitet II är större än I.

Svar: B, II är större än I.

KVA: De tre vinklarna i en triangel är u, v och w. 

Kvantitet I: u + v

Kvantitet II: w

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

I denna typ av uppgifter är det fördelaktigt att tänka på extremfall. Vad händer om vi har en triangel där u och v är väldigt små?

I denna triangel kommer kvantitet II att vara större än I, men vad skulle hända om exempelvis u och w bytte plats?

Då är kvantitet I större än II. Två olika svar innebär att det inte säkert kan sägas vilken av kvantiteterna som är störst.

Svar: informationen är otillräcklig. 

KVA: En affär har 75% rabatt på byxor och 70% rabatt på tröjor. Ordinarie pris för de röda byxorna är 299 kr. Ordinarie pris för den gula tröjan är 199 kr.

Kvantitet I: Det rabatterade priset för de röda byxorna

Kvantitet II: Det rabatterade priset för den gula tröjan.

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

75% rabatt av 299 kr är omständligt att räkna ut. 75% rabatt innebär att en fjärdedel av ursprungspriset kvarstår. En fjärdedel är samma sak som en halv halva, och priset kan avrundas till 300 kr. Hälften av 300 kr är 150 kr, och hälften av det är 75 kr. 

199 kr kan avrundas uppåt till 200 kr. 70% rabatt innebär att trettio procent av priset återstår. Det ger att priset för tröjan är $200·0,3$, dvs. 60 kr. 

Skillnaden mellan priserna är stora, och det är därför inte nödvändigt att ta hänsyn till avrundningen som gjorts i början. Svar: A, I är större än II.

KVA: $\sqrt{5}·\sqrt{9}={45}^x$

Kvantitet I: 0,5

Kvantitet II: x

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

• $\sqrt{a}·\sqrt{b}=\sqrt{a·b}$

Detta ger uttrycket:

$\sqrt{45}={45}^x$

• $a^{\frac{1}{2}}=\sqrt{a}$

Därmed kan slutsatsen dras att x = 0,5.

Svar: C, I är lika med II.

KVA:

Kvantitet I: $\frac{5}{3}-\frac{3}{2}$

Kvantitet II: $\frac{1}{7}+\frac{1}{42}$

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

Med hjälp av minsta gemensamma nämnare fås att kvantitet I är en sjättedel. Samma teknik plus förenkling ger att även kvantitet II är en sjättedel.

Svar: C, I är lika med II.

KVA: 

f(x) = y

Här gäller det att notera axlarnas graderingar. Den vänstra grafens x-axel hoppar två steg i taget, och ger att f(4) = 3. Den högra grafens y-axel hoppar också två steg i taget, vilket ger att g(3) = 6. 

Svar: B, II är större än I.

KVA: $30<3x-6<63$

Kvantitet I: x

Kvantitet II: 10

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

Addera 6 till alla led:

$36<3x<69$

Eftersom alla inblandade tal är positiva kan vi utan problem dividera alla led med tre (det går att dividera med negativa tal också, men då gäller särskilda regler för vad som händer med olikhetstecknen):

$12<x<23$

x kan alltså anta värden större än tolv, men mindre än 23. Oavsett värde på x är x alltid större än 10. 

Svar: A, I är större än II.

KVA: Radien i cirkeln C är x. Höjden i triangeln T är 2x och basen är 3x.

Arean av en cirkel är $\mathrm{\pi }·r^2$, och arean av en triangel är $\frac{bh}{2}$. Det ger att cirkelns area är $\mathrm{\pi }{x}^2$, och triangelns area är $3x^2$. Frågan är alltså vilket tal som är större, 3 eller $\mathrm{\pi }$? Pi är ju något i stil med 3,14, vilket är större än tre. 

Svar: A, I är större än II.

NOG: I en låda finns det fyra olika sorters spik: nubb, kopparspik, pappspik och dyckert. Hur många spikar finns det i lådan?

(1) I lådan finns det 24 kopparspikar, vilket är 50% mer än antalet dyckertar.

(2) Dyckert och kopparspik utgör tillsammans 50% av antalet spikar i lådan. 

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

(1): Detta påstående berättar hur många kopparspikar och dyckertar som finns i lådan, men inget om de andra sorterna. Denna information räcker därför inte.

(2): Detta påstående berättar att pappspik och nubbar tillsammans utgör 50% av innehållet, men säger ingenting om antalet. Denna information räcker inte.

Tillsammans: I (1) fås hur många kopparspikarna och dyckertarna är, och i (2) fås att detta är hälften av alla spikar i lådan. Alltså räcker dessa två påståenden tillsammans för att bestämma antalet spikar. 

Svar: C, i (1) tillsammans med (2).

NOG: Var och en av Mimmis tröjor är antingen färgglad eller svart. Varje tröja är dessutom antingen långärmad eller kortärmad. Mimmi har 14 långärmade tröjor. Hur många tröjor har Mimmi?

(1) Hälften av de färgglada tröjorna är långärmade.

(2) Sex av de svarta tröjorna är inte långärmade

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

Ett förslag för att snabbt få en översikt är att göra en tabell över situationen: 

(1) ger inte tillräckligt med information, eftersom vi inte vet något om de svarta tröjorna. (2) ger inte heller tillräckligt med information, eftersom vi inte vet något om de färgglada tröjorna. 

Tillsammans:

Det totala antalet långärmade tröjor är 14 st. och eftersom det inte finns någon information om antalet färgglada tröjor, går det inte att lösa uppgiften. 

Svar: E, ej genom de båda påståendena.

NOG: Bland talen 28, 32, 42, 56, 72 och 78 väljs ett tal ut, vilket?

(1) Talet är jämnt delbart med 3.

(2) Talet är en heltalsmultipel av 4.

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

(1): De tal som uppfyller detta har en siffersumma delbar med tre. Det är 42, 72 och 78, vilket är flera olika svar, och därför räcker inte (1) ensamt.

(2). De tal som uppfyller detta är tal delbara med fyra, vilket är 28, 32 och 72. Det är återigen flera olika svar, och därför räcker inte (2) ensamt. 

Tillsammans: Det enda gemensamma talet i (1) och (2) är 72. Ett entydigt svar innebär att uppgiften går att lösa. 

Svar: C, i (1) tillsammans med (2).

NOG: Två löpare springer ett antal varv runt samma motionsslinga. Båda löparna startar samtidigt från samma plats. De springer åt samma hål, var och en med sin egen konstanta hastighet. Efter hur lång tid blir den långsammare löparen varvad av den snabbare löparen?

(1) Slingan är 800 meter lång och det tar den långsammear löparen 6 minuter att springa ett varv runt slingan. 

(2) Efter 9 minuter har den långsammare löparen sprungit ett och ett halvt varv runt slingan, vilket är 1200 meter. Samtidigt har den snabbare löparen sprungit 2000 meter. 

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

(1): Detta säger inget om den snabbare löparens hastighet. Om den snabbare löparen springer i raketfart eller bara en meter per sekund snabbare än den långsammare, framgår inte, och därmed kan uppgiften inte lösas med denna information.

(2): Detta påstående ger information om den långsammare och den snabbare löparens hastighet, via $s=v·t$-formeln. Dessutom ges information om slingans längd. Då kan tiden det tar tills den långsammare löparen blir varvad beräknas.

Svar: B, i (2) men ej i (1).

NOG: Vad är 15 procent av y?

(1) y är 60 procent av 900

(2) 5 procent av y är 27

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

(1): Detta påstående ger information om en andel, samt någonting om dess absoluta storlek. y är 60 procent av 900. Det innebär att vi kan ställa upp ekvationen $y=0,60·900$, vilket går att lösa.

(2): Detta påstående ger information om den absoluta storleken av en given andel av y. Det medför att vi kan ställa upp ekvationen $0,05·y=27$, vilket går att lösa.

Svar: D, i (1) och (2) var för sig.

NOG: Tre enfärgade klossar - en röd, en grön och en blå - är staplade på varandra. Vilken färg har den översta klossen?

(1) Den blå klossen är inte underst. Den gröna klossen är inte överst.

(2) Den röda klossen är inte i mitten. Den blå klossen är under den röda klossen. 

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

(1): Vilka möjliga alternativ finns som uppfyller dessa krav?

Blå, Röd, Grön
Blå, Grön, Röd
Röd, Blå, Grön

Den blå eller den röda klossen kan vara överst, vilket medför att en definit lösning är omöjlig endast med (1).

(2): Vilka alternativ finns som uppfyller dessa krav?

Röd, Blå, Grön
Röd, Grön, Blå

Eftersom det ska finnas en blå kloss under den röda, kan den röda klossen inte vara underst. Den får inte heller vara i mitten. Den översta klossen kan således endast vara röd, och därmed kan frågan besvaras.

Svar: B, i (2) men ej i (1).

DTK: 

Hur stor andel av kommunernas totala utgifter för kultur 2010 utgjorde utgifterna för musik- och kulturskolor?

A: 20 procent
B: 30 procent
C: 40 procent
D: 50 procent

Slösa inte tid på att försöka läsa av hur mycket pengar varje aktivitet kostade. Mät istället staplarnas längder, och räkna ut musik- och kulturskolornas andel genom att dividera deras längd med den totala längden. Då fås att svaret är 20%.

Svar: A, 20%.

DTK: (se ursprungsbilden i ovanstående inlägg)

Hur stora var kommunernas sammanlagda utgifter för stöd till studieorganisationer under de redovisade åren?

A: 4 600 miljoner kr
B: 5 400 miljoner kr
C: 6 600 miljoner kr
D: 7 200 miljoner kr

Denna utgiftskategori är nästan konstant i intervallet. Dra en linje som motsvarar det ungefärliga genomsnittet, och beräkna antalet år multiplicerat med denna kostnad:

$500·11=5 500$ (miljoner kr)

Svarsalternativ B är 5 400 miljoner kr, vilket stämmer bra. 

Svar: B, 5 400 miljoner kronor.

Kommentar: Svaret skulle också kunna vara A, eftersom frågan ber om de "redovisade åren". I diagrammet finns endast nio redovisade år. Men detta är facits variant.

DTK: (se originaldiagrammet i ovanstående inlägg)

För vilket kulturområde hade kommunernas utgifter förändrats minst, procentuellt sett, om man jämför det första och det sista redovisade året?

A: Stöd till studieorganisationer
B: Musik- och kulturskolor
C: Bibliotek
D: Allmän kulturverksamhet

Rita i diagrammet! En linje för det första året i varje kategori, och en streckad linje för det sista året i varje kategori ger:

Den totala förändringen för alla kategorier utom biblioteken är nästintill identisk. Eftersom den allmänna kulturverksamhetens staplar är mycket större än både studieorganisationernas och musik- och kulturskolornas, kommer denna ökning att vara mycket mindre procentuellt sett. Därför kan alternativ A och B strykas direkt.

Frågan är då om svar C eller D är korrekt. Tydligt är att C har ökat mycket mer än D, samt att C från början var mycket mindre än D. Det innebär att C:s förändring kommer att vara mycket större än D:s procentuellt sätt. Alltså är svaret D, allmän kulturverksamhet.

DTK: Vilket svarsförslag stämmer bäst överens med de väderdata som redovisas för den 4 februari?

A: Vindstyrkan varierade mellan 3 m/s och 6 m/s.
B: Vinden var i huvudsak nordostlig
C: Temperaturen varierade mellan -12 °C och -5 °C
D: Nederbörden var 2,1 mm.

Det regnade överhuvudtaget inte den fjärde februari, och vinden var främst sydlig. Där försvinner alternativ D och B. Temperaturen nådde knappt ned till -12 °C, vilket utesluter alternativ C. 

Svar: A, vindstyrkan varierade mellan 3 m/s och 6 m/s.

DTK: (se originaldiagrammet i ovanstående inlägg)

Vilken var medeltemperaturen för de åtta dygnen?

A: +2 °C
B: -1 °C
C: -4 °C
D: -7 °C

Det går att räkna ut detta, men tiden för det saknas. Istället är det bättre att markera ut varje alternativ i diagrammet:

Om arean ovanför linjen är lika stor som arean under linjen, har vi hittat medelvärdet. A och D går bort omedelbart. Det står alltså mellan -1 °C och -4 °C. Alternativ B ser rimligt ut, men vid första till fjärde februari går temperaturen ned rejält, vilket drar med sig medeltemperaturen ned. -4 °C är det alternativ vars areor ovanför och under grafen är jämnast, och därför är svaret C, 4 °C.

DTK: (ursprungsdiagrammet finns i ovanstående inlägg)

Hur många av dygnen noterades nederbörd respektive rakt sydlig vind?

A: 3 respektive 1 dygn
B: 3 respektive 3 dygn
C: 4 respektive 1 dygn
D: 4 respektive 3 dygn

Här är det bara att räkna dagarna:

Fyra dagar med nederbörd, samt tre dagar med rakt sydlig vind. Svar: D, 4 respektive 3 dygn.

DTK:

Studera skillnaden mellan den övre och den undre kvartilen bland dem med examensår 1980-1984. Inom vilken utbildningsriktning återfanns den största skillnaden, i kronor räknat?

A: Ekonomer
B: Personalvetare
C: Samhällsvetare
D: Socionomer

För ekonomer är skillnaden 11 000, för personalvetare är skillnaden drygt 18 000 kr, för samhällsvetare är skillnaden ca. 6 000 kr, och för socionomer är skillnaden 11 000 kr. Svaret är alltså B, personalvetare.

DTK: (originaltabellerna finns i ovanstående inlägg)

Vilken var medellönen per månad inom den utbildningsriktning som omkring en fjärdedel av samtliga 2 370 svarande tillhörde?

Beteendevetare: 257 av 2 370 är långt ifrån 25%
Ekonomer: 181 av 2 370 är långt ifrån 25%
Personalvetare: 550 av 2 370 är nära 25%, detta är ett möjligt alternativ.
Samhällsvetare: 220 av 2 370 är långt ifrån 25%
Socionomer: 880 av 2370 är en bit ifrån 25%. 

Det alternativ som är närmast är alltså personalvetarna. Deras medellön var 36 010 kr. 
Svar: D, 36 010 kr.

DTK: (originaltabeller finns i ovanstående inlägg)

I vilket av följande län hade mer än hälften högre lön än medellönen för länet?

A: Gotlands län
B: Örebro län
C: Dalarnas län
D: Västerbottens län

Vad innebär egentligen frågan? Mer än hälften av de svarande har en högre lön än medellönen. Det låter först omöjligt, men det kan ske om en liten grupp (mindre än hälften) tjänar mycket mindre än den större gruppen (över hälften). Medellönen dras då ned av denna grupp, och de mittersta personerna tjänar mer än medellönen. Detta innebär att medianen kommer att vara högre än medellönen för denna grupp. En snabbtitt i diagrammet visar:

Det enda län med en medianlön högre än medellönen är Örebro län. Svaret är därför B, Örebro.

DTK: (originaltabellerna finns i ovanstående inlägg)

Hur mycket högre var medellönen bland ekonomerna med examensår 1995 - 1999 än bland beteendevetarna med examen från samma period?

A: 15 procent högre
B: 25 procent högre
C: 35 procent högre
D: 45 procent högre

Ekonomernas lön var 41 000 kr, medan beteendevetarnas lön var 33 000 kr. 

$\frac{41 000}{33 000}=\frac{41}{33}\approx \frac{20}{16}=\frac{5}{4}=1,25$

Ekonomernas lön var ungefär 1,25 gånger beteendevetarnas. Det innebär att deras lön var 25 procent högre.

Svar: B, 25 procent högre

DTK: 

Hur många hamnområden exporterade minst 400 000 ton papper?

A: 3
B: 4
C: 5
D: 7

Minst 400 000 ton innefattar den medelstora och den stora varianten av den gråa pilen. Eftersom det rör sig om export ska pilen vara riktad bort från kusten. Totalt finns fem pilar som uppfyller dessa krav.

Svar: C, 5.

DTK: (originalbild finns i ovanstående inlägg)

Vilket hamnområde avses?

Importen av trä var minst 800 000 ton och exporten av trä var 40 000 - 399 000 ton. Hamnområdet exporterade även 400 000 - 800 000 ton pappersmassa.

A. Haparanda - Skellefteå
B: Umeå - Sundsvall
C: Hudiksvall - Gävle
D: Västervik - Kalmar.

Alla områden importerade denna mängd trä, men Hudiksvall - Gävle samt Umeå - Sundsvall exporterade inte rätt mängd trä. Alltså kan alternativ C och B uteslutas.

Haparanda - Skellefteå exporterade för lite pappersmassa, och därför kan alternativ A uteslutas.

Svar: D, Västervik - Kalmar.

DTK: 

Hur stort var antalet anmälda fall av skadegörelse i genomsnitt per år för den redovisade perioden?

A: 155 000
B: 165 000
C: 175 000
D: 185 000

Att räkna ut genomsnittet är möjligt, men tar för mycket tid. Rita istället ut en linje för varje svarsalternativ, och använd uteslutningsmetoden. Arean ovanför och under linjen ska vara lika stor för att linjen ska visa genomsnittet. Alternativ A och D är fullständigt orimliga och kan uteslutas direkt. Även alternativ C kan uteslutas med lite eftertanke; kullen vid år 2008-09 är mycket mindre än dalen från 2002 till 2008. Alltså kan C inte vara rätt.

Svar: B, 165 000.

DTK: (originaldiagram i ovanstående inlägg)

Hur många cykelstölder anmäldes sammanlagt under 2006 - 2009?

A: 200 000
B: 230 000
C: 270 000
D: 300 000

I diagrammet är antalet cykelstölder under de givna åren nästan konstant: 

Ett ungefärligt genomsnitt är 68 000 per år, i fyra år. $68 000·4=272 000$, vilket passar utmärkt med svarsalternativ C.

Svar: C, 270 000.

DTK: (originaldiagram i ovanstående inlägg)

Hur stor var den procentuella minskningen av antalet anmälda bilbrott om man jämför den redovisade periodens första och sista år?

A: 40 procent
B: 50 procent
C: 60 procent
D: 70 procent

$\frac{85 000}{210 000}=\frac{85}{210}\approx \frac{42}{105}\approx 40\%$

Bilbrotten år 2011 är drygt 40% av antalet bilbrott år 2002. Det är en minskning med 60%. 

Svar: C, 60 procent.

DTK:

Kartan är indelad i fyra lika stora fält, som efter väderstrecken kan benämnas nordväst, nordost, sydost och sydväst. Vilken bergart förekommer i samtliga fält utom det nordöstra?

A: Migmatitgranit
B: Metaryolit
C: Dalagranit
D: Migmatitomvandlat metasediment

Ett knep för att spara tid är att undersöka om vilka tre svarsalternativ som finns i det nordöstra fältet. Om tre alternativ kan identifieras i detta fält kan de uteslutas, och ett svar har nåtts. (Om tre av alternativen inte kan identifieras i det nordöstra fältet måste dock de andra fälten undersökas)

Den enda bergart som inte förekommer i fältet är Migmatitgranit, vilket innebär att det är svaret.

Svar: A, Migmatitgranit.

DTK: (originalkarta finns i ovanstående inlägg)

Vad av följande finns 2,5 mil i sydvästlig riktning från Mansjön?

A: Polymorfisk granit
B: Kvartit
C: Migmatitomvandlat metasediment
D: Finnsjön

Använd en linjal och skalan längst ned till höger för att mäta upp 2,5 mil sydväst. Då landar linjen i ett stort, vitt fält. Det vita fältet motsvarar Äldre granitoider, vilket inte är ett alternativ. Det enda som finns i fältet förutom dessa gratinoider är Finnsjön, vilket finns som alternativ. 

Svar: D, Finnsjön.

DTK: (ursprungskarta i ovanstående inlägg)

Utgå från den nordligaste änden av den regionala deformationszon som i söder börjar en kilometer från tätorden Edsbyn. Fortsätt till närmast belägna plats till migmatitgranit. Gå därifrån vidare till närmaste tätord. Hur långt är det mellan den tätorten och Loos koboltgruva?

A: 15 km
B. 45 km
C: 55 km
D: 75 km

Börja med att identifiera tätorden Edsbyn på kartan. De regionala deformationszonerna betecknas med en linje. Följ linjen norrut till slutet av zonen. Det närmaste området med migmatitgranit ligger då sydväst. 

Den närmaste tätorten är Voxna. Avståndet från Voxna till Loos koboltgruva (grönt) är ca. 9 cm, vilket motsvarar 45 km enligt kartan. 

Svar: C, 45 km.

DTK: 

Vilket svarsförslag anger proportionen mellan antalet 50-öringar, 1-kronor, 5-kronor och 10-kronor som har präglats med årtalet 2008?

Antalet femtioöringar är strax över hälften av antalet enkronor. Dessutom är antalet fem- och tiokronor en femtedel av antalet enkronor. Svarsalternativet måste alltså vara X:5:1:1. De alternativ som fungerar är då A och B, och eftersom antalet femtioöringar var strax över hälften av antalet enkronor måste B vara svaret. 

Svar: B, 3:5:1:1

DTK: (originaltabell i ovanstående inlägg)

Med vilket av följande årtal har cirka 100 miljoner mynt präglats?

A: 2000
B: 2003
C: 2007
D: 2009

• År 2000 (A) präglades över en miljon enkronor ensamt, vilket utesluter alternativ A. 
• År 2003 (B) kan det totala antalet mynt summeras till drygt 111 miljoner, vilket är för mycket och utesluter alternativ B.
• År 2009 (D) var antalet präglade mynt inte ens i närheten av 100 miljoner, vilket utesluter alternativ D.

Det enda alternativ som kvarstår är C, 2007. Den som har tid över kan kontrollräkna, men det är inget måste.

DTK: (ursprungstabell i ovanstående inlägg)

Bestäm det årtal som flest mynt har präglats med. Hur stor andel av mynten med detta årtal utgörs av 1-kronor?

A: 50 procent
B: 60 procent
C: 70 procent
D: 80 procent

Det år då flest mynt präglades är år 2000, bland annat på grund av det höga antalet enkronor. År 2000 präglades drygt 153 miljoner mynt, varav 107 miljoner mynt var enkronor. Det ger procentsatsen:

$\frac{107}{153}\approx \frac{105}{150}\approx 70\%$

Avrunda 107 till 100, och 153 till 150. Då fås att andelen enkronor var drygt 2/3, alltså ungefär 67%. Eftersom vi avrundade nedåt något i början är det dock viktigt att avrunda uppåt något, vilket ger svaret 70%, C. (Vid avrundning av 67% blir svaret 70% ändå, men denna kommentar ger svaret extra trovärdighet)

Svar: C, 70%

DTK: 

Hur många fler förlossningar skedde bland kvinnor 33–35 år än bland kvinnor 36–38 år?

A: 20
B: 25
C: 35
D: 40

De lägsta staplarna börjar vid 90, varför det är smart att börja räkna därifrån. Staplarna för 34 och 37 är i princip lika höga; 34-stapeln är kanske två graviditeter större. Det som är intressant är skillnaden mellan stapelgrupperna, inte deras individuella storlekar. Därför kan 34-stapeln räknas som två graviditeter och 37-stapeln som noll.  33-stapeln kan avläsas till att innehålla 30 graviditeter (ovanför strecket), och 35-stapeln drygt tolv. I den äldre gruppen står 36-stapeln för ungefär fem graviditeter (ovanför 90-strecket).

Det medför att, ovanför 90-strecket, finns 12 + 2 + 30 = 44 graviditeter i den yngre gruppen. Det fanns sammanlagt fem graviditeter i den äldre gruppen (när 37-stapeln nollställts mot 34-stapeln). Det ger en skillnad på 39 graviditeter.

Svar: D, 40.

DTK: (se originalbild i ovanstående inlägg)

Hur stor var skillnaden avseende andelen förlossningar per startad behandlingscykel om man jämför 30-åringar med 40-åringar?

A: 16 procentenheter
B: 20 procentenheter
C: 32 procentenheter
D: 42 procentenheter

I 30-gruppen är procenten strax under 32%, och i 40-gruppen är procenten ungefär 16%. Det ger en skillnad på drygt femton procentenhet. Därför är svaret A, 16 procentenheter.

DTK: (se originalbild i ovanstående inlägg)

För vilken ålder gällde att det skedde 20 förlossningar och att andelen förlossningar per startad behandlingscykel var 10 procent?

A: 25 år
B: 26 år
C: 41 år
D: 42 år

Börja med antalet graviditeter. De åldersgrupper som uppfyller detta, samt finns som alternativ, är 25 och 41 år. 25 ligger dock skyhögt över 10 procent avseende behandlingscykler. Därför är svaret C, 41 år. 

Jag hinner inte kommentera just nu på varje fråga som jag har missat under HP -det blev några stycken- (men när jag såg svaren tänkte jag, såklart!!)

Och hittar inte förra året kattungen, så jag lånar Mark Mansons.

Men en än gång, Smutstvätt:

Smutstvätt skrev:

KVA: 

$\mathbf{1}\mathbf{\le }\mathit{x}\mathbf{\le }\mathbf{4}$

$\mathbf{2}\mathbf{\le }\mathit{y}\mathbf{\le }\mathbf{6}$

$\mathbf{4}\mathbf{\le }\mathit{z}\mathbf{\le }\mathbf{8}$

Kvantitet I: Medelvärdet av x och y

Kvantitet II: Medelvärdet av y och z

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

---

Här lönar det sig att undersöka intervallen för de olika medelvärdena.

• Medelvärdet av x och y kan som minst vara medelvärdet mellan ett och två, vilket är 1,5. Som störst kan detta medelvärde vara medelvärdet mellan fyra och sex, vilket är 5. 
• Medelvärdet av y och z kan som minst vara medelvärdet mellan två och fyra, vilket är tre. Som max kan detta medelvärde vara medelvärdet mellan sex och åtta, vilket är sju.

Medelvärdena överlappar varandra i mitten. Om x = z = 4, är medelvärdena lika stora, oavsett värde på y. Om x är mindre än z är kvantitet II större än I. Alltså finns det inte tillräckligt med information för att besvara frågan.

Svar: D, informationen är otillräcklig.

Är det inte en (om än väldigt liten) tidsfälla att beräkna medelvärdena? Man kan ju nöja sig med

$$\begin{gathered} 3\le x+y\le 10 \\ 6\le y+z\le 14 \end{gathered}$$

och se att de delar intervallet 6-10.

Två inlägg senare: Du säger a, b och c när du antagligen menar b, c och d.

Tack igen för delade insikter!

pelleplums skrev:

Smutstvätt skrev:

KVA: 

$\mathbf{1}\mathbf{\le }\mathit{x}\mathbf{\le }\mathbf{4}$

$\mathbf{2}\mathbf{\le }\mathit{y}\mathbf{\le }\mathbf{6}$

$\mathbf{4}\mathbf{\le }\mathit{z}\mathbf{\le }\mathbf{8}$

Kvantitet I: Medelvärdet av x och y

Kvantitet II: Medelvärdet av y och z

A: Kvantitet I är större än II
B: Kvantitet II är större än I
C: I är lika med II
D: Informationen är otillräcklig

---

Här lönar det sig att undersöka intervallen för de olika medelvärdena.

• Medelvärdet av x och y kan som minst vara medelvärdet mellan ett och två, vilket är 1,5. Som störst kan detta medelvärde vara medelvärdet mellan fyra och sex, vilket är 5. 
• Medelvärdet av y och z kan som minst vara medelvärdet mellan två och fyra, vilket är tre. Som max kan detta medelvärde vara medelvärdet mellan sex och åtta, vilket är sju.

Medelvärdena överlappar varandra i mitten. Om x = z = 4, är medelvärdena lika stora, oavsett värde på y. Om x är mindre än z är kvantitet II större än I. Alltså finns det inte tillräckligt med information för att besvara frågan.

Svar: D, informationen är otillräcklig.

Är det inte en (om än väldigt liten) tidsfälla att beräkna medelvärdena? Man kan ju nöja sig med

$$\begin{gathered} 3\le x+y\le 10 \\ 6\le y+z\le 14 \end{gathered}$$

och se att de delar intervallet 6-10.

Två inlägg senare: Du säger a, b och c när du antagligen menar b, c och d.

Tack igen för delade insikter!

Wow, du lusläser verkligen, vad roligt! :) Vad det gäller att beräkna medelvärdet tar det lite längre tid, men det är en beräkning som det är vanligare att man är van vid om man inte kan så mycket matematik. Om man känner sig bekväm med att multiplicera olikheter, går det alldeles utmärkt att göra som du skriver. Mycket bra tips!

Angående det andra inlägget är det helt korrekt att jag slarvat. Det ska genast rättas till! :)

Smutstvätt skrev:

NOG:

Ett tyg säljs som metervara från en rulle. Hur många meter tyg finns det på rullen?

(1) Om affären säljer en femtedel av tyget på rullen och därefter en fjärdedel av återstoden av tyget så finns 60 procent av tyget kvar på rullen.

(2) Om affären säljer hälften av tyget på rullen och därefter en femtedel av återstoden av tyget så finns åtta meter tyg kvar på rullen.

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

---

(1): I detta påstående ges information om hur bitarna som säljs förhåller sig till varandra, men inget om hur mycket tyg det finns. Om tyget är en meter långt från början, eller etthundra meter, ger helt olika svar, och därför duger inte påstående ett.

(2): Här fås en uppgift om hur många meter tyg som är kvar på rullen, samt några instruktioner om hur stora de sålda bitarna är. Vi vet att när 50% av tyget, och sedan 20% av den kvarvarande biten är sålda, återstår åtta meter. Det går därmed att räkna ut med påstående två.

 

Svar: B, i (2) men ej i (1).

 

Hej, 

Informationsdel 1 ger ekvationen 4/5x*3/4= 6/10x  , här har vi en variabel och en  ekvation så det borde gå att lösa ekvationen. Men när man testar så ser man att det inte går att lösa ekvationen och att informationen är ej tillräckligt. På NOG uppgifter brukar jag inte lösa uppgiften utan jag bara kolla om det finns lika många oberoende ekvationer som okända variabler då tar jag slutsatsen att det gåår  eller inte att besvara frågan. Min fråga är när vi har lika många variabler som oberoende ekvationer men det ändå inte går att lösa ekvationer, hur ska man veta att det om man inte vill lösa uppgiften och spara tid?? 

Utmärkt fråga! Det stämmer att vi har en ekvation med en obekant, men problemet är ekvationen i sig. Om vi förenklar ekvationen $\frac{4}{5}x·\frac{3}{4}=\frac{6}{10}x$ får vi: 

$$\begin{gathered} \frac{4}{5}x·\frac{3}{4}=\frac{6}{10}x \\ \frac{4·3}{5·4}x=\frac{6}{10}x \\ \frac{12}{20}x=\frac{6}{10}x \\ \frac{6}{10}x=\frac{6}{10}x \end{gathered}$$

Denna ekvation är alltså en tautologi, eller ett påstående som alltid är sant. 

Vi kan se detta från påståendet, eftersom påståendet endast pratar om andelar. Först säljer vi en femtedel av tyget, och sedan en fjärdedel, och då återstår ännu en andel. Vi behöver någon form av information i meter snarare än andelar, för att kunna säga något om mängden tyg på rullen. :)

Smutstvätt skrev:

NOG:

Ett tyg säljs som metervara från en rulle. Hur många meter tyg finns det på rullen?

(1) Om affären säljer en femtedel av tyget på rullen och därefter en fjärdedel av återstoden av tyget så finns 60 procent av tyget kvar på rullen.

(2) Om affären säljer hälften av tyget på rullen och därefter en femtedel av återstoden av tyget så finns åtta meter tyg kvar på rullen.

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

---

(1): I detta påstående ges information om hur bitarna som säljs förhåller sig till varandra, men inget om hur mycket tyg det finns. Om tyget är en meter långt från början, eller etthundra meter, ger helt olika svar, och därför duger inte påstående ett.

(2): Här fås en uppgift om hur många meter tyg som är kvar på rullen, samt några instruktioner om hur stora de sålda bitarna är. Vi vet att när 50% av tyget, och sedan 20% av den kvarvarande biten är sålda, återstår åtta meter. Det går därmed att räkna ut med påstående två.

Svar: B, i (2) men ej i (1).

Hej, varför får man fel svar om man tänker att informationsdel 2 säger att man ska först ta 50% av tyget och då kvarstår 50% av det hela men sedan tar man bort 20% av 50% som vi hade kvar. Alltså 50%-20% =30% , så har vi bara 30% av tyget och det ska vara lika med 8 meter. 3/10* L = 8  , det ger L= ca 26 m. Men det är fel. Svaret ska bli 20 m . 

Smutstvätt skrev:

NOG:

Ett tyg säljs som metervara från en rulle. Hur många meter tyg finns det på rullen?

(1) Om affären säljer en femtedel av tyget på rullen och därefter en fjärdedel av återstoden av tyget så finns 60 procent av tyget kvar på rullen.

(2) Om affären säljer hälften av tyget på rullen och därefter en femtedel av återstoden av tyget så finns åtta meter tyg kvar på rullen.

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

---

(1): I detta påstående ges information om hur bitarna som säljs förhåller sig till varandra, men inget om hur mycket tyg det finns. Om tyget är en meter långt från början, eller etthundra meter, ger helt olika svar, och därför duger inte påstående ett.

(2): Här fås en uppgift om hur många meter tyg som är kvar på rullen, samt några instruktioner om hur stora de sålda bitarna är. Vi vet att när 50% av tyget, och sedan 20% av den kvarvarande biten är sålda, återstår åtta meter. Det går därmed att räkna ut med påstående två.

Svar: B, i (2) men ej i (1).

Hej, varför får jag fel svar. Informations del 2 säger att först säljer man 50% av tyget och sedan 20% av tyget och det som kvar är lika med 8 meter. Det betyder att 50%-20% = 30% , 30%*L = 8 

Alltså 3/10 * L = 8 och när jag löser ekvationen så får jag L blir ca 26m . Men det är fel. Svaret ska bli 20m. Varför mitt tänkesätt är fel? 

Smutstvätt skrev:

NOG: En klass ska utökas med 12 barn. Kan man därefter dela in klassen i grupper om 8 barn?

(1) Om klassen istället utökades med 4 barn så kan man dela in barnen i grupper om 8 barn.

(2) Innan klassen utökas är det inte möjligt att dela in barnen i grupper om 8 barn.

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

---

(1): Kalla antalet barn för b. Vi vet att $b+4$ är delbart med åtta. Till b adderas tolv, alltså $b+12$. Notera att:

$$\begin{gathered} b+12=b+4+8= \\ (b+4)+8 \end{gathered}$$

b + 4 kunde konstateras vara delbar med 8, och då kvarstår en åtta, som självklart är delbar med åtta. Slutsatsen blir att b + 12 är delbar med 8, och det är alltså möjligt att besvara frågan med påstående (1).

(2): Notera att vi endast behöver hitta två olika fall, ett där det är möjligt att dela in barnen i grupper om åtta, och ett där det inte är möjligt, för att bevisa att (2) inte räcker.

Om det var ett barn i klassen innan, skulle det inte gå att dela in barnen i grupper om åtta, men om det var fyra barn skulle det innebära att klassens storlek (efter utökningen) var 16 barn. 16 är delbart med 2. Alltså har vi hittat två exempel som ger olika slutsatser, och därmed är inte (2) tillräckligt för att svara på frågan.

Svar: A, i (1) men ej i (2).

Hur kunde man veta att det går att lösa uppgiften med informations del1, om man inte tänker på att 12 är 8+4 ??? Tacksam om någon svarar! 

I am Me skrev:

Smutstvätt skrev:

NOG:

Ett tyg säljs som metervara från en rulle. Hur många meter tyg finns det på rullen?

(1) Om affären säljer en femtedel av tyget på rullen och därefter en fjärdedel av återstoden av tyget så finns 60 procent av tyget kvar på rullen.

(2) Om affären säljer hälften av tyget på rullen och därefter en femtedel av återstoden av tyget så finns åtta meter tyg kvar på rullen.

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

---

(1): I detta påstående ges information om hur bitarna som säljs förhåller sig till varandra, men inget om hur mycket tyg det finns. Om tyget är en meter långt från början, eller etthundra meter, ger helt olika svar, och därför duger inte påstående ett.

(2): Här fås en uppgift om hur många meter tyg som är kvar på rullen, samt några instruktioner om hur stora de sålda bitarna är. Vi vet att när 50% av tyget, och sedan 20% av den kvarvarande biten är sålda, återstår åtta meter. Det går därmed att räkna ut med påstående två.

Svar: B, i (2) men ej i (1).

Hej, varför får man fel svar om man tänker att informationsdel 2 säger att man ska först ta 50% av tyget och då kvarstår 50% av det hela men sedan tar man bort 20% av 50% som vi hade kvar. Alltså 50%-20% =30% , så har vi bara 30% av tyget och det ska vara lika med 8 meter. 3/10* L = 8  , det ger L= ca 26 m. Men det är fel. Svaret ska bli 20 m . 

Det är 1/5 av det som är kvar, inte en femtedel av det som var från början.

I am Me skrev:

Smutstvätt skrev:

NOG:

Ett tyg säljs som metervara från en rulle. Hur många meter tyg finns det på rullen?

(1) Om affären säljer en femtedel av tyget på rullen och därefter en fjärdedel av återstoden av tyget så finns 60 procent av tyget kvar på rullen.

(2) Om affären säljer hälften av tyget på rullen och därefter en femtedel av återstoden av tyget så finns åtta meter tyg kvar på rullen.

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

---

(1): I detta påstående ges information om hur bitarna som säljs förhåller sig till varandra, men inget om hur mycket tyg det finns. Om tyget är en meter långt från början, eller etthundra meter, ger helt olika svar, och därför duger inte påstående ett.

(2): Här fås en uppgift om hur många meter tyg som är kvar på rullen, samt några instruktioner om hur stora de sålda bitarna är. Vi vet att när 50% av tyget, och sedan 20% av den kvarvarande biten är sålda, återstår åtta meter. Det går därmed att räkna ut med påstående två.

Svar: B, i (2) men ej i (1).

Hej, varför får jag fel svar. Informations del 2 säger att först säljer man 50% av tyget och sedan 20% av tyget och det som kvar är lika med 8 meter. Det betyder att 50%-20% = 30% , 30%*L = 8 

Alltså 3/10 * L = 8 och när jag löser ekvationen så får jag L blir ca 26m . Men det är fel. Svaret ska bli 20m. Varför mitt tänkesätt är fel? 

Du har fått svar på ditt första inlägg om den här frågan.

I am Me skrev:

Smutstvätt skrev:

NOG: En klass ska utökas med 12 barn. Kan man därefter dela in klassen i grupper om 8 barn?

(1) Om klassen istället utökades med 4 barn så kan man dela in barnen i grupper om 8 barn.

(2) Innan klassen utökas är det inte möjligt att dela in barnen i grupper om 8 barn.

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

---

(1): Kalla antalet barn för b. Vi vet att $b+4$ är delbart med åtta. Till b adderas tolv, alltså $b+12$. Notera att:

$$\begin{gathered} b+12=b+4+8= \\ (b+4)+8 \end{gathered}$$

b + 4 kunde konstateras vara delbar med 8, och då kvarstår en åtta, som självklart är delbar med åtta. Slutsatsen blir att b + 12 är delbar med 8, och det är alltså möjligt att besvara frågan med påstående (1).

(2): Notera att vi endast behöver hitta två olika fall, ett där det är möjligt att dela in barnen i grupper om åtta, och ett där det inte är möjligt, för att bevisa att (2) inte räcker.

Om det var ett barn i klassen innan, skulle det inte gå att dela in barnen i grupper om åtta, men om det var fyra barn skulle det innebära att klassens storlek (efter utökningen) var 16 barn. 16 är delbart med 2. Alltså har vi hittat två exempel som ger olika slutsatser, och därmed är inte (2) tillräckligt för att svara på frågan.

Svar: A, i (1) men ej i (2).

Hur kunde man veta att det går att lösa uppgiften med informations del1, om man inte tänker på att 12 är 8+4 ??? Tacksam om någon svarar! 

Om man inte tänker på det så är det nog kört.

I am Me skrev:

Smutstvätt skrev:

NOG:

Ett tyg säljs som metervara från en rulle. Hur många meter tyg finns det på rullen?

[...]

(2) Om affären säljer hälften av tyget på rullen och därefter en femtedel av återstoden av tyget så finns åtta meter tyg kvar på rullen.

[---]

---

[...]

(2): Här fås en uppgift om hur många meter tyg som är kvar på rullen, samt några instruktioner om hur stora de sålda bitarna är. Vi vet att när 50% av tyget, och sedan 20% av den kvarvarande biten är sålda, återstår åtta meter. Det går därmed att räkna ut med påstående två.

Svar: B, i (2) men ej i (1).

Hej, varför får man fel svar om man tänker att informationsdel 2 säger att man ska först ta 50% av tyget och då kvarstår 50% av det hela men sedan tar man bort 20% av 50% som vi hade kvar. Alltså 50%-20% =30% , så har vi bara 30% av tyget och det ska vara lika med 8 meter. 3/10* L = 8  , det ger L= ca 26 m. Men det är fel. Svaret ska bli 20 m . 

Det blir fel när du räknar procent såhär:

Alltså 50%-20% =30%

Nu räknar du med att vi tar bort tjugo procent av den ursprungliga mängden tyg. Om vi hade hundra meter tyg, och tar bort femtio procent av de hundra meterna, har vi femtio meter kvar. Om vi nu tar bort tjugo procent av ursprungsmängden tyg, tar vi bort tjugo meter tyg, och då kan vi räkna $50$, men det är inte så uppgifter är formulerad. Istället säljer tygaffären en femtedel av återstoden av tyget, och då måste vi börja med att beräkna vad tjugo procent av den kvarvarande mängden tyg är.

I am Me skrev:

Smutstvätt skrev:

NOG: En klass ska utökas med 12 barn. Kan man därefter dela in klassen i grupper om 8 barn?

(1) Om klassen istället utökades med 4 barn så kan man dela in barnen i grupper om 8 barn.

[...]

---

(1): Kalla antalet barn för b. Vi vet att $b+4$ är delbart med åtta. Till b adderas tolv, alltså $b+12$. Notera att:

$$\begin{gathered} b+12=b+4+8= \\ (b+4)+8 \end{gathered}$$

b + 4 kunde konstateras vara delbar med 8, och då kvarstår en åtta, som självklart är delbar med åtta. Slutsatsen blir att b + 12 är delbar med 8, och det är alltså möjligt att besvara frågan med påstående (1).

[...]

Svar: A, i (1) men ej i (2).

Hur kunde man veta att det går att lösa uppgiften med informations del1, om man inte tänker på att 12 är 8+4 ??? Tacksam om någon svarar! 

Jag vet inte om det finns något bra sätt att lösa uppgiften utan det. Men det går att använda tankesättet till viss del: 

Antalet barn skriver vi som b. I (1) får vi veta att $b+4$ är delbart med åtta. Vi ska dock utöka klassen med tolv barn. Vi behöver därför ta reda på om $b+12$ är delbart med åtta. För bekvämlighetens skull kan vi börja med att räkna bort barnen i $b+4$, eftersom vi redan vet att de går att dela in i grupper om åtta. Kvar är då: 

$(b+12)-(b+4)=b+12-b-4=12-4=8$

Antalet barn som är kvar efter att vi delat in "$b+4$-barnen" i grupper, är då 8. Dessa åtta barn får vara i en egen grupp om åtta, och vi har då delat upp barnen jämnt. Uppgiften går alltså att lösa. :)

Smaragdalena skrev:

I am Me skrev:

Visa föregående citat

Smutstvätt skrev:

NOG: En klass ska utökas med 12 barn. Kan man därefter dela in klassen i grupper om 8 barn?

(1) Om klassen istället utökades med 4 barn så kan man dela in barnen i grupper om 8 barn.

(2) Innan klassen utökas är det inte möjligt att dela in barnen i grupper om 8 barn.

Tillräcklig information för lösningen erhålls
A: i (1) men ej i (2)
B: i (2) men ej i (1)
C: i (1) tillsammans med (2)
D: i (1) och (2) var för sig
E: ej genom de båda påståendena

---

(1): Kalla antalet barn för b. Vi vet att $b+4$ är delbart med åtta. Till b adderas tolv, alltså $b+12$. Notera att:

$$\begin{gathered} b+12=b+4+8= \\ (b+4)+8 \end{gathered}$$

b + 4 kunde konstateras vara delbar med 8, och då kvarstår en åtta, som självklart är delbar med åtta. Slutsatsen blir att b + 12 är delbar med 8, och det är alltså möjligt att besvara frågan med påstående (1).

(2): Notera att vi endast behöver hitta två olika fall, ett där det är möjligt att dela in barnen i grupper om åtta, och ett där det inte är möjligt, för att bevisa att (2) inte räcker.

Om det var ett barn i klassen innan, skulle det inte gå att dela in barnen i grupper om åtta, men om det var fyra barn skulle det innebära att klassens storlek (efter utökningen) var 16 barn. 16 är delbart med 2. Alltså har vi hittat två exempel som ger olika slutsatser, och därmed är inte (2) tillräckligt för att svara på frågan.

Svar: A, i (1) men ej i (2).

Hur kunde man veta att det går att lösa uppgiften med informations del1, om man inte tänker på att 12 är 8+4 ??? Tacksam om någon svarar! 

Om man inte tänker på det så är det nog kört.

Var schyssta mot varandra, er själva och mot andra här i tråden, och läs vad ni skrivit en gång extra innan ni postar era inlägg. Textinlägg kan lätt framstå som bittra, oavsett avsikt, och därför krävs extra noggrant valda formuleringar och mjuka uttryckssätt, särskilt eftersom många här på forumet är barn! Målet är att användaren ska få svar på sina frågor, inget annat. /moderator