Högergränsvärdets definition

Det står inte vad högergränsvärdet är. Om  t ex. f(x)—>8 när x—>1 fr höger så kan m inte väljas =1. Varje omgivning till 8 måste då innehålla alla f(x)-värden för alla x i någon högeromgivning till 1.

Fortsättningsvis: Låt m vara det givna högergränsvärdet och tillämpa definitionen.

Obs gränsvärdet behöver inte vara lika med m här.

Så du kan börja med att kalla gränsvärdet a.

$\left|f\left(x\right)-a\right|<ϵ$, vilket ekvivalent kan skrivas $-ϵ<f\left(x\right)-a<\epsilon$.

Om a = 0 så erhåller vi direkt att att $\left|f\left(x\right)\right|<ϵ$, så den sökta olikheten blir uppfylld om vi väljer m = $ϵ$.

Sedan skulle jag undersöka de två fallen a > 0 och a < 0.

Säg till om du kör fast.

PATENTERAMERA skrev:

Obs gränsvärdet behöver inte vara lika med m här.

Så du kan börja med att kalla gränsvärdet a.

$\left|f\left(x\right)-a\right|<ϵ$, vilket ekvivalent kan skrivas $-ϵ<f\left(x\right)-a<\epsilon$.

Om a = 0 så erhåller vi direkt att att $\left|f\left(x\right)\right|<ϵ$, så den sökta olikheten blir uppfylld om vi väljer m = $ϵ$.

Sedan skulle jag undersöka de två fallen a > 0 och a < 0.

Säg till om du kör fast.

Kunde vi använda 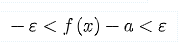För att undersöka när a > 0 och a < 0?

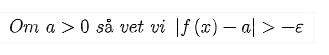Detta kan vara helt fel tankesätt dock
 

Det gäller ju även om a är mindre än noll.

Vi kan skriva om olikheten som

$a-\epsilon <f\left(x\right)<\epsilon +a$. Om a är större än noll så gäller det att $-a-\epsilon <a-\epsilon$.

Så vi har att

$-\left(a+\epsilon \right)<f\left(x\right)<a+\epsilon$.

Kommer du vidare?

PATENTERAMERA skrev:

Det gäller ju även om a är mindre än noll.

Vi kan skriva om olikheten som

$a-\epsilon <f\left(x\right)<\epsilon +a$. Om a är större än noll så gäller det att $-a-\epsilon <a-\epsilon$.

Så vi har att

$-\left(a+\epsilon \right)<f\left(x\right)<a+\epsilon$.

Kommer du vidare?

Om a är mindre än noll är det då:
-a - epsilon > a - epsilon?

För a > 0 fick vi att

$-\left(a+\epsilon \right)<f\left(x\right)<a+\epsilon$,

vilket är ekvivalent med $\left|f\left(x\right)\right|<a+\epsilon$, så i detta fall kan vi välja m = $a+\epsilon$.

Låt nu a vara mindre än noll.

Vi har olikheten

$a-\epsilon <f\left(x\right)<a+\epsilon$.

Då a är mindre än noll så gäller det att $a+\epsilon <\epsilon - a$. Vi får då

$-\left(\epsilon -a\right)<f\left(x\right)<\epsilon -a \iff \left|f\left(x\right)\right|<\epsilon -a$. Så vi kan välja m = $\epsilon -a$.

Notera att vi kan sammanfatta alla fall ovan som att

$\left|f\left(x\right)\right|<\epsilon +\left|a\right|$. Så generellt kan vi välja m = $\epsilon +\left|a\right|$.

Vi kan även härleda detta mha triangelolikheten: $\left|\alpha +\beta \right|\le \left|\alpha \right|+\left|\beta \right|$.

$\left|f\left(x\right)\right|=\left|f\left(x\right)-a+a\right|\le \left|f\left(x\right)-a\right|+\left|a\right|<\epsilon +\left|a\right|$.