Hitta w1 och w2 i bode-diagram

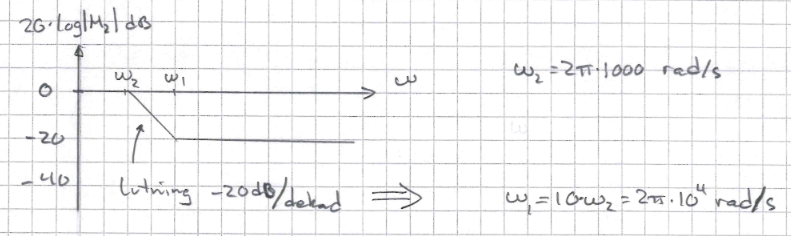
2fly2cry skrev:

jag förstår inte hur lutningen av kurvan kan bestämmas utan att bli given något värde på x-axeln.

Det anges ju att $\omega_1=10\ \omega_2,$ att dessa frekvenser skiljer sig en dekad.

Pieter Kuiper skrev:

2fly2cry skrev:

jag förstår inte hur lutningen av kurvan kan bestämmas utan att bli given något värde på x-axeln.

Det anges ju att $\omega_1=10\ \omega_2,$ att dessa frekvenser skiljer sig en dekad.

I lösningen ja, det anges inte i uppgiften, eller kan man härleda det från 20log|H(w)|? Edit: Glömde kanske att nämna att bilden är från lösningsförslag, inte uppgiften hehe

Hur är uppgiften formulerad? Finns t.ex överföringsfunktionen angiven?

ThomasN skrev:

Hur är uppgiften formulerad? Finns t.ex överföringsfunktionen angiven?

Uppgiften visar att x-axeln är logaritmisk och man förväntas veta att ett sådant filter har en karakteristik med lutning 20 dB per dekad.

Det första att notera att att du just nu har en förenklad skiss av hur amplituden faktiskt kommer se ut.

Du ser att det knycker till vid -20db. Det hade kunnat vara -40db om du hade haft en annan överföringsfunktion. Jag vet inte vad din lärare eller bok har gått igenom, men det är egentligen där det knycker till vi är intresserade. Du kan enkelt räkna hur många decibel linjerna lutar mellan varje knyck genom att kicka på hur mycket den lutar per dekad.  Precis som Pieter är inne på i inlägget ovan.

Dracaena skrev:

Det första att notera att att du just nu har en förenklad skiss av hur amplituden faktiskt kommer se ut.

Du ser att det knycker till vid -20db. Det hade kunnat vara -40db om du hade haft en annan överföringsfunktion. Jag vet inte vad din lärare eller bok har gått igenom, men det är egentligen där det knycker till vi är intresserade. Du kan enkelt räkna hur många decibel linjerna lutar mellan varje knyck genom att kicka på hur mycket den lutar per dekad.  Precis som Pieter är inne på i inlägget ovan.

 

Hmmm, tror att jag hänger med bättre. Verkar som alla filter vi jobbar med har en lutning med 20db/dekad. Tack!

Ett filter som innehåller resistanser samt kapacitanser eller induktanser brukar kallas filter av första ordningen och då är det 20dB/dekad som gäller för amplitud.
Har man resistanser, kapacitanser och induktanser har man filter av andra ordningen och då kan man få 40dB/dekad.

ThomasN skrev:

Ett filter som innehåller resistanser samt kapacitanser eller induktanser brukar kallas filter av första ordningen och då är det 20dB/dekad som gäller för amplitud.
Har man resistanser, kapacitanser och induktanser har man filter av andra ordningen och då kan man få 40dB/dekad.

Tack! Då förstår jag.

Undrar dock vad det är bode-diagrammet visar egentligen? Har förstått det som att det är vilka frekvenser som förstärks, alltså om |H(w)| är positivt under ett intervall på x-axeln så är det dem frekvenserna som förstärks. Men när vi laborerat med filter/ kört simuleringar så blir bode-diagrammet "rundare", är dessa utritade diagram bara approximationer?

Tänk på att ha dB på vertikala axeln och log(w) på horisontella axeln när ni simulerar, så att det går att jämföra med diagrammet i uppgiften.

Om man har passiva komponenter får man ingen förstärkning, det bästa man kan åstadkomma är en dämpning på 0dB.

För att förstå på ett ungefär hur detta filtret fungerar kan man titta på fallen w=0 (likspänning) och w väldigt stor.
För w=0 så har vi samma utspänning som inspänning och för höga w så får vi en spänningsdelning mellan R och R2. Någonstans däremellan sker alltså en förändring i dämpning.

ThomasN skrev:

Tänk på att ha dB på vertikala axeln och log(w) på horisontella axeln när ni simulerar, så att det går att jämföra med diagrammet i uppgiften.

Om man har passiva komponenter får man ingen förstärkning, det bästa man kan åstadkomma är en dämpning på 0dB.

För att förstå på ett ungefär hur detta filtret fungerar kan man titta på fallen w=0 (likspänning) och w väldigt stor.
För w=0 så har vi samma utspänning som inspänning och för höga w så får vi en spänningsdelning mellan R och R2. Någonstans däremellan sker alltså en förändring i dämpning.

Tack!