Hitta rörelseeneergin (A-uppgift)
Fick denna fråga på mitt övningsprov och fattar inte helt och hållet hur man ska göra. Jag vet, efter att ha läst bedömningsanvisningarna att den vertikala komposanten av v0 är 200eV, då 1eV är hur mycket energi det tar att flytta en elektron över 1 volt. Men jag vet inte hur man ska fortsätta.
Såg en tråd om detta, men förstod inte riktigt vad som hände: https://www.pluggakuten.se/trad/bestam-elektrisk-kraft-pa-partikel/#:~:text=Mellan%20tv%C3%A5%20horisontella%20och%20inb%C3%B6rdes,plattan%20f%C3%A5r%20den%20l%C3%A4gsta%20potentialen.
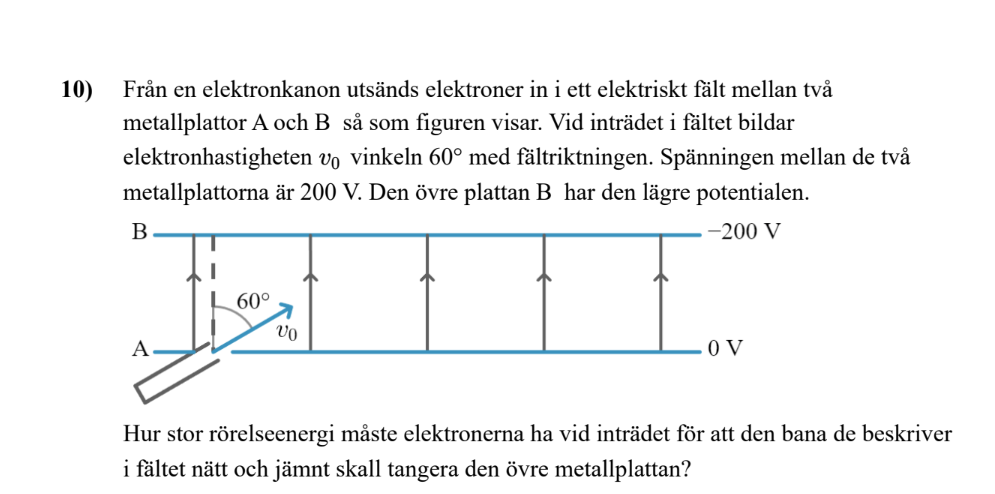
danonduty skrev:Jag vet, efter att ha läst bedömningsanvisningarna att den vertikala komposanten av v0 är 200eV
Då har du nog missuppfattat något. Om v0 är beteckningen av en hastighet kan den inte ha enheten elektronvolt.
Förlåt, rörelseenergin i y-led ska vara 200eV. Men vet fortfarande inte hur man ska göra härifrån.
danonduty skrev:Förlåt, rörelseenergin i y-led ska vara 200eV. Men vet fortfarande inte hur man ska göra härifrån.
Vinkeln är given, så det är bara att bestämma den totala energin.
(Din länk handlar om en annan uppgift, där partikeln är mycket tyngre. Här är det bara en elektron, i den här uppgiften spelar gravitationen ingen roll.)
Skickade fel länk, menade att skicka denna denna: https://www.pluggakuten.se/trad/elektroner-i-homogent-falt/#:~:text=En%20elektronkanon%20s%C3%A4nder%20elektroner%20i,precis%20den%20%C3%B6vre%20metallplattan%20B.
Om man tar cos 60 = Eky/Ek ger det att Ek = 200eV / cos 60 = 400eV, men svaret är att 800eV. Vad är det jag inte tar hänsyn till?
danonduty skrev:Om man tar cos 60 = Eky/Ek
Varför skulle det vara det?
För att det ska vara lättare att begrippa kommer jag skriva det som v istället för v0. Så tanken är att man ska skriva Eky = (mvy^2)/2 = 200eV. Man kan skriva vy som v * cos 60. Därmed får vi att (m(v*cos60)^2)/2 = 200eV. Vi kan separera dessa och skriva de som (mv^2)/2 * cos^2 60 = 200eV. Vi kan skriva om detta som Ek * cos^2 60 = 200eV, och sedan ta Ek= 200eV/cos^2 60 för att få svaret 800eV. Tack för hjälpen.


