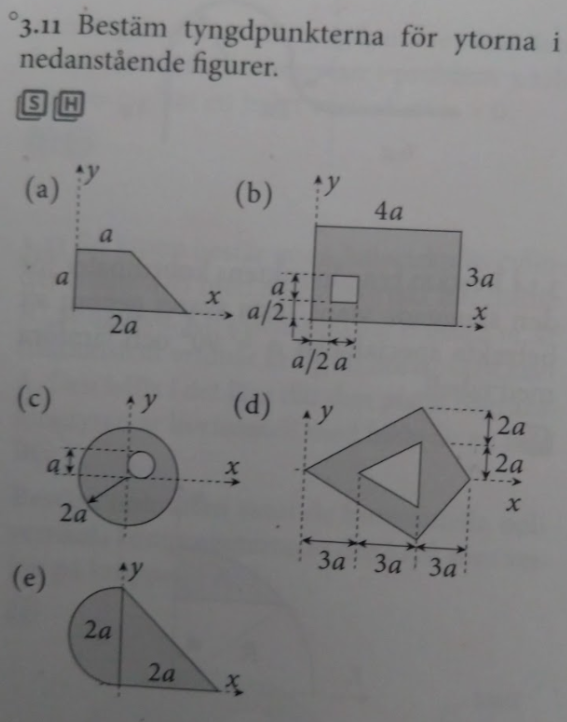
Hitta mittpunkt
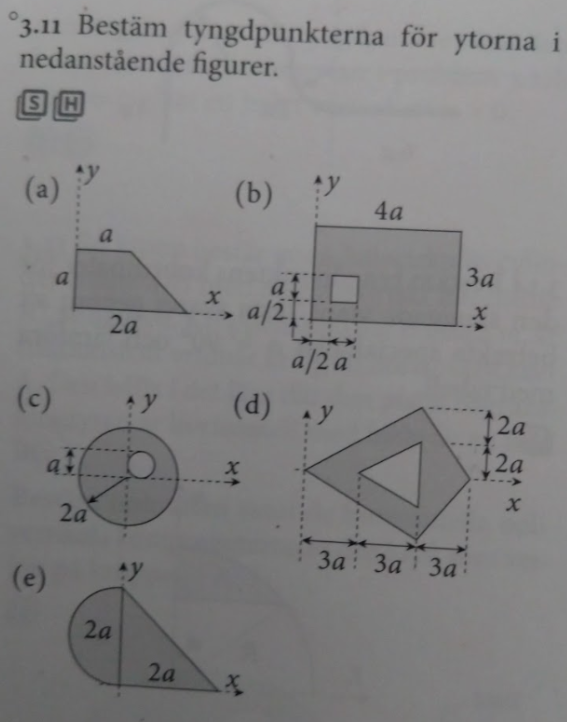
Jag har en liten problem med b
mitt uträkning är
| Figur | Stora kvadrat | Lilla kvadrat |
| Area | ||
| x | 0 | 0 |
| y |
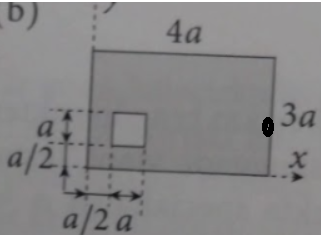
mueoc skrev:
Jag har en liten problem med b
mitt uträkning är
Figur Stora kvadrat Lilla kvadrat Area x 0 0 y Lite information om x och anledning till att jag lagt den till 0.
För att jag har lagt den i x axeln och då gör den alla som finns i dess rad kan man skriva =0
Så här skulle jag tänka: Om det inte hade varit för det lilla kvadratiska hålet, skulle tyngdpunkten ha legat precis i mitten av den stora rektangeln. Nu kan vi tänka oss systemet som en punktmassa i mitten av rektangeln, och en "negativ punktmassa" i mitten av kvadraten. Beräkna tyngdpunkten för detta system.
Jag tycker mig se åtminstone två omedelbara fel med vad du har gjort (å andra sidan hänger jag inte med i dina uträkningar, så jag kan ha missuppfattat något)
1. x-koordinaten kan väl inte vara noll för båda kvadraterna samtidigt, var du än försöker lägga koordinatsystemet?
2. Dimensionsanalys säger mig att koordinater bara kan innehålla faktorn a, aldrig a^2.
(Smaragdalena förslag låter som en bra strategi att minimera antalet beräkningar)
JohanF skrev:Jag tycker mig se åtminstone två omedelbara fel med vad du har gjort (å andra sidan hänger jag inte med i dina uträkningar, så jag kan ha missuppfattat något)
1. x-koordinaten kan väl inte vara noll för båda kvadraterna samtidigt, var du än försöker lägga koordinatsystemet?
2. Dimensionsanalys säger mig att koordinater bara kan innehålla faktorn a, aldrig a^2.
(Smaragdalena förslag låter som en bra strategi att minimera antalet beräkningar)
Ditt punkt 2. Hänger jag inte riktigt med.
mueoc skrev:JohanF skrev:Jag tycker mig se åtminstone två omedelbara fel med vad du har gjort (å andra sidan hänger jag inte med i dina uträkningar, så jag kan ha missuppfattat något)
1. x-koordinaten kan väl inte vara noll för båda kvadraterna samtidigt, var du än försöker lägga koordinatsystemet?
2. Dimensionsanalys säger mig att koordinater bara kan innehålla faktorn a, aldrig a^2.
(Smaragdalena förslag låter som en bra strategi att minimera antalet beräkningar)
Ditt punkt 2. Hänger jag inte riktigt med.
Konstanten a är en längd. Alltså borde areor innehålla faktorn a^2, och koordinater faktorn a
Är du säker på att du skrivit av facits svar på y-koordinaten korrekt? Tittar man i figuren känns det konstigt att den lilla kvadratiska utklippet ska flytta tyngdpunkten i y-led så långt bort från den stora kvadratens tyngdpunkt.
JohanF skrev:Är du säker på att du skrivit av facits svar på y-koordinaten korrekt? Tittar man i figuren känns det konstigt att den lilla kvadratiska utklippet ska flytta tyngdpunkten i y-led så långt bort från den stora kvadratens tyngdpunkt.
17a/11
Tyngdpunkten för den lilla kvadraten (hålet) är och dess area är
Tyngdpunkten för den stora rektangeln är och dess area är .
Arean av hela figuren är
Man beräknar tyngdpunkten genom att "dra bort" hålet i en momentekvation. Så här blir det i y-led:
D4NIEL skrev:Tyngdpunkten för den lilla kvadraten (hålet) är och dess area är
Tyngdpunkten för den stora rektangeln är och dess area är .
Arean av hela figuren är
Man beräknar tyngdpunkten genom att "dra bort" hålet i en momentekvation. Så här blir det i y-led:
Tack för hjälpen.
Sorry att jag inte gav något riktigt svar, bara motfrågor ;-)
Ville få dig att reflektera lite över vad som är realistiska antaganden, slutsatser och svar, och inte. För det mesta kommer man långt enbart med det, dessutom är det då så mycket lättare att själv upptäcka i vilket led man har slarvat eller tänkt fel.
JohanF skrev:Sorry att jag inte gav något riktigt svar, bara motfrågor ;-)
Ville få dig att reflektera lite över vad som är realistiska antaganden, slutsatser och svar, och inte. För det mesta kommer man långt enbart med det, dessutom är det då så mycket lättare att själv upptäcka i vilket led man har slarvat eller tänkt fel.
Ja. jag kan hålla mig dig. Men ibland. Kan man inte hitta felet som man har skapat. För att man inte kan reglerna tillräckligt bra. Detta är det facket som jag ingår i. Men tack ändå.
Var noga med att du förstår hur man hittar tyngdpunkterna för den lilla kvadraten (hålet) och den stora rektangeln. Tyngdpunkterna ligger på symmetrilinjerna i respektive figur. Men det gäller alltså att hitta punkterna i koordinatsystemet också.

D4NIEL skrev:Var noga med att du förstår hur man hittar tyngdpunkterna för den lilla kvadraten (hålet) och den stora rektangeln. Tyngdpunkterna ligger på symmetrilinjerna i respektive figur. Men det gäller alltså att hitta punkterna i koordinatsystemet också.
Det ska jag göra