Hitta maximal synvinkel i biosalong

Hej,

Jag behöver hjälp med en uppgift där jag ska hitta den bästa platsen i en biosalong för att maximera synvinkeln till duken. Uppgiften är från en mattebok och beskriver en biosalong med en duk som är 8 meter hög och börjar 2 meter ovanför golvet. Salongen har en graderingsvinkel på 22 grader för sittplatserna.

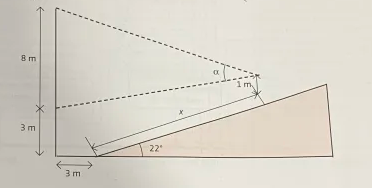
Jag har förstått att jag behöver maximera vinkeln $\alpha$ som visas i figuren, och jag har försökt lösa detta genom att använda derivata. Här är min lösning hittills:

1. Höjden på duken över golvet är totalt 10 meter (8 + 2 meter).

2. Höjden för ögonen är 1 meter över golvet.

Jag har kommit fram till följande uttryck för vinkeln $\alpha$ : $\alpha = \arctan\left(\frac{1}{x}\right) - \arctan\left(\frac{9}{x}\right)$

För att maximera denna vinkel, tog jag derivatan och satte den till noll: $\frac{d\alpha}{dx} = \frac{x^2}{x^2 + 1} - \frac{9x^2}{x^2 + 81}$

Sedan löste jag ekvationen: $\frac{x^2}{x^2 + 1} = \frac{9x^2}{x^2 + 81}$

Detta gav mig att: $x^2 = 9$

Så $x$ är 3 meter från duken. Men jag är osäker på om jag har gjort rätt eller om jag har missat något i min lösning.

Är det någon som kan hjälpa mig att bekräfta min lösning eller ge mig några tips om hur jag kan lösa det på ett annat sätt?

Tack på förhand!

Hej! Bara ett par noteringar, eftersom jag inte räknat själv ännu:

I figuren står att duken börjar 3 m över golvet.
Hur kom du fram till uttrycket för vinkeln a?
Jag ser inte att du använder dig av att golvet lutar 22 grader? Det måste ha betydelse.

sictransit skrev:
Hej! Bara ett par noteringar, eftersom jag inte räknat själv ännu:

I figuren står att duken börjar 3 m över golvet.

Hur kom du fram till uttrycket för vinkeln a?

Jag ser inte att du använder dig av att golvet lutar 22 grader? Det måste ha betydelse.

Tack för att du påpekade det. Jag tänkte att om man sätter sig ner är duken 1m ovanför ögat? Så man subtraherar 1 ifrån 3?
Jag kom fram till uttrycket för vinkeln $\alpha$ genom att räkna ut tangens av vinklarna från ögonhöjden till botten och toppen av duken:

Vi låter z vara vertikala avståndet från tittarens öga till toppen av duken, y vara vertikala avståndet från tittarens öga till botten av duken, och har formeln för synvinkeln enligt följande: $\alpha=\arctan \left(\frac{z}{x}\right)-\arctan \left(\frac{y}{x}\right)$ ; $y=10-1=9$ ; $z=2-1=1$
Du har rätt, jag har inte tagit med lutningen av golvet på 22 grader i min beräkning. Jag inser att detta måste påverka och jag skulle uppskatta hjälp med att förstå hur man inkluderar detta i beräkningen.

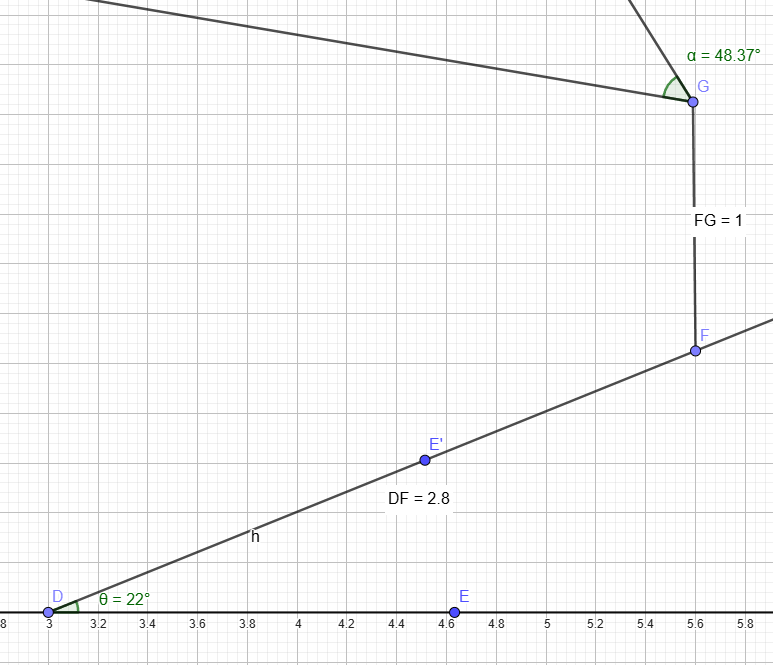
Har inte hunnit räkna ännu, men ritade lite i GeoGebra. Ser vi problemet på samma sätt?

Svara

Visa senaste svar