Hitta eventuella asymptoter
Hej, stötte på dessa två:
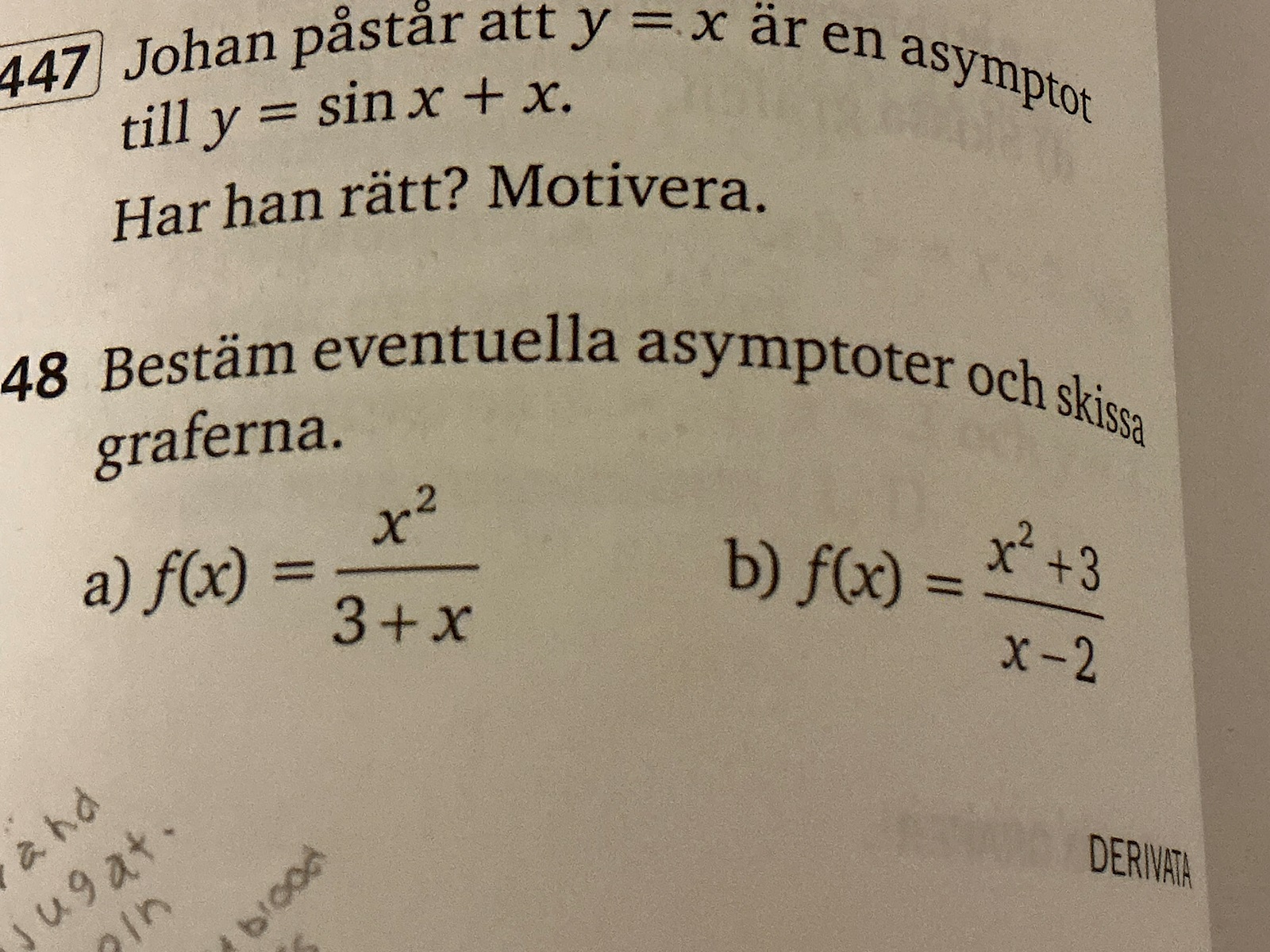
För båda frågorna gjorde jag på följande vis:
a) jag bröt ut x och lät uttrycket gå mot noll. Kvar blev x/1 och alltså fås den sneda asymptoten y =x.
Facit: adderar 9 och subtraherar med nio i täljaren, skriver om bråket så att xˆ2 - 9 /(x+3) och 9/(x+3) skrivs för sig själv. De förkortar den första termen till x-3 och den andra termen går mot noll. Den sneda asymptoten blir y = x-3.
b) jag löste återigen med mitt sätt och fick y= x. Facit: löste på samma sätt som i föregående och fick y= x+2.
Varför fungerar inte mitt sätt varför måste man göra på detta sätt? På vissa uppgifter fungerar min metod. När vet jag vilken metod jag ska använda?
Anonym_15 skrev:[...]
a) jag bröt ut x och lät uttrycket gå mot noll. Kvar blev x/1 och alltså fås den sneda asymptoten y =x.
Om du bryter ut x så blir det f(x)=x·x3+x
Vad menar du med att du "låter uttrycket gå mot noll"?
Facit: adderar 9 och subtraherar med nio i täljaren, skriver om bråket så att xˆ2 - 9 /(x+3) och 9/(x+3) skrivs för sig själv. De förkortar den första termen till x-3 och den andra termen går mot noll. Den sneda asymptoten blir y = x-3.
Det är en stilig lösning. Bra om man kommer på det. Annars kan man köra "brute force", vilket kan vara att först bestämma k i asymptotens ekvation y = kx+m genom att hitta limx→∞f(x)x och sedan bestämma m genom att lösa ekvationen limx→∞(f(x)-(kx+m))=0, dvs bestämma m så att asymptoten går mot grafen då x går mot oändligheten.
b) jag löste återigen med mitt sätt och fick y= x. Facit: löste på samma sätt som i föregående och fick y= x+2.
Varför fungerar inte mitt sätt varför måste man göra på detta sätt? På vissa uppgifter fungerar min metod. När vet jag vilken metod jag ska använda?
Du skriver "bryta ut", men menar du egentligen att du förkortar bråket med x2 i båda fallen?
Så att du i a) får f(x)=13x2+1x och i b) f(x)=1+3x21x-2x2?
I så fall blir det problem då x går mot oändligheten eftersom nämnaren I båda fallen går mot 0.
Den metoden fungerar bra när både täljare och nämnare är av samma grad, dvs då vi letar efter en horisontell asymptot.
Ja, precis jag menar förkorta. alltså fungerar metoden enbart om man ska hitta horisontella asymptoter? Hur vet man om en graf har horisontella eller räta linjer på formen y = kx + m som asymptoter? Och hur menar med att bestämma k? Skulle du kunna ge ett exempel?
Metoden funkar bara om nämnaren har samma eller högre gradtal än täljaren.
=====
En horisontell linje är också en linje på formen y = kx+m, där k = 0.
======
Här är ett exempel på hur den alternativa metoden fungerar. Vi undersöker alltså om det finns en rät linje g(x)=kx+m som är asymptot till f(x).
Vi tar a-uppgiften som exempel, dvs f(x)=x23+x
Om nu gränsvärdet limx→∞f(x)x existerar så är det vårt k-värde.
limx→∞f(x)x=limx→∞xx+3=limx→∞11+3x=1
Vi har alltså att k=1, vilket ger oss g(x)=x+m
Vi söker nu det värde på m som gör att g(x) är en asymptot till f(x), dvs det värde på m som gör att limx→∞(f(x)-g(x))=0.
Ekvationen blir då
limx→∞(x23+x-(x+m))=0
limx→∞(x23+x-(3+x)(x+m)3+x)=0
limx→∞x2-3x-3m-x2-xm3+x=0
limx→∞-3x-3m-xm3+x=0
limx→∞-3-3mx-m3x+1=0
-3-m=0
m=-3
Asymptoten är alltså g(x)=x-3
Pröva gärna samma metod på b-uppgiften, det är bra träning.
Då du beräknar gränsvärdet för f(x) / x, glömmer du inte ett x? Du skriver istället x / (x+3). Titta på sjätte raden av ditt senaste svar.
Nej, men jag hoppade över ett steg.
Eftersom f(x)=x23+x så är f(x)x=x23+xx=x2x·(3+x)= (förkorta med x) =x3+x
(Men jag råkade skriva nämnaren som x+3 istället för 3+x)


