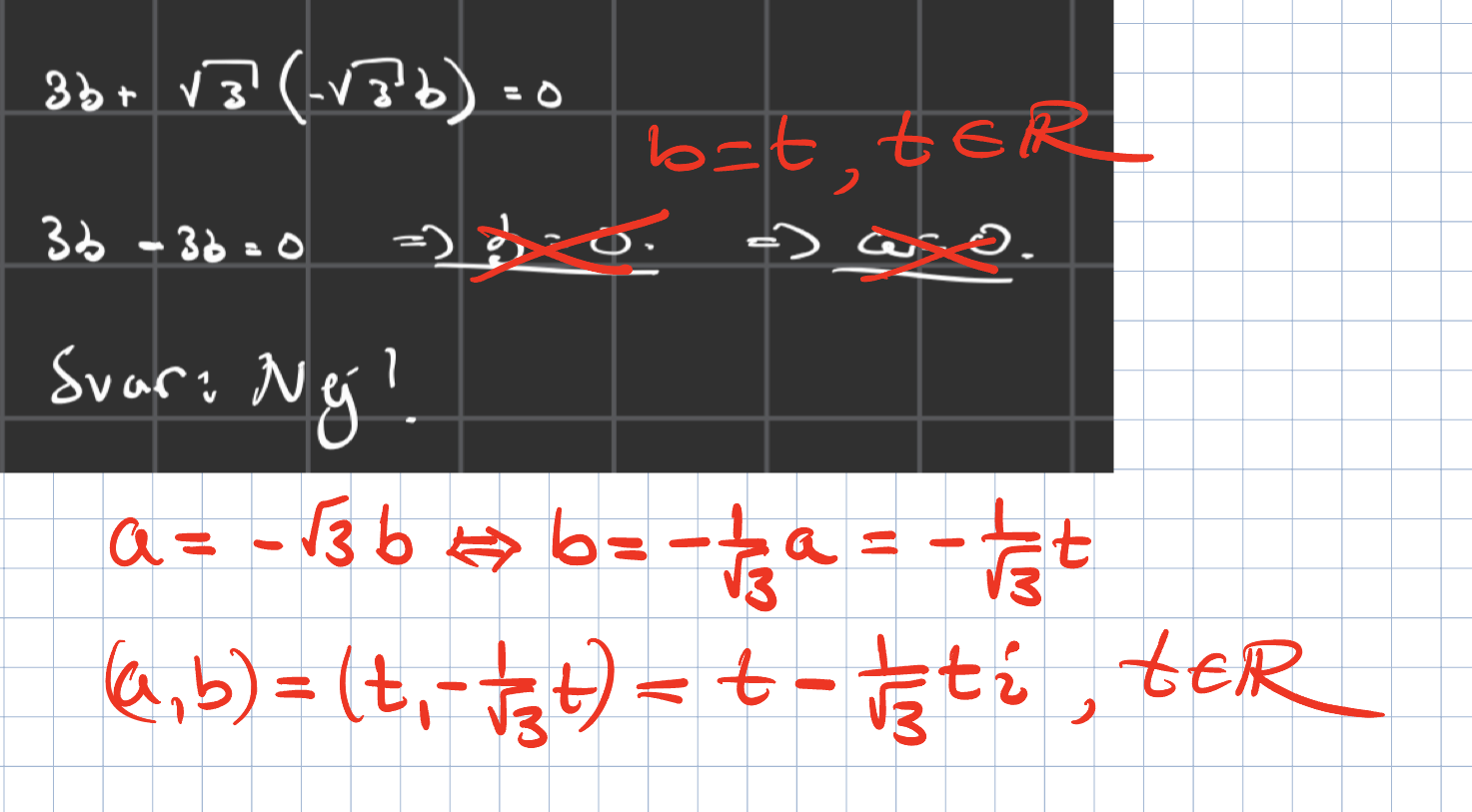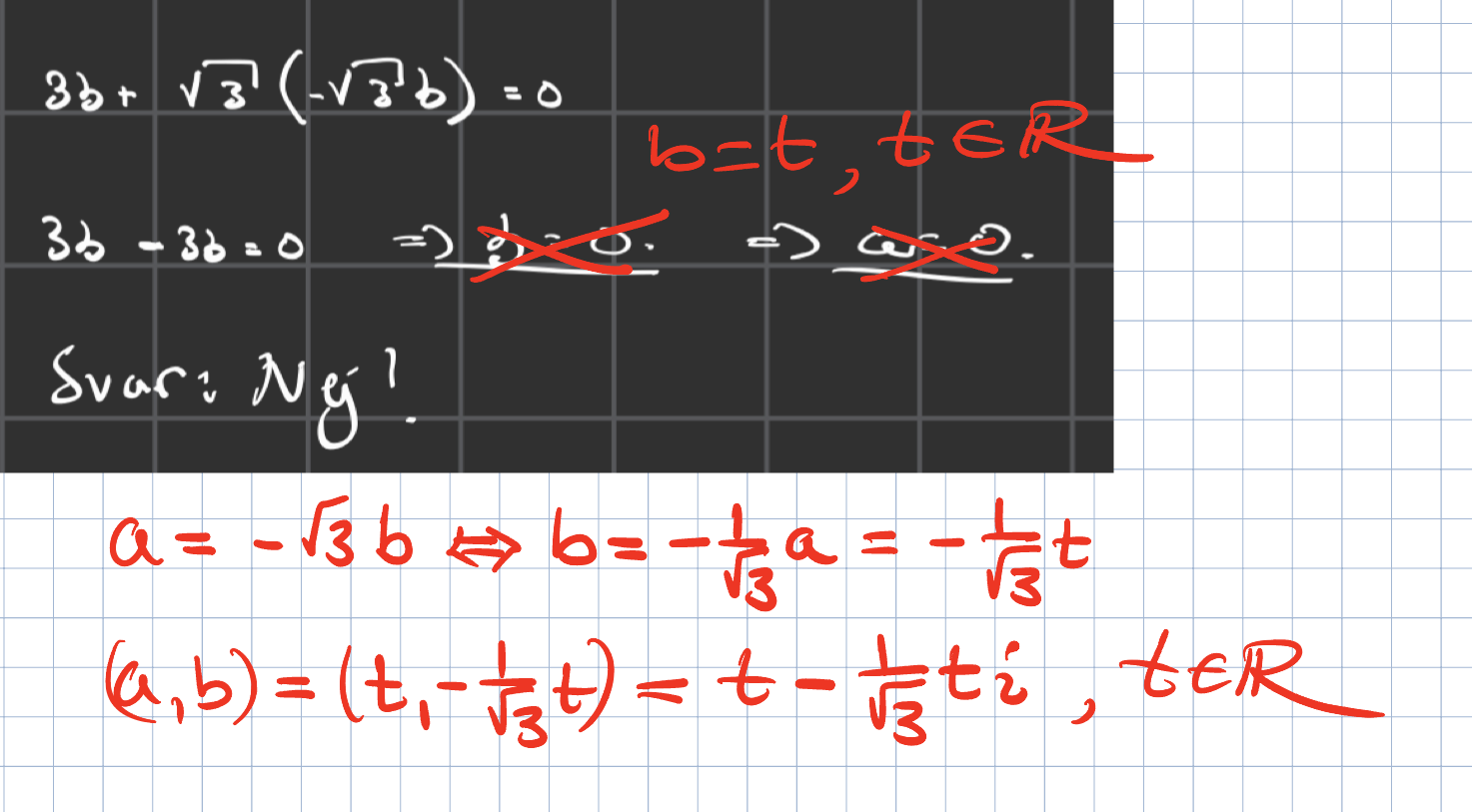Hitta det komplexa talet Z

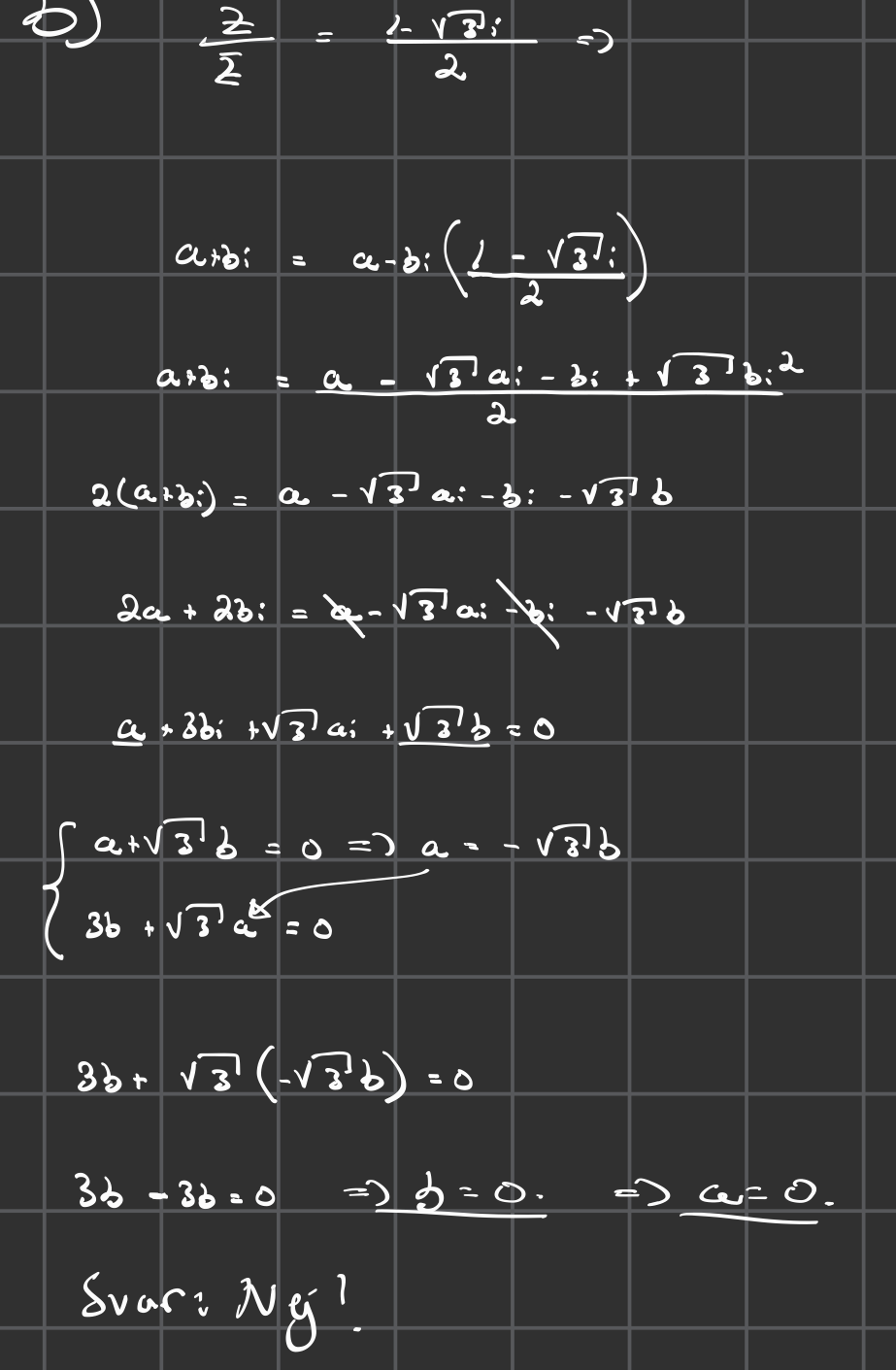
Vad gör du på rad 5 i din uträkning (markerat)?

Jag subtraherar med a i både leden och adderar bi i båda leden

Aha, nu ser jag Vad du gör. Du stryker termer till höger utan att ändra till vänster.

Anonym_15 skrev:

Jag subtraherar med a i både leden och adderar bi i båda leden

OK, men du bör inte separera räkneoperationerna på olika rader på det sättet.

2a - a = a och 2bi + bi = 3bi

Yngve skrev:

Anonym_15 skrev:

Jag subtraherar med a i både leden och adderar bi i båda leden

OK, men du bör inte separera räkneoperationerna på olika rader på det sättet.

nej juste, det ska jag tänka på. 

OK bra. Felet är istället på slutet.

Du kommer fram till att 3b-3b = 0, men betyder det verkligen att b = 0?

Aha, kan det betyda att b kan vara vilket tal som helst eftersom b=b?

Ja, just det. 

Hur går jag sedan tillväga?

Anonym_15 skrev:

Hur går jag sedan tillväga?

Gå över till polära koordinater så blir allt mycket enklare.

Hur ska jag tänka då. r(cos v + isinv) / r(cos v- isinv)?

Anonym_15 skrev:

Hur ska jag tänka då. r(cos v + isinv) / r(cos v- isinv)?

Ansätt 

z=r e^(i theta) 

och allt blir enkelt.

Du kan även räkna vidare från vad du gjort

Trinity2 skrev:

Anonym_15 skrev:

Hur ska jag tänka då. r(cos v + isinv) / r(cos v- isinv)?

Ansätt 

z=r e^(i theta) 

och allt blir enkelt.

Detta är problemet. När vet jag om jag ska ansätta z på polär form, exponentiell form eller rektangulär form?

Trinity2 skrev:

Du kan även räkna vidare från vad du gjort

Hmmm. Ser inte riktigt vad du försöker göra.

Anonym_15 skrev:

Trinity2 skrev:

Du kan även räkna vidare från vad du gjort

Hmmm. Ser inte riktigt vad du försöker göra.

Ekv är sann för alla b, sätt b=t där t är ett reellt tal
beäkna sedan a, som också kommer innehålla t

plotta a och b för lite olika t och du ser vilken graf det blir. Alla tal på denna graf är lösningar

$\frac{z}{\overline{z}}=\frac{z^2}{{\left|z\right|}^2}=e^{-i\pi /3}=e^{i\pi 5/3} dvs z=R{e}^{i\pi 5/6} där R är en godtycklig storlek, och dessutom lösningar för n2\pi$

hansa skrev:

$\frac{z}{\overline{z}}=\frac{z^2}{{\left|z\right|}^2}=e^{-i\pi /3}=e^{i\pi 5/3} dvs z=R{e}^{i\pi 5/6} där R är en godtycklig storlek, och dessutom lösningar för n2\pi$

Enbart i 3e kvadranten?