Hastighetsvektor i polära koordinater
Vi har en positionsvektor som pekar på randen till en cirkel, denna beskrivs enligt
, där r är storleken (längden) av vektorn och är enhetsvektorn som visar riktningen. Vidare beror riktningen på vinkeln som i sig beror av tiden.
Hastighetsvektorn är tidsderivatan av vektorn som är
Min fråga är, varför ens uttrycka en derivata av en skalär då det alltid kommer ge noll?
Bör inte uttrycket för hastigheten vara ?
Både längden och riktningen beror på tiden. En skalär kan vara tidsberoende, liksom en vektor. Vet inte om det hjälper, men annars får du hojta till.
Magnus O skrev:Både längden och riktningen beror på tiden. En skalär kan vara tidsberoende, liksom en vektor. Vet inte om det hjälper, men annars får du hojta till.
Förstår inte hur längden kan bero på tiden. kommer väl alltid peka på randen av cirkeln, så oavsett vart på cirkeln den pekar kommer r förbli konstant?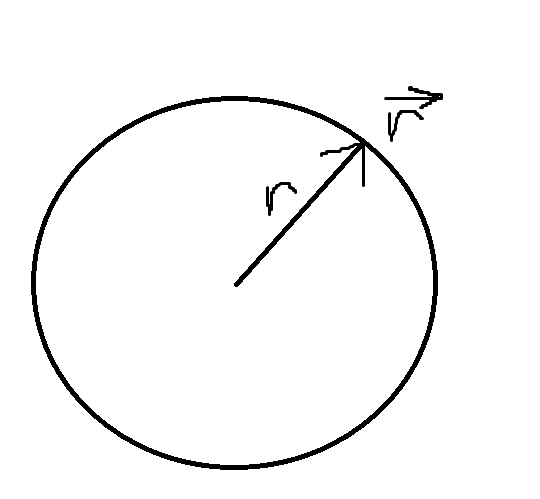
Cirkelns radie kan variera med tiden antar jag. Det framgår kanske i uppgiften?


