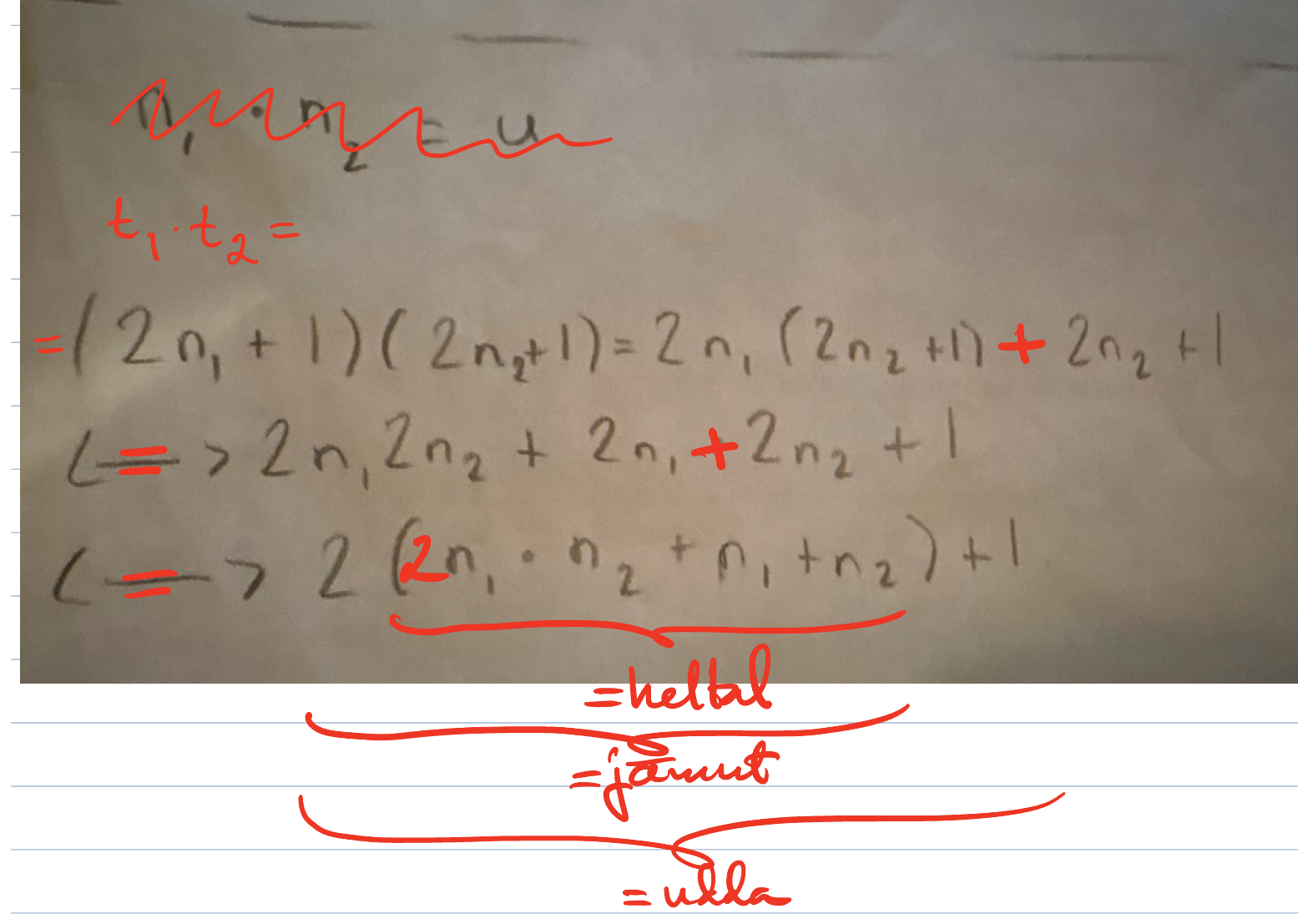Bevis

Detta är mitt bevis, känns dock som att det måste finnas tydligare bevis.

8k^2+1 är visserligen ojämnt. Hur fortsätter jag?

(det är så lockande att skriva om det till 2k^2+1 det är dock ekvivalent så jag borde kunna göra det, eller har jag fel?)

Jag förstår inte riktigt vad som händer mellan den sista och näst sista raden. Det är inte sant i allmänhet att $\displaystyle 4k^2+4k+1 = 8k^2+1$. Men du verkar inte ha berört det allmänna fallet, nämligen då man har två olika (kanske samma) heltal, utan nu håller du på att bevisa specialfallet där du kvadrerar ett udda tal. Börja istället så här:

Låt $n$ och $k$ vara heltal. Då är $z_1 := 2k+1$ och $z_2 := 2n+1$ nödvändigtvis udda heltal. Det följer då att...

Angående 4k^2+4k+1: jag hade blandat ihop ett par andra regler, slarvfel...

Du har rätt, jag antog att udda talen är av samma värde...

naytte skrev:

Jag förstår inte riktigt vad som händer mellan den sista och näst sista raden. Det är inte sant i allmänhet att $\displaystyle 4k^2+4k+1 = 8k^2+1$. Men du verkar inte ha berört det allmänna fallet, nämligen då man har två olika (kanske samma) heltal, utan nu håller du på att bevisa specialfallet där du kvadrerar ett udda tal. Börja istället så här:

Låt $n$ och $k$ vara heltal. Då är $z_1 := 2k+1$ och $z_2 := 2n+1$ nödvändigtvis udda heltal. Det följer då att...

Nu är det rätt! (hoppas det är rätt, annars har jag ingen aning :( )

Trinity2 skrev:

👍 distributiva lagen är ju addition du har rätt, men var parentesen inte korrekt?

Och är det bättre att skriva likhetstecken än ekvivalenstecken? Vad är skillnaden?

edit

Cristian0311

Och är det bättre att skriva likhetstecken än ekvivalenstecken? Vad är skillnaden?

Nu blir jag kanske onödigt teoretisk men jag provar ändå. 

En utsaga kan vara ekvivalent med en annan utsaga. Vad är då en utsaga? Man kanske kan säga att det är något som säger/påstår något, d.v.s. något som kan vara sant eller falskt. Orden utsaga och påstående betyder ungefär samma sak. En likhet är ett exempel på en utsaga. 

Utsagan "2=4" är falsk men utsagan "2x=4" kan vara sann och den är ekvivalent med (den säger samma sak som) utsagan "x=2". (Det betyder att utsagan "2x=4" är sann ifall x=2 annars är den falsk.)

Om vi tittar på din "rad 2" (som inte stämmer, men det bortser vi från nu):

2n₁2n₂+2n₁2n₂+1

så saknar den ett likhetstecken. Det är alltså inget påstående/utsaga och då är den inte ekvivalent med något annat påstående/utsaga heller. Rad 2 är bara ett matematiskt uttryck. Ett uttryck kan vara samma sak som ett annat uttryck och då använder man likhetstecken. 

Det blev väldigt många ord och kanske helt obegripligt men kanske hjälper det lite?

Det hjälper enormt mycket! Har haft problem med att förstå begreppen implikation och ekvivalens. Så i detta scenario skriver jag likhetstecken, men också ekvivalenser där det passar?

tex:

2n2n+2n+2n+1=2(2n^2+n+n)+1

2(2n^2+n+n)+1 <—> 2k+1

(insåg efter att jag lagt upp mitt inlägg att det var fel, alltså att jag räknade distributivalagen fel…)

En ekvivalens mellan två påståenden betyder att båda påståendena medför varandra. Låt oss ställa upp en sanning:

S:= ”Alla rika människor har ett hus”

Låt sedan säga att vi har två påståenden Q:= ”Anna är en rik människa” och P:= ”Anna har ett hus”.

Om P är sant, då måste även Q vara sant enligt vår sanning S (axiom) ovan. Alltså har vi P=>Q. Men vi har samtidigt att om Q är sann, måste P vara sann, alltså har vi dessutom Q=>P. Vi har alltså ekvivalensen P<=>Q, under vår sanning (eller kanske förutsättning är ett bättre ord) S.

Om vi istället hade haft P’ := ”Anna är en rik människa” och Q’ := ”Anna har en bostad” hade vi haft P’=>Q’, men inte Q’=>P’. Alltså har vi implikationen P’=>Q’.

Var det en förståelig förklaring? :)

naytte skrev:

En ekvivalens mellan två påståenden betyder att båda påståendena medför varandra. Låt oss ställa upp en sanning:

S:= ”Alla rika människor har ett hus”

Låt sedan säga att vi har två påståenden Q:= ”Anna är en rik människa” och P:= ”Anna har ett hus”.

Om P är sant, då måste även Q vara sant enligt vår sanning S (axiom) ovan. Alltså har vi P=>Q. Men vi har samtidigt att om Q är sann, måste P vara sann, alltså har vi dessutom Q=>P. Vi har alltså ekvivalensen P<=>Q, under vår sanning (eller kanske förutsättning är ett bättre ord) S.

Om vi istället hade haft P’ := ”Anna är en rik människa” och Q’ := ”Anna har en bostad” hade vi haft P’=>Q’, men inte Q’=>P’. Alltså har vi implikationen P’=>Q’.

Var det en förståelig förklaring? :)

Yes!

Förresten, var min ekvivalens korrekt?:

2(2n^2+n+n)+1 <—> 2k+1

Kan du ge exempel på en ekvation som är ekvivalent respektive implikation?

Kan du ge exempel på en ekvation som är ekvivalent respektive implikation?

Implikation: 

X=1  =>  x²=1

Ekvivalens:

x²=1  <=>  x=±sqrt(1)

Kanske är tydligt? En ekvivalens är, som tecknet antyder, en implikation åt både höger och vänster. 

Peter skrev:

Kan du ge exempel på en ekvation som är ekvivalent respektive implikation?

Implikation: 

X=1  =>  x²=1

Ekvivalens:

x²=1  <=>  x=±sqrt(1)

Kanske är tydligt? En ekvivalens är, som tecknet antyder, en implikation åt både höger och vänster. 

Uppfattat!

Vill tacka er båda, Peter och Naytte, för förklaringarna! 

Insåg precis att det jag menade var ekvivalent, inte ens var ett påstående…