Harmonisk svängningsrörelse

Hej!

Båda metoderna går precis lika bra.. Bra!

Jag får negativt svar i båda. Innebär det att det är en retardation?

Kan man ta reda på om föremålet som hänger i fjädern är på väg upp eller ner om rörelsen är vertikal, eller om föremålet rör sig åt höger eller vänster om det rör sig horisontellt?

Jag tror att föremålet retarderar åt båda hållen.

Jag får negativt svar i båda. Innebär det att det är en retardation?

Kan man ta reda på om föremålet som hänger i fjädern är på väg upp eller ner om rörelsen är vertikal, eller om föremålet rör sig åt höger eller vänster om det rör sig horisontellt?

Jag tror att föremålet retarderar åt båda hållen.

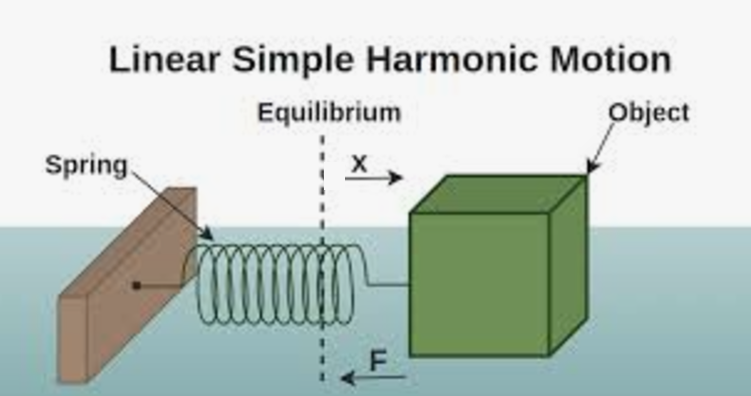
Det är jättebra frågor båda två. Och att du ställer dem visar att du har insett att svaret kanske inte är helt självklart. (Jag ser också nu då jag läser din uträkning noggrannare, att du "trollade" med ett minustecken för att svaren skulle bli lika, eller hur?) För att se vad som egentligen händer så är det bra med en figur. Jag klippte in en nedan.

Att man får en negativ acceleration betyder inte nödvändigtvis att någonting retarderar (dvs saktar ner). En negativ acceleration betyder bara att riktningen på accelerationen är motriktad den koordinataxel du använder för att beskriva läget. Titta på figuren nedan. I ditt fall så är läget +5cm från jämviktsläget (dvs höger om jämviktsläget), så det betyder att accelerationen är riktad åt vänster, tillbaka mot jämviktsläget. Och omvänt, om elongationen hade varit -5cm från jämviktsläget (dvs vänster om jämviktsläget) så hade accelerationen blivit positiv dvs riktad åt höger.

Din första uträkning så borde du ha, för att redovisa helt korrekt med tecken, ha ställt upp:

$$\begin{gathered} ma=-kl \\ a=-\frac{k}{m}·l \end{gathered}$$

så att accelerationen alltid får motsatt tecken mot elongationen, dvs om elongationen är positiv (positivt l, höger om jämviktsläget) så blir accelerationen negativ, riktad tillbaka mot jämviktsläget.

Dock tror jag ingen lärare skulle anmärka på den uträkningen eftersom uppgiften inte efterfrågade riktningen på accelerationen. Man kan lika gärna, som du gjorde, utesluta minustecknet men kanske beskriva att accelerationen är "xxx riktad mot jämviktsläget"

I din alternativa uträkning så antog du att rörelsen beskrevs av $l=A\sin \left(\omega t\right)$, där $l$ är avvikelsen (positiv eller negativ) från jämviktsläget, och man får automatiskt ett $a$ som har motsatt tecken mot $l$

Accelerationen efter deriveringar blir

$a=-{\omega }^{2}A\sin \left(\omega t\right)=-{\omega }^2·l$

men eftersom $\omega =\sqrt{\frac{k}{m}}$ så blir 

$a=-{\omega }^2·l=-\frac{k}{m}·l$

och vi är tillbaka till det samband som du använde i din första uträkning. Med andra ord var det Inte konstigt att det blev samma resultat i dina båda uträkningar.

(Däremot tror jag att du slog nåt fel på miniräknaren där, då du fick en tid på 9.5 sekunder. Har du någon förklaring till det?).

Men iallafall, tillbaka till dina frågor. Retardation blir det bara om accelerationen är motriktad hastigheten, vilket är fallet när föremålet är påväg mot ändläget. Om föremålet är påväg från jämviktsläget (vid samma elongation) så är accelerationen lika stor, med samma tecken, men föremålet retarderar inte utan accelererar, eftersom hastigheten har samma riktning som accelerationen.

Som du ser blir det olika svar på din retardationsfråga beroende på om föremålet rör sig mot ändläget eller mot jämviktsläget. På det sätt som frågan är ställd så kan man inte veta vilket som är fallet, eftersom texten bara specificarar läget, men inte hastigheten.

Jag svävade ut lite, och inte riktigt säker på om jag svarade på det du frågade efter. Men isåfall fråga igen! 

För att räkna ut tiden när elongationen y=0,05m använder jag

y=Asin(wt).

0,05=0,1sin(pi*t)

t=(arcsin(0,05/0,1))/(pi)=~ 9,55 sekunder. Gör jag någt fel här?

Tack för bilden och förklaringen!

Om du kontrollerar din uträkning genom att stoppa in tiden i formeln, så får du:

$0.1·\sin (\pi ·9,55)\ne 0,05$

så nånstans är det fel.

Om jag slår

$t=\frac{arc\sin \left({\displaystyle \frac{0.05}{0.1}}\right)}{\pi }$ på miniräknaren, så får jag

$t=0.167+n·2$

periodiciteten 2 kommer sig av att föremålet kommer tillbaka till samma läge efter svängningsperiodtiden. Det finns ju en andra lösning på ekvationen också

$t=0.833+n·2$

vilken är de tidpunkter som föremålet har samma elongation, men färdas mot jämviktsläget istället för från jämviktsläget.

Men ingen av dessa tidpunkter överensstämmer med 9.55 sekunder som du räknade ut.

Oj, det stämmer. Jag hade ställt in min grafräknare på grader. Nu när jag räknar på radianer så får jag också att t=0,167s. 
a=-w^2*A= -pi*0,1*sin(0,167*pi)= -0,494m/s^2

Får ändå samma svar i slutändan.

Ja, det var därför jag inte uppmärksammade felet först, då du ändå fick rätt svar i slutändan. (Helt enkelt eftersom räkneoperationerna var arcsin följt av sin, så blev det rätt ändå, men fel påvägen 😊).

Det är ju jättelätt att ha fel vinkelenhet inställd på räknaren, men i det här fallet kan man reflektera om resultatet är rimligt. Låter det vettigt att få en tid på över 9 sekunder för föremålet att nå halvvägs, om periodtiden på svängningen är 2 sekunder? (Nu är det glömt 😊)

Jag förstår. Det låter absolut inte rimligt. Tack så jättemycket för hjälpen! 

 👍