Härled formeln för en cylinders volym

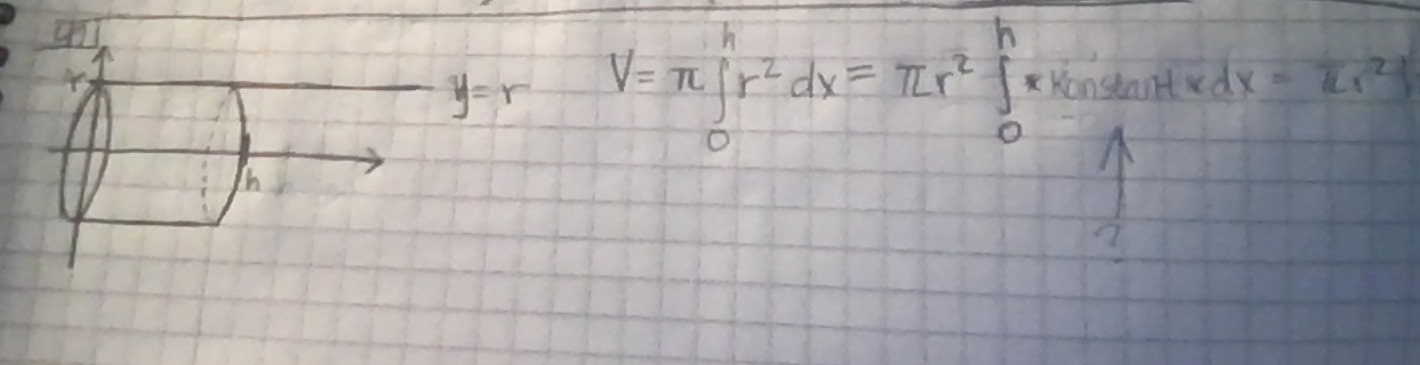
edit: här gick det litet fort, jag kollade bara på din lösning och inte på uppgiften. Du skall integrera på andra ledden, se nästa post.

Approach och resultat rätt. Noteringen om konstant h gör lösning lite otydlig tycker jag. 
Räcker med ”integralsymbol från 0 till h” dx efter att du brutit ut pi och r2.

Analys skrev:

Approach och resultat rätt. Noteringen om konstant h gör lösning lite otydlig tycker jag. 
Räcker med ”integralsymbol från 0 till h” dx efter att du brutit ut pi och r2.

Du skall, enligt uppgiften, betrakta cylindern som ett oändligt antal tunna skal, typ konservburkar  inuti varandra. Varje skal har ytan=h*omkrets = h*2pi*r och tjockleken dr.

Analys skrev:

edit: här gick det litet fort, jag kollade bara på din lösning och inte på uppgiften. Du skall integrera på andra ledden, se nästa post.

Approach och resultat rätt. Noteringen om konstant h gör lösning lite otydlig tycker jag. 
Räcker med ”integralsymbol från 0 till h” dx efter att du brutit ut pi och r2.

Stämmer alltså detta nedan? Visste inte att man kunde använda integralsymbolen utan integrand 😮

${\int }_0^{h}dx=h$

Du skall, enligt uppgiften, betrakta cylindern som ett oändligt antal tunna skal, typ konservburkar  inuti varandra. Varje skal har ytan=h*omkrets = h*2pi*r och tjockleken dr.

Hmm, förstår inte varför jag inte kan tänka att jag har en rak linje y=r som roterar kring x-axeln, och sedan räkna ut rotationsvolymen mha formeln i formelbladet?

Majskornet skrev:

Analys skrev:

edit: här gick det litet fort, jag kollade bara på din lösning och inte på uppgiften. Du skall integrera på andra ledden, se nästa post.

Approach och resultat rätt. Noteringen om konstant h gör lösning lite otydlig tycker jag. 
Räcker med ”integralsymbol från 0 till h” dx efter att du brutit ut pi och r2.

Stämmer alltså detta nedan? Visste inte att man kunde använda integralsymbolen utan integrand 😮

${\int }_0^{h}dx=h$

Jodå, du kan tänka dig att det står en ”1”:a, det är ju faktuskt talet 1 som är integrand. Eller låt r2 stå kvar.

Majskornet skrev:

Du skall, enligt uppgiften, betrakta cylindern som ett oändligt antal tunna skal, typ konservburkar  inuti varandra. Varje skal har ytan=h*omkrets = h*2pi*r och tjockleken dr.

Hmm, förstår inte varför jag inte kan tänka att jag har en rak linje y=r som roterar kring x-axeln, och sedan räkna ut rotationsvolymen mha formeln i formelbladet?

Om denna raka linje roterar runt x-axeln ett varv så har den ju byggt upp ett skal eller ett tunt rör om du föredrar det. Sen gäller det att integrera över alla r. Vad står deti formelbladet?

Aha, förstår vad du menar. Vi har lärt oss en formel för hur man direkt räknar ut volymen, samma som jag skrev upp i min lösning, så jag tror att det blir rätt så.