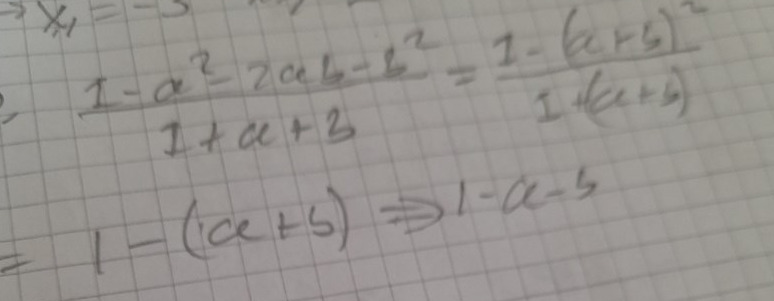Hårig Uttryck

Jag gjorde så här:

Skulle ni också löst på samma sätt ?

Arup skrev:

Jag gjorde så här:

Första raden skulle jag ha gjort likadant. Sedan skulle jag ha använt konjugatregeln baklänges på täljaren, så att jag kan förkorta. Din andra rad hänger jag inte med på.

kan du visa hur du menar med "konjugat regeln baklänges" ?

a²-b² =(a+b)(a-b), i det här fallet är a = 1 och b = (a+b).

Vad menar du med att uttrycket är "hårigt"?

jobbigt

"Håriga uttryck" eller "håriga uträkningar" kan jag också säga.

Ett bra sätt att förenkla uttryck är ofta att ersätta återkommande komplicerade uttryck med andra enklare. Då framträder struktur tydligare och det blir lättare att se vad som ska göras härnäst. Efter förenklingar kan man byta tillbaka från det enklare uttrycket till det mer komplicerade.

I det här fallet (vi kallar uttrycket $U$):

$U=\frac{1-a^2-2ab-b^2}{1+a+b}=\frac{1-(a^2+2ab+b^2)}{1+a+b}$

Första kvadreringsregeln i täljaren och parenteser i nämnaren ger

$U=\frac{1-(a+b)^2}{1+(a+b)}$

Vi ser att uttrycket $a+b$ förekommer på flera ställen och för att underlätta fortsättningen så ersätter (substituerar) vi nu tillfälligt $(a+b)$ med $c$:

$U=\frac{1-c^2}{1+c}$

Nu träder mönstret $x^2-y^2$ tydligare fram, vilket leder oss till att använda konjugatregeln i täljaren:

$U=\frac{(1+c)(1-c)}{1+c}$

Vi ser att uttrycket är odefinierat då $c=-1$.

För alla andra värden på $c$ kan vi förkorta med $1+c$ och vi får då:

$U=1-c$

Nu har vi förenklat så långt det går och vi byter då tillbaka från $c$ till $a+b$.

Vi får då

$U=1-(a+b)=1-a-b$

Förenklingen gäller för alla $a$ och $b$ förutom de som uppfyller $a+b=-1$.

Laguna skrev:

"Håriga uttryck" eller "håriga uträkningar" kan jag också säga.

Jag fick rätt svar enligt facit

Arup skrev:

Jag fick rätt svar enligt facit

Bra. Men du bör även skriva att förenklingen endast gäller då $a+b\neq-1$

Man kan prova polynomdivision också. Vi betraktar a som variabel och behandlar allt annat som konstanter:

a+b+1 går -a-2b gånger i 1-a²-2ab-b² (för att a går -a-2b gånger i det).

Produkten är (-a-2b)(a+b+1) = -a²-ab-a-2ab-2b²-2b = -a²-3ab-a-2b²-2b. Resten är 1+ab+b²+2b.

a+b+1 går b gånger i 1+ab+b²+2b. b(a+b+1) = ab+b²+b. Resten är 1+b.

Nu gjorde jag tydligen fel. Hittar du felet?

Polynomdividion dyker inte föränn Matte 4