26 svar

217 visningar

Halvsfär upphängd i ett snöre, lutandes mot en vägg

Jag har några frågor om följande uppgift. Till a, är detta en trickfråga? jag tänker i alla fall att phi är 45 grader då vi har en liksidig triangel.

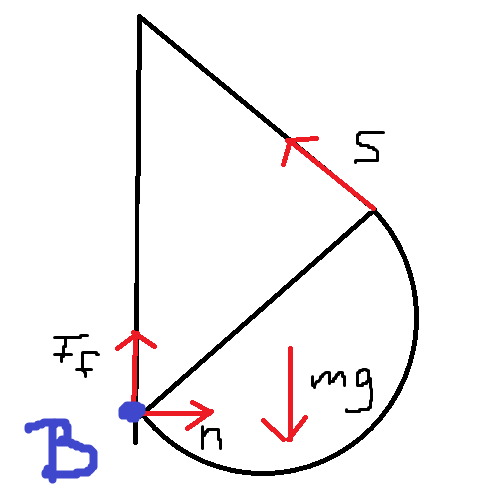
Till uppgift b så tänker jag att vi kan använda oss utav kraftmoment för att beräkna snörkraften. Jag lägger vridningsaxeln i punkt B (bild nedan). Här hamnar jag dock i lite trubbel, jag måste veta det rätvinkliga avståndet från väggen till mg. I texten säger de att tyngdpunkten ligger på avståndet 3r/8 av en halvsfär, vet inte riktigt hur jag ska tyda det. Men om avståndet till mg är d så kan vi väl beräkna kraftmomentet som mgd-S*2r=0?

Det är en likbent triangel. Om det varit en liksidig triangel så skulle $φ = 60^{°}$ .

Jag undrar vad "söder mot väggen" betyder.

Jag hittar inget verb "att söda" i SAOL.

PATENTERAMERA skrev:
Det är en likbent triangel. Om det varit en liksidig triangel så skulle $φ = 60^{°}$ .

Ok så phi beror egentligen på hur långt avståndet är från A till B?

Pieter Kuiper skrev:
Jag undrar vad "söder mot väggen" betyder.

Jag hittar inget verb "att söda" i SAOL.

Inte säker jag förstår vad du menar.

Cien skrev:
Inte säker jag förstår vad du menar.

Vad betyder detta?
Ska kanske vara "stöder"?

Pieter Kuiper skrev:
Cien skrev:
Inte säker jag förstår vad du menar.

Vad betyder detta?
Ska kanske vara "stöder"?

Det var konstigt. Jag antar att det ska stå stöder ja.

Cien skrev:
PATENTERAMERA skrev:
Det är en likbent triangel. Om det varit en liksidig triangel så skulle $φ = 60^{°}$ .

Ok så phi beror egentligen på hur långt avståndet är från A till B?

Ja, om B är sfärens stödpunkt mot väggen.

PATENTERAMERA skrev:
Cien skrev:
PATENTERAMERA skrev:
Det är en likbent triangel. Om det varit en liksidig triangel så skulle $φ = 60^{°}$ .

Ok så phi beror egentligen på hur långt avståndet är från A till B?

Ja, om B är sfärens stödpunkt mot väggen.

Jag tänker att man kan använda cosinussatsen för att beräkna phi men då beror phi på längden AB som är okänd. Låter det rimligt?

Du ska hitta vinkeln där kraften parallellt med väggen är noll.

Cien skrev:
PATENTERAMERA skrev:
Cien skrev:
PATENTERAMERA skrev:
Det är en likbent triangel. Om det varit en liksidig triangel så skulle $φ = 60^{°}$ .

Ok så phi beror egentligen på hur långt avståndet är från A till B?

Ja, om B är sfärens stödpunkt mot väggen.

Jag tänker att man kan använda cosinussatsen för att beräkna phi men då beror phi på längden AB som är okänd. Låter det rimligt?

Du får ställa upp jämviktsekvationer och bestämma den vinkel vid vilken jämvikt är möjlig.

Alternativt kan du försöka hitta den vinkel som minimerar den potentiella energin, dvs den vinkel som gör att tyngdpunkten hamnar så långt ner som möjligt.

PATENTERAMERA skrev:
Cien skrev:
PATENTERAMERA skrev:
Cien skrev:
PATENTERAMERA skrev:
Det är en likbent triangel. Om det varit en liksidig triangel så skulle $φ = 60^{°}$ .

Ok så phi beror egentligen på hur långt avståndet är från A till B?

Ja, om B är sfärens stödpunkt mot väggen.

Jag tänker att man kan använda cosinussatsen för att beräkna phi men då beror phi på längden AB som är okänd. Låter det rimligt?

Du får ställa upp jämviktsekvationer och bestämma den vinkel vid vilken jämvikt är möjlig.

Alternativt kan du försöka hitta den vinkel som minimerar den potentiella energin, dvs den vinkel som gör att tyngdpunkten hamnar så långt ner som möjligt.

När jag ställer upp jämviktsekvation för kraftmomentet, ska jag ställa upp summan av krafterna som är parallella med väggen då?

Jag förväxlar detta lite med liknande uppgifter där vi har en stege som lutar mot en vägg. När vi till stegen tar fram kraftmomentet så tar man alla kraftkomponenter ortogonala mot stegen.

I denna uppgift, likt stegen, så har vi en en rät linje som lutar snett, men ska krafterna till jämviktsekvationen för kraftmoment vara ortogonala mot denna linje också? eller ska krafterna vara parallella med väggen?

Du har tre obekanta: vinkeln fi, normalkraften och snörkraften. Du behöver sätta upp tre jämviktsekvationer - två kraftekvationer och en momentekvation. Notera att vinkeln vid A också är fi pga likbent triangel.

Det är kanske enklast att komposantuppdela krafterna i vertikal och horisontalled med tanke på riktningarna på normal- och tyngdkraft.

Sedan får du välja lämplig momentpunkt.

PATENTERAMERA skrev:
Du har tre obekanta: vinkeln fi, normalkraften och snörkraften. Du behöver sätta upp tre jämviktsekvationer - två kraftekvationer och en momentekvation. Notera att vinkeln vid A också är fi pga likbent triangel.

Det är kanske enklast att komposantuppdela krafterna i vertikal och horisontalled med tanke på riktningarna på normal- och tyngdkraft.

Sedan får du välja lämplig momentpunkt.

Jag kallar snörkraften T. d är avståndet från väggen till mg.
$\Sigma F_x=n-Tsin \phi=0$

$\Sigma F_y=F_f+Tcos\phi-mg=0$

$\Sigma \tau_B = dmg-2rTcos \phi =0$

Som sagt lite osäker på 3de ekvationen då jag inte vet om krafterna ska vara parallella med väggen eller ej.

Edit: Skulle jag inte ha med friktion?

Väggen är glatt, dvs ingen friktion.

PATENTERAMERA skrev:
Väggen är glatt, dvs ingen friktion.

Det visste jag inte, grymt då vet jag :) återkommer

PATENTERAMERA skrev:
Väggen är glatt, dvs ingen friktion.

$\Sigma F_x=n-Tsin \phi=0$

$\Sigma F_y=Tcos\phi-mg=0$

$\Sigma \tau_B = dmg-2rTcos \phi =0$

Vet inte riktigt hur jag ska lösa ekvationssystemet. 3 ekvationer, 4 obekanta (n,T, $\phi$ , d). Jag skrev tredje ekvationen lite nonchalant, tror problemet ligger här.

Edit: Jag har förväxlat $\varphi$ med $\phi$ , låt oss vidare fortsätta med $\phi$

Edit2: Från din tidigare post skrev du att vi har 3 obekanta, hur tänkte du då?

Jag tänker något sånt här för att hitta center of mass. Men jag vill väl ha den nedre kateten till den "nya triangeln" att vara ortogonal med väggen eller?

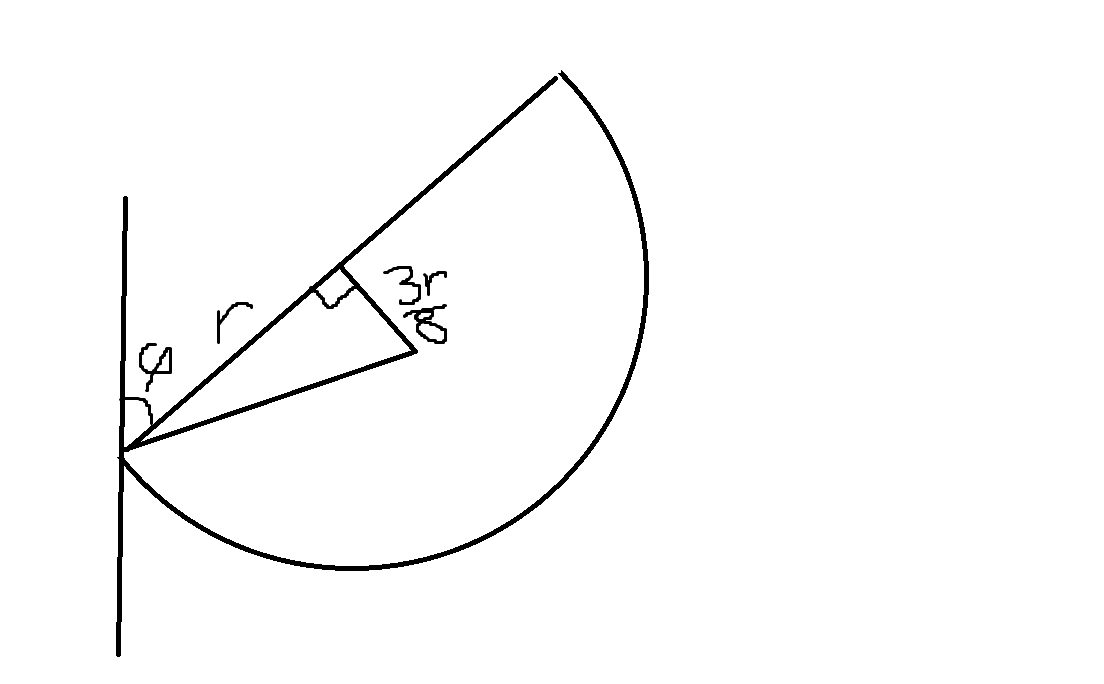
Tänk på att när man beräknar moment så använder man bra den komposant av kraften som är vinkelrät mot hävarmen.

Man kan dock med fördel använda kryssprodukten för att beräkna momentet.

${\vec{τ}}_{B} = \vec{B C} \times \vec{S}$ . Om ni gått igenom det så kan du utnyttja det i detta problem.

PATENTERAMERA skrev:
Tänk på att när man beräknar moment så använder man bra den komposant av kraften som är vinkelrät mot hävarmen.

Man kan dock med fördel använda kryssprodukten för att beräkna momentet.

${\vec{τ}}_{B} = \vec{B C} \times \vec{S}$ . Om ni gått igenom det så kan du utnyttja det i detta problem.

Vi har gått igenom det lite, känner mig inte bekväm med den dock :(

Så vi ska alltså vara vinkelrät mot den räta linjen. Det är ju S som jag bytt till T nu som är vinkelrät mot hävarmen? Den vinkelrätta komposanten av mg blir då mgsin $\phi$ . Men som sagt jag saknar avstånden till kraftmomenten. Vet inte hur jag ska beräkna detta avstånd d.
$\Sigma \tau_B=dmgsin\phi-2rT=0$

T är inte nödvändigtvis vinkelrät mot hävarmen.

PATENTERAMERA skrev:
T är inte nödvändigtvis vinkelrät mot hävarmen.

För att förtydliga, är röd hävarmen?

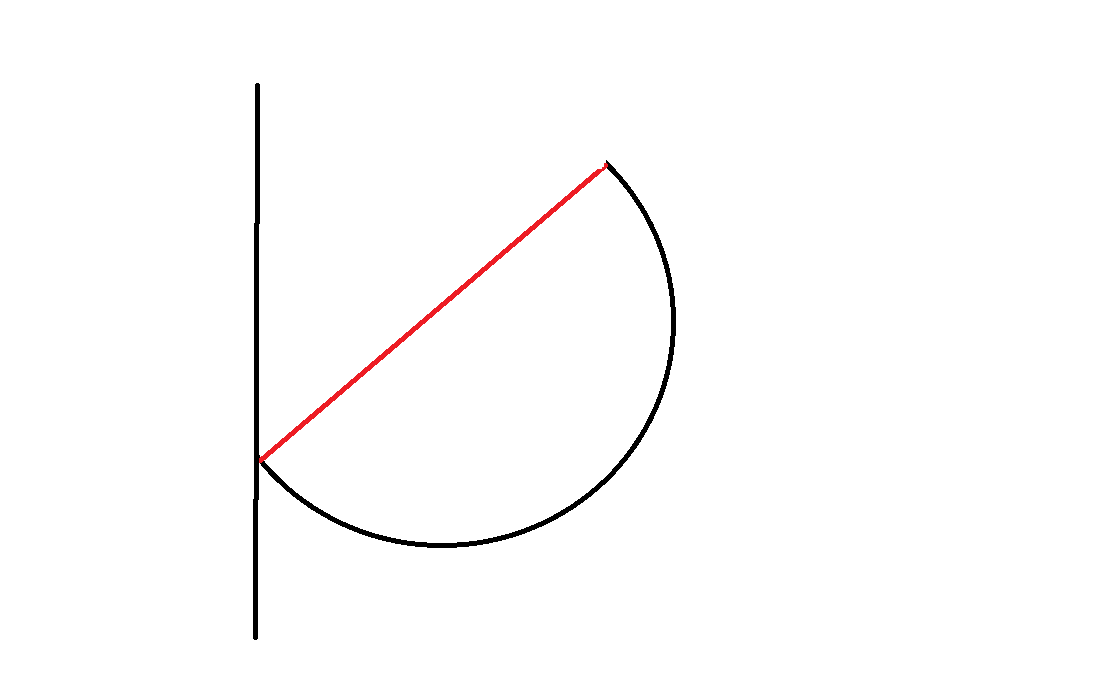
PATENTERAMERA skrev:
T är inte nödvändigtvis vinkelrät mot hävarmen.

Tror jag förstår nu, $Tcos\phi$ är vinkelrät mot hävarmen?

Jag tar tillbaka det. Ingen aning hur jag hittar komponenten till T som är vinkelrät mot hävarmen.

Jan Ragnar skrev:

Tack ska du ha för den fina bilden! jag ska gå igenom detta mer i detalj

Svara

Visa senaste svar