Halvledare - PN övergång

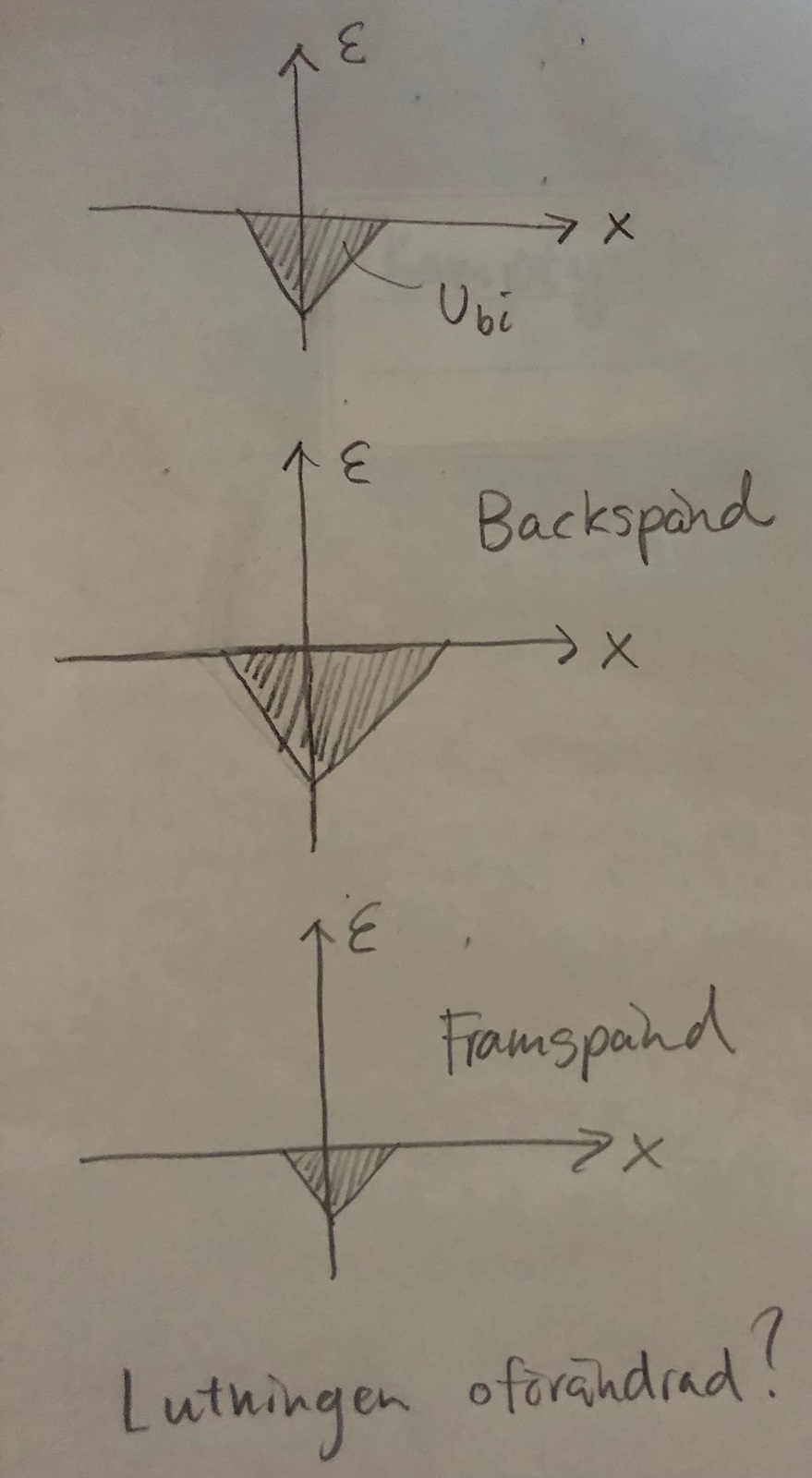
Jag har här skissat det elektriska fältet för en PN övergång och hur det förändras med back-/framspänning.

Jag är lite osäker på vad som egentligen händer med lutningen på E-fältet då en spänning läggs på. Utarmningsområdet ändras, det vet jag. Sen tänker jag att triangelns storlek ändras så att den fortfarande är likformig med det icke-biaserade fallet. Lutningen är väl bara proportionell mot dopkoncentrationen, eller? E_max (dvs triangelns topp) ökar ju i höjd lika mycket som dp (och dn) ökar i sidled.

Alltså förändras inte lutningen med pålagd spänning.

Har jag fel? En lärare gav mig feedback som fick mig att tvivla på mitt resonemang.

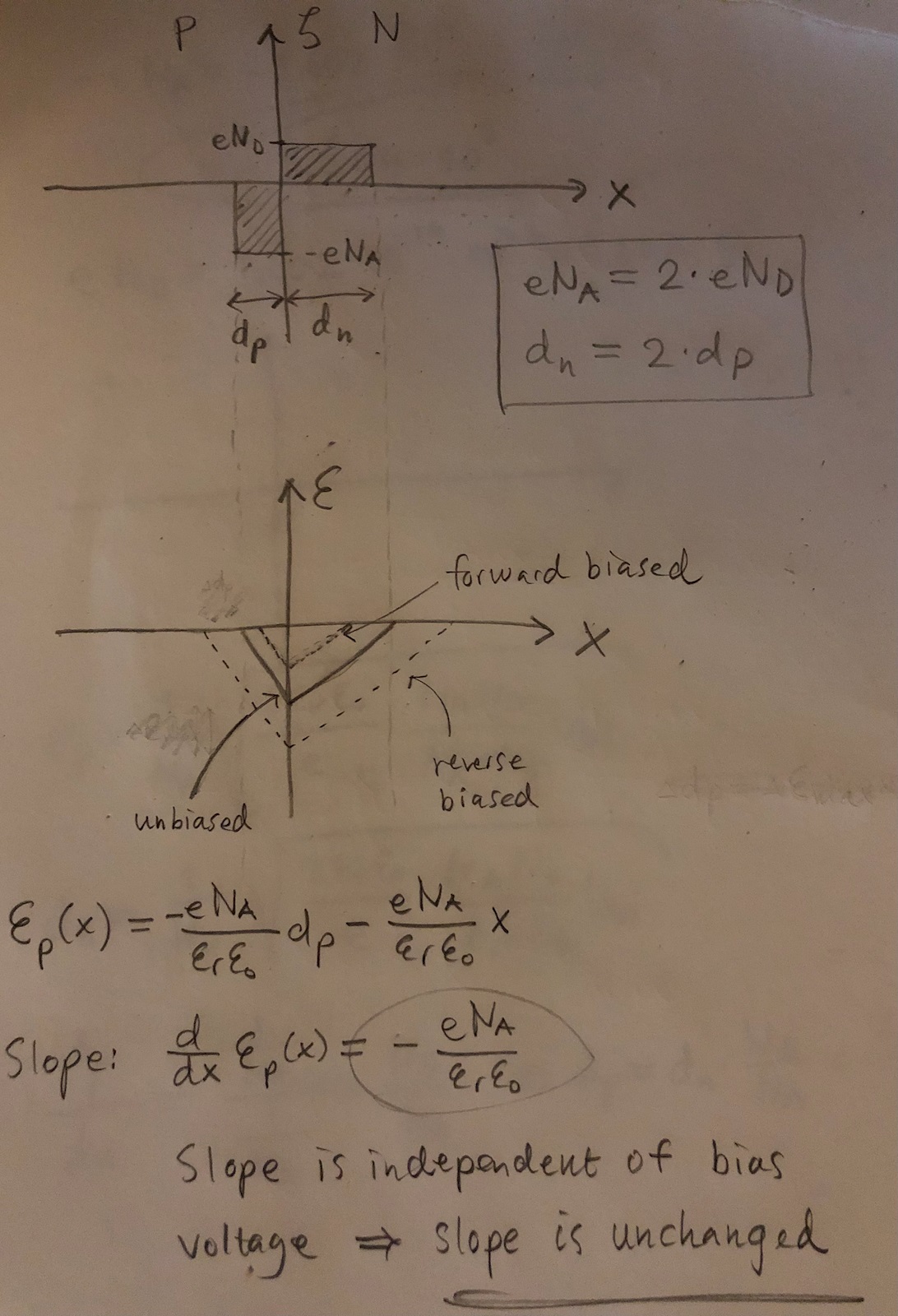
Lite mer detaljerat resonemang. $N_{A} = 2 \cdot 10^{22}, N_{D} = 10^{22}$

jonnefcb skrev:
En lärare gav mig feedback som fick mig att tvivla på mitt resonemang.

Vad sade läraren då?

Det är ju känt att utarmningskiktets bredd är proportionell mot roten ur spänningen.

Vad sade läraren då?

Hon vill att jag ska rita om och förklara vad som händer med lutningen.

Det är ju känt att utarmningskiktets bredd är proportionell mot roten ur spänningen.

Ja men det borde väl inte spela någon roll? Hur utarmningsområdet än ändras så ändras ju E_max proportionellt mot det.

Om man tittar på P-sidan: Linjen skär dessa punkter (-dp, 0) och (0, -E_max).

Lutningen är $\frac{Δ ε}{Δ x} = \frac{- ε_{m a x} - 0}{0 - (d_{p})} = \frac{- ε_{m a x}}{d_{p}} = \frac{- C \cdot d_{p}}{d_{p}} = - C$

där C är en konstant. För varje steg som dp utökas, så ökar triangelns spets med C gånger dp:s ökning. Jag förstår inte hur lutningen skulle kunna ändras utan att ändra dopkoncentrationerna.

Konstig kommentar från läraren.

Det jag försökte säga är att trianglarna är likformiga. Dess area är integralen av fältet, alltså spänningen över den, och den ökar men bredden i kvadrat. Det är ett känt resultat.

Pieter Kuiper skrev:
Det jag försökte säga är att trianglarna är likformiga.

Okej, vad bra. Tack!

Svara

Visa senaste svar