halveringstid
Den 1 januari 2000 placerades 80 mg av ett radioaktivt ämne i en mätstation. Mängden y mg avtar med tiden t år. Halveringstiden är 25år. Bestäm y (t) och rita grafen för åren 2000-2100.
Jag tänkte det vore lämpligt att få ut en funktion först så jag gjorde såhär:
80
och därför blir uttrycket
är detta rätt?
för i facit står det
y (t) = 80 * 0,5t/25
= 80 * 2-t/25
= 80 e-ln 2 * t /25
men jag tycker min metod också är rätt? om inte - kan ni förklara varför?
Hej!
Förutom din avrundning av x är funktionerna identiska, prova rita upp dem i Geogebra. Facits svar är en form av sönderfallslagen (fysik 1) och det är nog därför de svarat på den formen. Om du istället för att ha löst ut x hade fortsatt förenkla och sedan använt identiteten som de gör i facit hade du fått samma svar. Det vill säga, du har påbörjat lösningen som facit har, men istället gjort avrundningen av x. Din metod är inte fel, men avrundningen gör att funktionerna inte längre blir identiska.
goofyahh skrev:Hej!
Förutom din avrundning av x är funktionerna identiska, prova rita upp dem i Geogebra. Facits svar är en form av sönderfallslagen (fysik 1) och det är nog därför de svarat på den formen. Om du istället för att ha löst ut x hade fortsatt förenkla och sedan använt identiteten som de gör i facit hade du fått samma svar. Det vill säga, du har påbörjat lösningen som facit har, men istället gjort avrundningen av x. Din metod är inte fel, men avrundningen gör att funktionerna inte längre blir identiska.
om jag hade gjort som min metod på ett nationellt prov, hade jag fått full port på mitt uttryck? eller hade det blivit poäng avdrag?
sen fattar jag inte riktigt vad som sker här
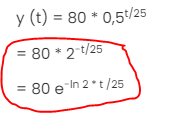
varifrån kommer tvåan och minustecknet från?
Minustecknet kommer av att (1/2)k = 2-k
Sedan har man använt den vanliga omskrivningen att 2 = eln(2) därför att man ofta vill använda naturliga logaritmer i exponentiella funktioner.
Bubo skrev:Minustecknet kommer av att (1/2)k = 2-k
Sedan har man använt den vanliga omskrivningen att 2 = eln(2) därför att man ofta vill använda naturliga logaritmer i exponentiella funktioner.
aha man har alltså "vänt" på talet och utnyttjat att 1/2 = 0,5 och fått minustecken därifrån genom att höja upp tvåan?
men varför kan man inte bara direkt skriva
80 * eln 0,5 * t/25
blir det fel?
naturnatur1 skrev:Bubo skrev:Minustecknet kommer av att (1/2)k = 2-k
Sedan har man använt den vanliga omskrivningen att 2 = eln(2) därför att man ofta vill använda naturliga logaritmer i exponentiella funktioner.
aha man har alltså "vänt" på talet och utnyttjat att 1/2 = 0,5 och fått minustecken därifrån genom att höja upp tvåan?
Just det. Rätt.
men varför kan man inte bara direkt skriva
80 * eln 0,5 * t/25
blir det fel?
Nej, det blir inte fel. Man brukar tycka att det ser snyggare ut med heltal. Hellre -ln(2) än ln(0.5)
Bubo skrev:naturnatur1 skrev:Bubo skrev:Minustecknet kommer av att (1/2)k = 2-k
Sedan har man använt den vanliga omskrivningen att 2 = eln(2) därför att man ofta vill använda naturliga logaritmer i exponentiella funktioner.
aha man har alltså "vänt" på talet och utnyttjat att 1/2 = 0,5 och fått minustecken därifrån genom att höja upp tvåan?
Just det. Rätt.
men varför kan man inte bara direkt skriva
80 * eln 0,5 * t/25
blir det fel?
Nej, det blir inte fel. Man brukar tycka att det ser snyggare ut med heltal. Hellre -ln(2) än ln(0.5)
tack snälla för hjälpen


