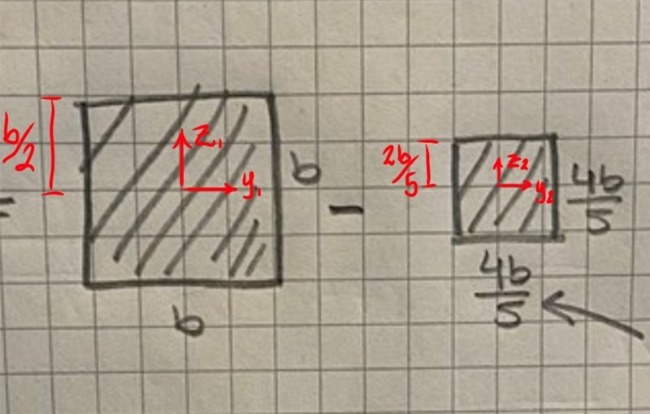
Hållfasthetslära tvärsnitt


 1) varför får jag 0,49 istället för 0,59?
1) varför får jag 0,49 istället för 0,59?
2) hur ska man tolka att viktminskningen blir 49% utifrån ekvationen ovan? Alltså från b=a/(0,59)^1/3
Man kan inte räkna på böjmotstånd sådär, dvs räkna böjmotståndet för en hel kvadrat och sedan dra av böjmotståndet för den inre kvadraten.
Truppeduppe skrev:Man kan inte räkna på böjmotstånd sådär, dvs räkna böjmotståndet för en hel kvadrat och sedan dra av böjmotståndet för den inre kvadraten.
Aha okej, det var min lärare som sa att jag skulle testa det när jag frågade om hjälp.
hur ska man göra?
Ett sätt att räkna ut böjmotståndet W är ett dividera tröghetsmomentet I med avståndet från tvärsnittets tyngdpunkten till "kanten" på tvärsnittet. Den punkten på tvärsnittets kant som ligger allra längst bort från tyngdpunkten, i z eller y-led, beroende på vilken axel man utgår från. I ekvationsform för z-led:
Alternativt kolla i ett formelblad hur man räknar ut böjmotståndet för ett rektangulärt ihåligt tvärsnitt då det är ett ganska vanligt tvärsnitt.
Maja9999 skrev:Truppeduppe skrev:Man kan inte räkna på böjmotstånd sådär, dvs räkna böjmotståndet för en hel kvadrat och sedan dra av böjmotståndet för den inre kvadraten.
Aha okej, det var min lärare som sa att jag skulle testa det när jag frågade om hjälp.
hur ska man göra?
Eftersom tvärsnitten är symmetriska runt neutraplanet går det absolut att göra som du gjort och som din lärare säger. Böjmostånden (och tröghetsmomenten) är additiva när de har samma tyngdpunkt. Om de inte har det så får man använda Steiners sats men det är inte krångligare, bara ett steg till.
Jag kan inte se att du gjort fel någonstans. Du räknar ut att b = 1.27a och om du använder det för att räkna ut arean i andra fallet uttryckt i a så får du
Stoppa in b uttryckt i a
dvs arean minskar till 0.58 av vad den ursprungligen var, dvs en minskning med 42%.
Du ska nog ta en diskussion med läraren om läroboken är rätt. Du har i a f förstått det rätt.
CurtJ skrev:Maja9999 skrev:Truppeduppe skrev:Man kan inte räkna på böjmotstånd sådär, dvs räkna böjmotståndet för en hel kvadrat och sedan dra av böjmotståndet för den inre kvadraten.
Aha okej, det var min lärare som sa att jag skulle testa det när jag frågade om hjälp.
hur ska man göra?
Eftersom tvärsnitten är symmetriska runt neutraplanet går det absolut att göra som du gjort och som din lärare säger. Böjmostånden (och tröghetsmomenten) är additiva när de har samma tyngdpunkt. Om de inte har det så får man använda Steiners sats men det är inte krångligare, bara ett steg till.
Jag kan inte se att du gjort fel någonstans. Du räknar ut att b = 1.27a och om du använder det för att räkna ut arean i andra fallet uttryckt i a så får du
Stoppa in b uttryckt i a
dvs arean minskar till 0.58 av vad den ursprungligen var, dvs en minskning med 42%.
Du ska nog ta en diskussion med läraren om läroboken är rätt. Du har i a f förstått det rätt.
Aha aaa okej! Tack
Truppeduppe skrev:Ett sätt att räkna ut böjmotståndet W är ett dividera tröghetsmomentet I med avståndet från tvärsnittets tyngdpunkten till "kanten" på tvärsnittet. Den punkten på tvärsnittets kant som ligger allra längst bort från tyngdpunkten, i z eller y-led, beroende på vilken axel man utgår från. I ekvationsform för z-led:
Alternativt kolla i ett formelblad hur man räknar ut böjmotståndet för ett rektangulärt ihåligt tvärsnitt då det är ett ganska vanligt tvärsnitt.
Tack!!
CurtJ skrev:Maja9999 skrev:Truppeduppe skrev:Man kan inte räkna på böjmotstånd sådär, dvs räkna böjmotståndet för en hel kvadrat och sedan dra av böjmotståndet för den inre kvadraten.
Aha okej, det var min lärare som sa att jag skulle testa det när jag frågade om hjälp.
hur ska man göra?
Eftersom tvärsnitten är symmetriska runt neutraplanet går det absolut att göra som du gjort och som din lärare säger. Böjmostånden (och tröghetsmomenten) är additiva när de har samma tyngdpunkt. Om de inte har det så får man använda Steiners sats men det är inte krångligare, bara ett steg till.
Jag kan inte se att du gjort fel någonstans. Du räknar ut att b = 1.27a och om du använder det för att räkna ut arean i andra fallet uttryckt i a så får du
Stoppa in b uttryckt i a
dvs arean minskar till 0.58 av vad den ursprungligen var, dvs en minskning med 42%.
Du ska nog ta en diskussion med läraren om läroboken är rätt. Du har i a f förstått det rätt.
"Eftersom tvärsnitten är symmetriska runt neutraplanet går det absolut att göra som du gjort och som din lärare säger. Böjmostånden (och tröghetsmomenten) är additiva när de har samma tyngdpunkt"
NEJ. Det är inte rätt att säga att böjmotstånd och tröghetsmoment är additiva även för dubbelsymmetriska tvärsnitt. Varken böjmotstånd eller tröghetsmoment är linjära egenskaper.
Om man räknar på att böjmotstånd skulle vara additiv så får man följande:
Men kolla på formeln för böjmotstånd för ihåligt rektangulärt tvärsnitt i valfri formelblad, exempelvis denna: https://www.structuralbasics.com/section-modulus/, så får man istället:
Dvs, i stället lite mer än om man räknar additivt. Fundera på varför det blir lite mer (kan det ha något att göra med Steiners sats kanske?).
Då får man:
Dvs, tvärsnittets area minskar med 49%. Vid typisk förenkling, att man antar homogen balk med konstant tvärsnitt så leder det också till en viktminskning på 49%.
Truppeduppe skrev:CurtJ skrev:Maja9999 skrev:Truppeduppe skrev:Man kan inte räkna på böjmotstånd sådär, dvs räkna böjmotståndet för en hel kvadrat och sedan dra av böjmotståndet för den inre kvadraten.
Aha okej, det var min lärare som sa att jag skulle testa det när jag frågade om hjälp.
hur ska man göra?
Eftersom tvärsnitten är symmetriska runt neutraplanet går det absolut att göra som du gjort och som din lärare säger. Böjmostånden (och tröghetsmomenten) är additiva när de har samma tyngdpunkt. Om de inte har det så får man använda Steiners sats men det är inte krångligare, bara ett steg till.
Jag kan inte se att du gjort fel någonstans. Du räknar ut att b = 1.27a och om du använder det för att räkna ut arean i andra fallet uttryckt i a så får du
Stoppa in b uttryckt i a
dvs arean minskar till 0.58 av vad den ursprungligen var, dvs en minskning med 42%.
Du ska nog ta en diskussion med läraren om läroboken är rätt. Du har i a f förstått det rätt.
"Eftersom tvärsnitten är symmetriska runt neutraplanet går det absolut att göra som du gjort och som din lärare säger. Böjmostånden (och tröghetsmomenten) är additiva när de har samma tyngdpunkt"
NEJ. Det är inte rätt att säga att böjmotstånd och tröghetsmoment är additiva även för dubbelsymmetriska tvärsnitt. Varken böjmotstånd eller tröghetsmoment är linjära egenskaper.
Om man räknar på att böjmotstånd skulle vara additiv så får man följande:
Men kolla på formeln för böjmotstånd för ihåligt rektangulärt tvärsnitt i valfri formelblad, exempelvis denna: https://www.structuralbasics.com/section-modulus/, så får man istället:
Dvs, i stället lite mer än om man räknar additivt. Fundera på varför det blir lite mer (kan det ha något att göra med Steiners sats kanske?).
Då får man:
Dvs, tvärsnittets area minskar med 49%. Vid typisk förenkling, att man antar homogen balk med konstant tvärsnitt så leder det också till en viktminskning på 49%.
Truppeduppe har rätt och fel. Tröghetsmoment är additativt för samma koordinatsystem. Det har inget med symmetri att göra, det är en ren geometrisk egenskap. Vad Truppeduppe menar med linjära egenskaper förstår jag inte. Är det möjligen exponenten i uttrycket för tröghetsmoment hen avser?
Det innebär, i det här fallet, att du kan räkna ut tröghetsmomentet för H-kvadraten och dra bort tröghetsmomentet för h-kvadraten och få tröghetsmomentet för "lådgränssnittet".
Men Truppeduppe har rätt i din beräkning och där missade jag och det beror på att det summerade tröghetsmomentet ska divideras med avståndet till det fiber som är längst bort från neutrallagret, i det här fallet H/2, för att få snittets böjmotstånd. Dvs tröghetsmomentet är additativt, böjmotståndet är det inte.
Jag hoppas det gör det hela tydligare för frågeställaren annars kan jag utveckla det utifrån tröghetsmomentets definition.
Märk alltså väl:
Yttröghetsmoment är additiva men inte böjmotstånd.
Du kan ändå utnyttja att yttröghetsmoment är additiva men du bör vara försiktig och helst räkna ut yttröghetsmomentet först. Sedan ges böjmotståndet av:
Där är avståndet till yttersta fibern där maximal böjspänning uppstår.
Detta betyder att du från yttröghetsmoment för ett stort massivt kvadratiskt och ett mindre massivt kvadratiskt tvärsnitt kan beräkna böjmotståndet som:
Där är avståndet från tyngdpunkten till yttersta fibern för det resulterande tvärsnittet.
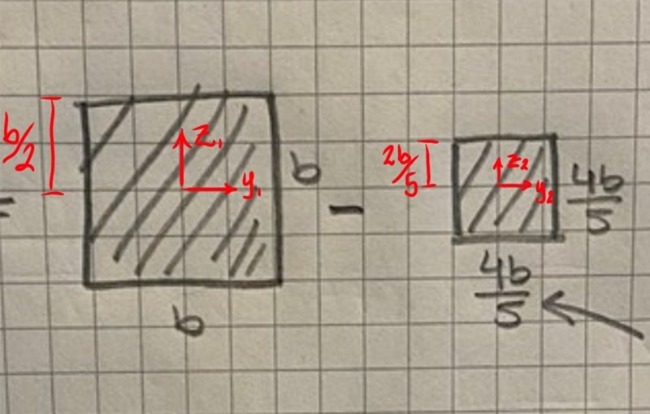
Du ser nu kanske också varför böjmotstånd inte är additiva. Det är nämligen olika avstånd till yttersta fibern för det stora och det mindre tvärsnittet - b/2 respektive 2b/5:
SaintVenant skrev:Märk alltså väl:
Yttröghetsmoment är additiva men inte böjmotstånd.
Du kan ändå utnyttja att yttröghetsmoment är additiva men du bör vara försiktig och helst räkna ut yttröghetsmomentet först. Sedan ges böjmotståndet av:
Där är avståndet till yttersta fibern där maximal böjspänning uppstår.
Detta betyder att du från yttröghetsmoment för ett stort massivt kvadratiskt och ett mindre massivt kvadratiskt tvärsnitt kan beräkna böjmotståndet som:
Där är avståndet från tyngdpunkten till yttersta fibern för det resulterande tvärsnittet.
Du ser nu kanske också varför böjmotstånd inte är additiva. Det är nämligen olika avstånd till yttersta fibern för det stora och det mindre tvärsnittet - b/2 respektive 2b/5:
Ahhhh tack!!
Maja9999 skrev:Ahhhh tack!!
Tacka helst de andra två, jag summerade bara för överblickens skull.