Hållfasthetslära randvillkor

 Får inte med ”EI” någonstans eftersom det kan förkortas bort när HL = 0. Men i svaret ska det finnas med. Hur går jag med det?
Får inte med ”EI” någonstans eftersom det kan förkortas bort när HL = 0. Men i svaret ska det finnas med. Hur går jag med det?
Det är något fel på någon eller några av dina randvillkor och "Får inte med EI någonstans" är en konsekvens av att du tvingar snittstorheter till noll. Det du förutsäger med de randvillkor du valt är att du varken har tvärkrafter eller böjmoment, någonstans i balken, vilket inte är rimligt.
Varför väljer du randvillkoren ?
Du vet definitivt att men detta kan inte uppfyllas av resulterande ansatsen förutom av den triviala lösningen .
Jag föreslår att du ställer upp en lista med lämpliga randvillkor.
Vad säger facit?
SaintVenant skrev:Det är något fel på någon eller några av dina randvillkor och "Får inte med EI någonstans" är en konsekvens av att du tvingar snittstorheter till noll. Det du förutsäger med de randvillkor du valt är att du varken har tvärkrafter eller böjmoment, någonstans i balken, vilket inte är rimligt.
Varför väljer du randvillkoren ?
Du vet definitivt att men detta kan inte uppfyllas av resulterande ansatsen förutom av den triviala lösningen .
Jag föreslår att du ställer upp en lista med lämpliga randvillkor.
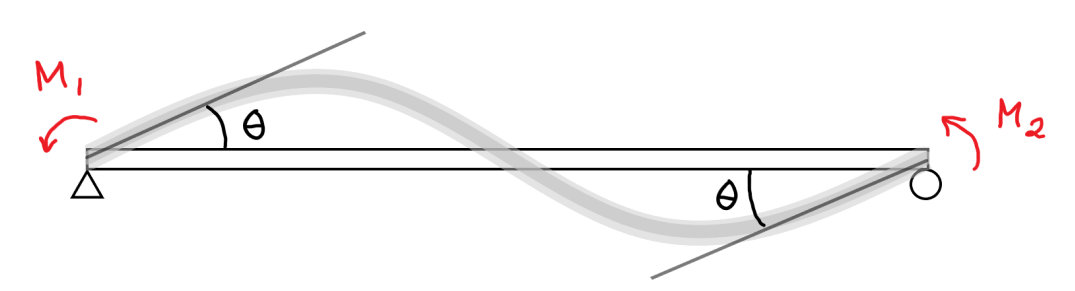
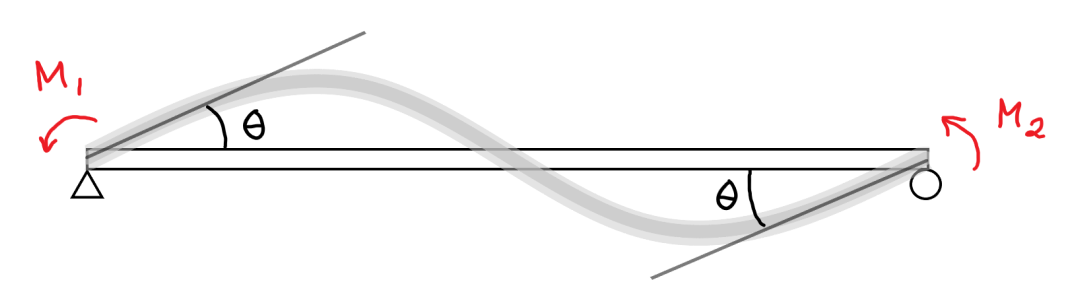
Men är inte momentet 0 vid ett sånt stöd som bilden visar?
Maja9999 skrev:Men är inte momentet 0 vid ett sånt stöd som bilden visar?
Nej. Ett vanligt missförstånd.
Ett sådant stöd kan inte uppta moment. Alltså, du kan inte få ett reaktionsmoment på en yttre last från stödet.
Men, du kan anbringa ett moment på balken vid stödet. Eftersom du föreskriver en vinkeländring vid stödet måste det uppstå moment i balken där.
Försök jämföra med något i verkligheten, så kanske du förstår. Till exempel ett gångjärn, eller liknande.
SaintVenant skrev:Maja9999 skrev:Men är inte momentet 0 vid ett sånt stöd som bilden visar?
Nej. Ett vanligt missförstånd.
Ett sådant stöd kan inte uppta moment. Alltså, du kan inte få ett reaktionsmoment på en yttre last från stödet.
Men, du kan anbringa ett moment på balken vid stödet. Eftersom du föreskriver en vinkeländring vid stödet måste det uppstå moment i balken där.
Försök jämföra med något i verkligheten, så kanske du förstår. Till exempel ett gångjärn, eller liknande.
Hmm jag förstår inte riktigt. Här står det ju att w’’=0 alltså M=0

Förlåt, men läs och begrunda igen.
SaintVenant skrev:Ett sådant stöd kan inte uppta moment. Alltså, du kan inte få ett reaktionsmoment på en yttre last från stödet.
Men, du kan anbringa ett [yttre] moment på balken vid stödet [...]
SaintVenant skrev:Förlåt, men läs och begrunda igen.
SaintVenant skrev:Ett sådant stöd kan inte uppta moment. Alltså, du kan inte få ett reaktionsmoment på en yttre last från stödet.
Men, du kan anbringa ett [yttre] moment på balken vid stödet [...]
Hmmmmm men är det bara i denna uppgift det finns ett moment där? Eftersom det finns en föreskriven vinkeländring?
För jag tänker på bilden jag skickade, där står det ju att randvillkoret för ett sånt stöd är att M ska vara lika med noll?
Maja9999 skrev:Hmmmmm men är det bara i denna uppgift det finns ett moment där? Eftersom det finns en föreskriven vinkeländring?
För jag tänker på bilden jag skickade, där står det ju att randvillkoret för ett sånt stöd är att M ska vara lika med noll?
Det uppstår ett böjmoment inuti balken där, för att du har en föreskriven vinkeländring, ja. Det är faktiskt synonymt med att du vrider med ett moment vid och av en viss storlek och detta producerar samma resultat.
Det är alltså ekvivalent med följande:
Två yttre moment och ger upphov till vinkeländringar vid stöden.
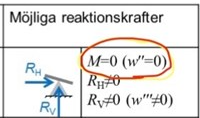
Notera sedan vad som står i din bild:
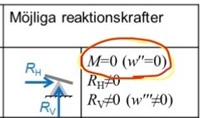
Alltså, möjliga reaktionslaster vid stödet är enbart vertikala och horisontella krafter, ej moment. Men vi talar inte om reaktionsmoment här. Detta handlar om när du har en yttre last, så som en kraft eller ett moment. Då kan inte stödet ge upphov till något reaktionsmoment. På samma sätt som att ett rullstöd med hjul inte kan ge upphov till någon horisontell kraft.
Men, det kan fortfarande uppstå horisontella normalkrafter vid stödet där om du t.ex. föreskriver en styrd förskjutning:

Det uppstår alltså en horisontell normalkraft i punkten trots att det finns en glidled. Det subtila här är att det inte är på grund av stödet utan inuti balken, egentligen. Men matematiskt är detta en och samma punkt, eftersom det är ett endimensionellt objekt vi analyserar i modellen. Se nedan:

Här står det att men, återigen, vi får en horisontell kraft vid stödet inuti balken på grund av den föreskrivna förskjutningen .
SaintVenant skrev:Maja9999 skrev:Hmmmmm men är det bara i denna uppgift det finns ett moment där? Eftersom det finns en föreskriven vinkeländring?
För jag tänker på bilden jag skickade, där står det ju att randvillkoret för ett sånt stöd är att M ska vara lika med noll?
Det uppstår ett böjmoment inuti balken där, för att du har en föreskriven vinkeländring, ja. Det är faktiskt synonymt med att du vrider med ett moment vid och av en viss storlek och detta producerar samma resultat.
Det är alltså ekvivalent med följande:
Två yttre moment och ger upphov till vinkeländringar vid stöden.
Notera sedan vad som står i din bild:
Alltså, möjliga reaktionslaster vid stödet är enbart vertikala och horisontella krafter, ej moment. Men vi talar inte om reaktionsmoment här. Detta handlar om när du har en yttre last, så som en kraft eller ett moment. Då kan inte stödet ge upphov till något reaktionsmoment. På samma sätt som att ett rullstöd med hjul inte kan ge upphov till någon horisontell kraft.
Men, det kan fortfarande uppstå horisontella normalkrafter vid stödet där om du t.ex. föreskriver en styrd förskjutning:
Det uppstår alltså en horisontell normalkraft i punkten trots att det finns en glidled. Det subtila här är att det inte är på grund av stödet utan inuti balken, egentligen. Men matematiskt är detta en och samma punkt, eftersom det är ett endimensionellt objekt vi analyserar i modellen. Se nedan:
Här står det att men, återigen, vi får en horisontell kraft vid stödet inuti balken på grund av den föreskrivna förskjutningen .
Oj tack så jättemycket! Tror jag förstår nu:
så om vi har något föreskrivet i uppgiften, kommer det göra att vi får ett inre moment/kraft beroende på vad. Och denna hamnar på stödet trots att det inte är en reaktionskraft/moment utan en inre kraft?
en fråga bara. denna inre kraft/moment, har det något med snittkraften/momenten att göra? Är det samma sak?
 vad gjorde jag för fel nu då istället? Är inte w(0)=0 heller?
vad gjorde jag för fel nu då istället? Är inte w(0)=0 heller?
Maja9999 skrev:Oj tack så jättemycket! Tror jag förstår nu:
så om vi har något föreskrivet i uppgiften, kommer det göra att vi får ett inre moment/kraft beroende på vad. Och denna hamnar på stödet trots att det inte är en reaktionskraft/moment utan en inre kraft?
Japp.
en fråga bara. denna inre kraft/moment, har det något med snittkraften/momenten att göra? Är det samma sak?
Exakt samma sak. De är snittstorheter som uppstår inuti balken.
Maja9999 skrev:vad gjorde jag för fel nu då istället? Är inte w(0)=0 heller?
Du har inte gjort något fel, vad jag kan se. Tvärtom har du förstått ursprungliga problemet väldigt väl. Du behöver bara en till ekvation, ett till randvillkor. Du har nämligen introducerat en okänd som behöver tas om hand med en ekvation.
Vilket randvillkor saknas?
SaintVenant skrev:Maja9999 skrev:Oj tack så jättemycket! Tror jag förstår nu:
så om vi har något föreskrivet i uppgiften, kommer det göra att vi får ett inre moment/kraft beroende på vad. Och denna hamnar på stödet trots att det inte är en reaktionskraft/moment utan en inre kraft?
Japp.
en fråga bara. denna inre kraft/moment, har det något med snittkraften/momenten att göra? Är det samma sak?
Exakt samma sak. De är snittstorheter som uppstår inuti balken.
Aaa okej tack!
SaintVenant skrev:Maja9999 skrev:vad gjorde jag för fel nu då istället? Är inte w(0)=0 heller?
Du har inte gjort något fel, vad jag kan se. Tvärtom har du förstått ursprungliga problemet väldigt väl. Du behöver bara en till ekvation, ett till randvillkor. Du har nämligen introducerat en okänd som behöver tas om hand med en ekvation.
Vilket randvillkor saknas?
Oj jag vet inte?
Maja9999 skrev:Oj jag vet inte?
Du har nu använt fyra, men du har också introducerat ännu en okänd i form av , du behöver därmed använda ett till Randvillkor. Vad är nedböjningen vid till exempel? Eller vinkeln vid ?
Sedan kan jag påpeka att momentet inte ska ha olika tecken, de har ju samma riktning.
SaintVenant skrev:Maja9999 skrev:Oj jag vet inte?
Du har nu använt fyra, men du har också introducerat ännu en okänd i form av , du behöver därmed använda ett till Randvillkor. Vad är nedböjningen vid till exempel? Eller vinkeln vid ?
Aha okej så man ska sätta in tex w(L)=0 då eller? Eller är nedböjningen 0 där?
Sedan kan jag påpeka att momentet inte ska ha olika tecken, de har ju samma riktning.
Men blir det inte olika tecken om man snittar sådär som jag gjorde?
Maja9999 skrev:Men blir det inte olika tecken om man snittar sådär som jag gjorde?
Jo, helt rätt, det är en negativ snittyta. Mitt misstag. Det blir fel annars såg jag nu.
Aha okej så man ska sätta in tex w(L)=0 då eller? Eller är nedböjningen 0 där?
Japp, det är ett stöd där.
SaintVenant skrev:Maja9999 skrev:Men blir det inte olika tecken om man snittar sådär som jag gjorde?
Jo, helt rätt, det är en negativ snittyta. Mitt misstag. Det blir fel annars såg jag nu.
Aha okej så man ska sätta in tex w(L)=0 då eller? Eller är nedböjningen 0 där?
Japp, det är ett stöd där.
Yes okej tack!!
Så, det enda problemet med lösningsmetoden är att du inför detta moment men det kan i lösningen vara ganska oklart var det kommer ifrån. Speciellt eftersom det inte är ett yttre moment i problemet, även om du får samma svar och det blir ett ekvivalent problem.
Det är ett problem för att jag vet att vissa föreläsare kan vara ganska stela och rigida i sina tankesätt, så då kan man få avdrag för principiella fel om man ställer upp ett alternativt men ekvivalent problem. För att "Det är inte problemet du skulle lösa". Alltså, att man måste skriva någon långrandig motivation för varför de är ekvivalenta.
Därmed tycker jag du också ska pröva att lösa uppgiften utan att introducera med randvillkoren:
SaintVenant skrev:Så, det enda problemet med lösningsmetoden är att du inför detta moment men det kan i lösningen vara ganska oklart var det kommer ifrån. Speciellt eftersom det inte är ett yttre moment i problemet, även om du får samma svar och det blir ett ekvivalent problem.
Det enda jag vet är att vissa föreläsare kan vara ganska stela och rigida i sina tankesätt, så då kan man få avdrag för principiella fel om man ställer upp ett alternativt men ekvivalent problem. För att "Det är inte problemet du skulle lösa". Alltså, att man måste skriva någon långrandig motivation för varför de är ekvivalenta.
Därmed tycker jag du också ska pröva att lösa uppgiften utan att introducera med randvillkoren:
Ahaa yes okej. Jag testade det från en början men det var då jag inte fick med ”EI” termen i w(x) funktionen, men den kanske inte ska vara med här? (Dock satte jag inte ena vinkeln till negativ, så ska testa igen!)
Maja9999 skrev:Ahaa yes okej. Jag testade det från en början men det var då jag inte fick med ”EI” termen i w(x) funktionen, men den kanske inte ska vara med här? (Dock satte jag inte ena vinkeln till negativ, så ska testa igen!)
Naej. Då satte du väl?
Maja9999 skrev:(Dock satte jag inte ena vinkeln till negativ, så ska testa igen!)
Det där med tecknet på lutningen kan faktiskt vara fel av mig. För egentligen är väl vinkeländringen i punkten i samma riktning. Om man tänker utifrån ett positivt snitt sett...
Jag är ute och flänger så jag kan inte riktigt grotta ned mig i det men jag kan återkomma ikväll om du inte listar ut det.
SaintVenant skrev:Maja9999 skrev:(Dock satte jag inte ena vinkeln till negativ, så ska testa igen!)
Det där med tecknet på lutningen kan faktiskt vara fel av mig. För egentligen är väl vinkeländringen i punkten i samma riktning. Om man tänker utifrån ett positivt snitt sett...
Jag är ute och flänger så jag kan inte riktigt grotta ned mig i det men jag kan återkomma ikväll om du inte listar ut det.
Yes ingen fara. Tack för hjälpen! Ska försöka igen
SaintVenant skrev:Maja9999 skrev:(Dock satte jag inte ena vinkeln till negativ, så ska testa igen!)
Det där med tecknet på lutningen kan faktiskt vara fel av mig. För egentligen är väl vinkeländringen i punkten i samma riktning. Om man tänker utifrån ett positivt snitt sett...
Jag är ute och flänger så jag kan inte riktigt grotta ned mig i det men jag kan återkomma ikväll om du inte listar ut det.
Om du får tid över hade du jättegärna fått kolla på denna tråden också. Hade varit supersnällt! För jag förstod när du förklarar.
https://www.pluggakuten.se/trad/elementarfall-hallfasthetslara/
Vad blev w(x) till slut i din första uppgift?