Hållfasthetslära förlängning av stav
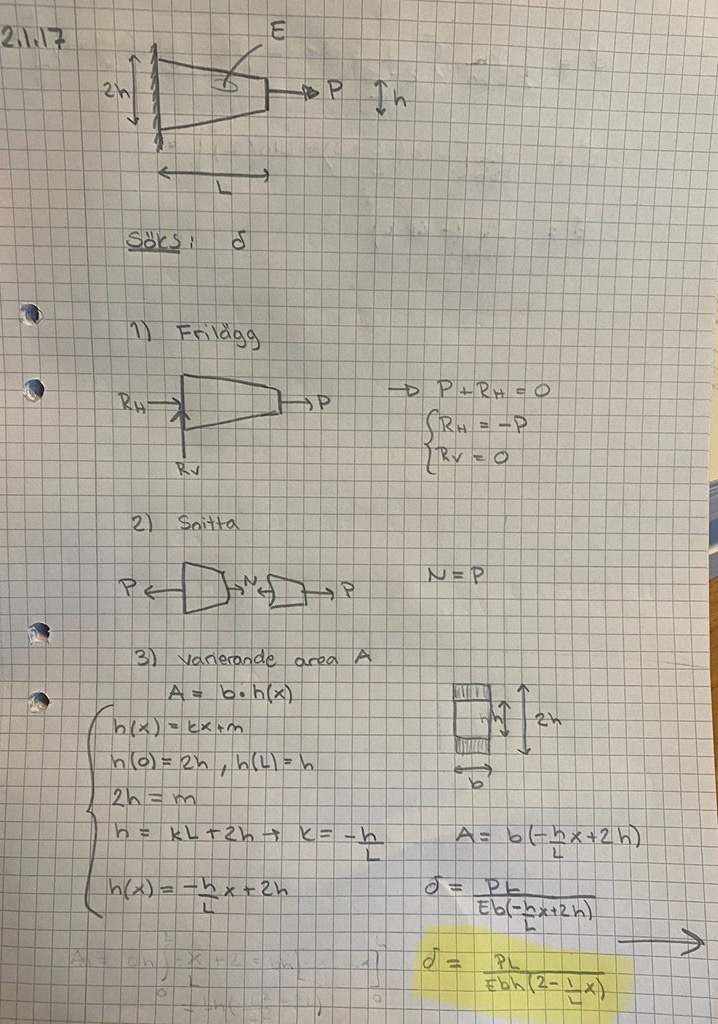
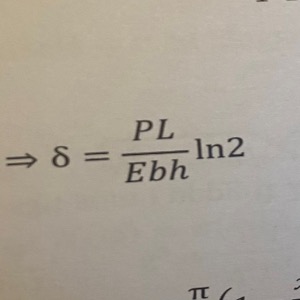Hur får jag mitt svar (gulmarkerat) till detdär? Antar att man ska ta en integral över något? Men hur, varför?
Eftersom arean är variabel så kan du inte använda uttrycket för delta som det är men tänk såhär:
Snitta en tunn skiva, dx tjock, och beskriv arean för den som en funktion av x. På den tunna skivan kan du använda uttrycket för delta om vi antar att skivans area är konstant för den och det kan vi om dess tjocklek är infitesimal. När du räknat ut delta för den skivan så kan du göra likadant för alla skivor i stångens längsled, dvs för 0<= x <= L och det gör du, som du misstänkt, genom att integrera uttrycket för delta över x-intervallet. Integrationen är ju bara en summering över ett jättestort (oändligt) antal skivor med jätteliten (oändligt liten) tjocklek.
Får du ihop det?
