3
svar
179
visningar
teknikomatte behöver inte mer hjälp
Hållf, potentiella energins minimum för att bestämma utböjning av balk
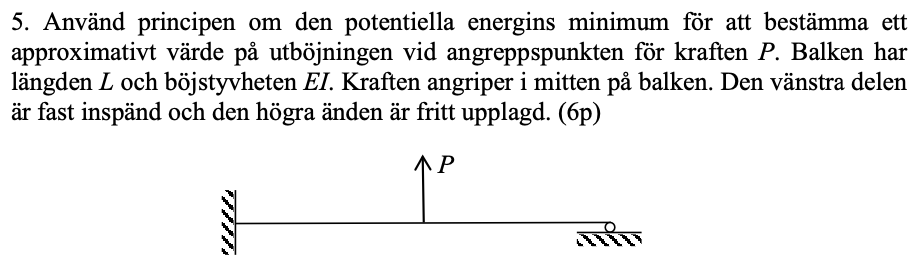

Jag har gjort på samma sätt som facit, men jag gjorde ansatsen och får därför ett svar som skiljer sig från facit, varför kan man inte göra den ansatsen, den uppfyller ju randvillkoren?
Derivera ditt uttryck och stoppa in x=0. Det blir inte 0.
Calle_K skrev:Derivera ditt uttryck och stoppa in x=0. Det blir inte 0.
Hmm sant, kollade snabbt och såg inte att derivatan ska vara noll. Men varför ska den vara det? Jag försökte lösa uppgiften genom att tillämpa samma logik som de gjort på uppgiften nedan, och där har de inte ett krav på att derivatan ska vara 0, och därför gjort samma ansats.
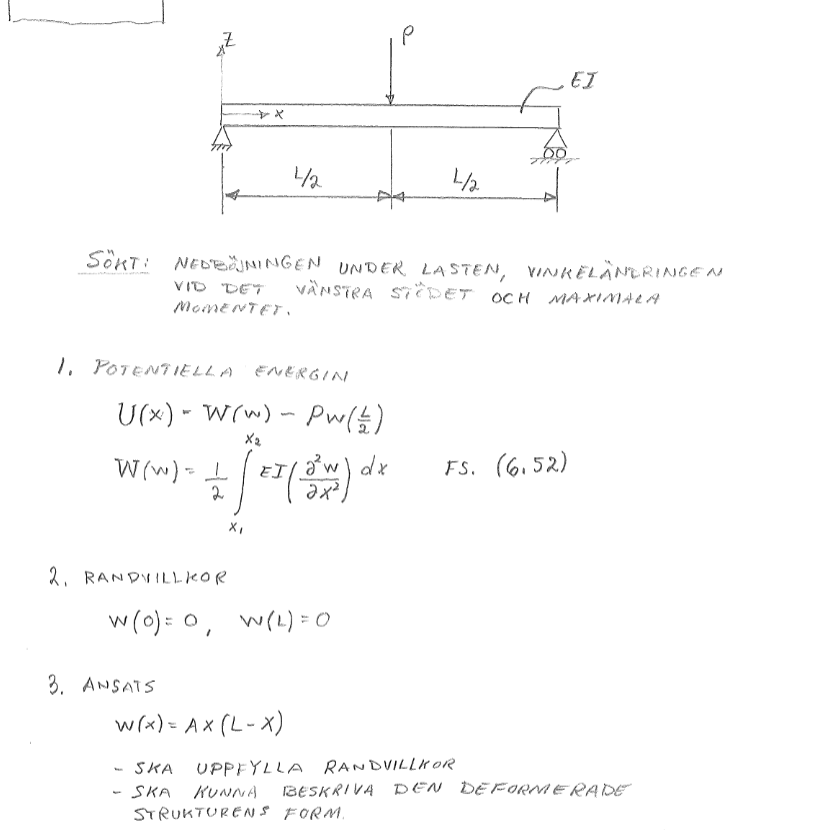
Nevermind, förstår varför. Den sitter fast i väggen och därför måste derivatan också vara 0.


