Hållf-förskjutningar, stänger

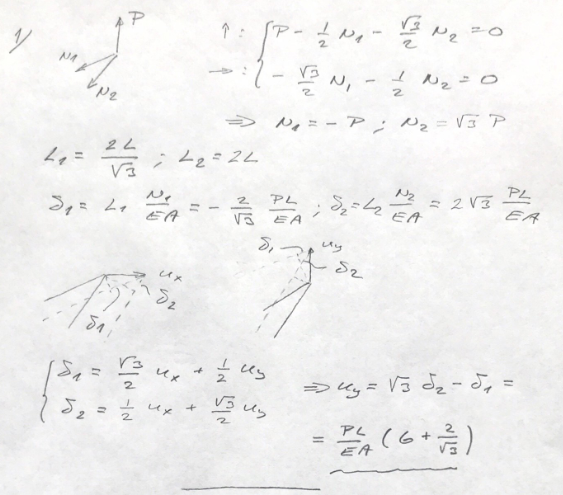
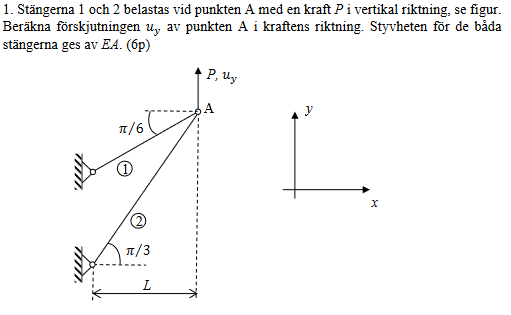Vad är det som sker under materialsambanden delta_1 och delta_2 i facit? (Alltså i deformationsfigurerna) Man har ansatt ett u_x och u_y som ser ut att vara projektioner av delta_1 samt delta_2 men delta_1 och delta_2 är också linjärkombinationer av u_x och u_x? Hur kommer det sig? Detta sker konsekvent i liknande uppgifter och jag förstår inte riktigt tankesättet.

Mvh

Man beräknar hur mycket stängerna förlängs om man förskjuter noden A ett litet stycke u = (u_x, u_y). Man antar att förskjutningen u är liten så att man kan anse att förlängningen är linjär i u och behandlar u_x och u_y separat och superponerar resultaten.

Tillägg: 20 aug 2024 00:50

Har du möjlighet att utveckla på hur superponeringen fungerar? På bilderna ser det ut som att du har fått två ekvationer för delta*L så ätt man kan uttrycka u_x i u_y.

istället ska man alltså addera dessa?

Ja, precis, för små u så kan vi kolla hur mycket förlängningen blir för en förskjutning i horisontell led och hur mycket förlängningen blir för en förskjutning i vertikal led och addera resultaten för att få förlängningen då vi har förskjutning i båda led samtidigt. Men det fungerar bara om u är litet.

Om ni har gått igenom Maclaurinutvecklingen så kan man se det som

$δ L (u_{x}, u_{y}) =$ $= δ L (0, 0) + \frac{\partial δ L}{\partial u_{x}} (0, 0) \cdot u_{x} + \frac{\partial δ L}{\partial u_{y}} (0, 0) \cdot u_{y} + O ({|(u_{x}, u_{y})|}^{2}) = \frac{\partial δ L}{\partial u_{x}} (0, 0) \cdot u_{x} + \frac{\partial δ L}{\partial u_{y}} (0, 0) \cdot u_{y} + O ({|(u_{x}, u_{y})|}^{2})$ .

Där vi anser att förskjutningar är små om de är så små att resttermen $O ({|(u_{x}, u_{y})|}^{2})$ kan försummas, och vi får ett linjärt uttryck för förlängningen.

Jag har för alla praktiska skäl förstått hur du menar att man ska göra (villket egentligen räcker för tentan), men känner mig lite trög så har en till fråga om detaljerna;

På bilderna du skickade så ansätter man ett U=(u_x, u_y) och sedan tar man fram ett uttryck för delta*L. Detta gör man för bägge riktning (x och y) och sedan så adderar man resultaten varur man har ett uttryck för delta*L med kompnenter i relevanta riktningar.

Det som fortfarande förvirrar är hur detta är förenligt med att man ansätter samma $δ L = u_{y} \sin α = u_{x} \cos α = u_{y} \sin α + u_{x} \cos α$ ?

Nja, det är olika $δ L$ . Kanske skulle jag kalla dem $δ L_{x}$ och $δ L_{y}$ .

$δ L = δ L_{x} + δ L_{y}$ .

Men så har man inte gjort i facit.

Okej tack så mycket. Då förstår jag

Svara

Visa senaste svar