Hållf elementarfall moment
Hej, jag har följande uppgift och facit:
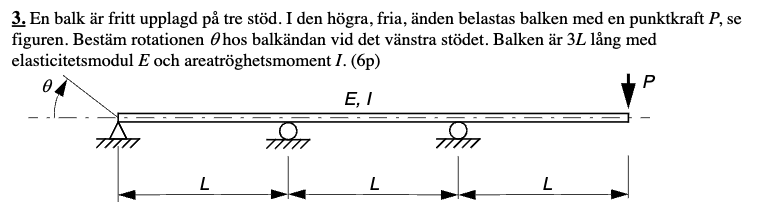
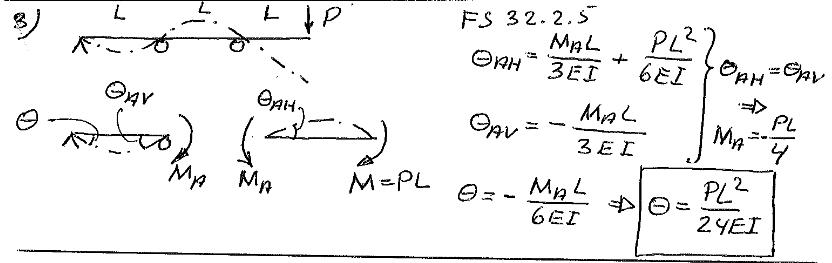
Hur kommer det sig att ? Om ,
borde inte , då avståndet bara är 2L istället för L, från kraften P?
Och varför är momenten 0 längst till vänster?
Det är bättre om du försöker lösa problemet på ett eget sätt än att försöka tyda facit. Detta för att de hoppar över redovisning av ganska många steg och det verkar finnas vissa luckor i din kunskap.
Tips: Använd elementarfall (vilket/vilka?)
Frågor:
- Är detta problem statiskt bestämt eller obestämt? Varför?
- Om du snittar och tar fram snittstorheter någonstans i intervallet 0<x<L, vad får du för uttryck för moment och tvärkraft?
- Om du tar bort mellersta stödet vid x=L från vänstra sidan, kan du lösa problemet då? Kan du försöka lösa det med elementarfall?
Finns det inte en allmän lösningsgång som man borde kunna följa?
Har inte pluggat sen ja skrev inlägget men tänkte börja nu igen. Jag förstår nu varför momentet MA inte är 2PL, pga reaktionskrafterna väl, och att momentet är 0 längst till vänster har väl att göra med själva figuren för stödet, som visar att det är 0?
Absolut, det finns en allmän lösningsgång. Men lösningsförslaget följer inte denna då det hoppar över hälften av alla steg. Detta för att det förväntas att den som tar del av förslaget redan känner till lösningsgången i stora drag.
Jag förstår nu varför momentet MA inte är 2PL, pga reaktionskrafterna väl...
Ja, det kan man säga.
...att momentet är 0 längst till vänster har väl att göra med själva figuren för stödet, som visar att det är 0
Ett ledat stöd kan inte uppta moment i punkten och därmed genereras inga reaktionsmoment. Anledningen till att snittmomentet är noll där är för att det är slutet på balken.
Om du vill ha hjälp att lösa uppgiften kan du börja med att studera och svara på mina frågor i inlägg #2, så kan vi ta det därifrån.
Om du vill ha hjälp att lösa uppgiften kan du börja med att studera och svara på mina frågor i inlägg #2, så kan vi ta det därifrån.
Jag gör det lite senare ikväll, tack!
Skulle det vara möjligt att även gå igenom den allmänna lösningsgången för elementarfall uppgifter?
teknikomatte skrev:Skulle det vara möjligt att även gå igenom den allmänna lösningsgången för elementarfall uppgifter?
Det är vad vi kommer göra. Men du kommer få jobba lite för det. Vill du ha en lösningsgång serverad finns det på YouTube eller i många andra trådar här på PA.
SaintVenant skrev:
- Är detta problem statiskt bestämt eller obestämt? Varför?
- Om du snittar och tar fram snittstorheter någonstans i intervallet 0<x<L, vad får du för uttryck för moment och tvärkraft?
- Om du tar bort mellersta stödet vid x=L från vänstra sidan, kan du lösa problemet då? Kan du försöka lösa det med elementarfall?
1. Statiskt obestämt då om vi ställer upp kraft och momentjämvikt så har vi fler okända än ekvationer, dvs vi måste hitta fler ekvationer med elementarfall.
2. Förstår inte riktigt, moment och tvärkraft är väl olika beroende på vart man snittar.
3. Man kan ju ersätta det med en kraft men ser inte hur man skulle kunna lösa det utan att dela upp det i elementarfall precis som de gjort i facit
teknikomatte skrev:
1. Statiskt obestämt då om vi ställer upp kraft och momentjämvikt så har vi fler okända än ekvationer, dvs vi måste hitta fler ekvationer med elementarfall.
Japp, vilket är en hint till svaret på 3.
2. Förstår inte riktigt, moment och tvärkraft är väl olika beroende på vart man snittar.
Ja, men du kan alltid snitta och ta fram ett uttryck som gäller över ett intervall. I detta fall efterfrågade jag ett som är giltigt för . Speciellt så att du kan svara på din egen fråga:
"Och varför är momenten 0 längst till vänster?"
Om vi kallar stödet längst till vänster för punkt A, får vi ett uttryck enligt:
Du ser då snabbt att momentet är noll längst till vänster.
3. Man kan ju ersätta det med en kraft men ser inte hur man skulle kunna lösa det utan att dela upp det i elementarfall precis som de gjort i facit
Om du helt tar bort stödet i mitten är problemet ej längre statiskt obestämt. Men, det kan vara en bra övning att försöka lösa det med elementarfall för att förstå proceduren.
Första steget för din uppgift
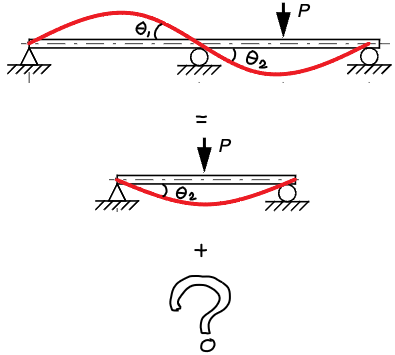
I en typisk formelsamling finns inte elementarfall för en balk där en del hänger utanför, de har alltid stöd i ändarna eller är fast inspända. Alltså vill vi omformulera till ett annat men ekvivalent problem.
Vet du hur du kan göra det?
Exempelproblem
Skulle du kunnat lösa uppgiften om den såg ut som nedan istället?
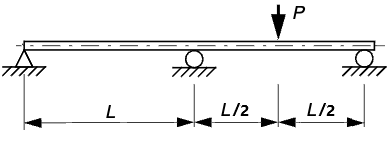
Vi ser att den är statiskt obestämd för att vi har tre stöd. Ett sätt att lösa den på är med elementarfall. Idén då är att formulera en jämviktsekvation från elementarfall. Detta kan vi få från att vi vet två saker om stödet i mitten:
Fundera själv först på om du vet något "tvång" för stödet i mitten, klicka sedan här
- Vinkeln är samma till vänster som till höger
- Deformationen är noll
Detta kan illustreras med en deformationsbild:
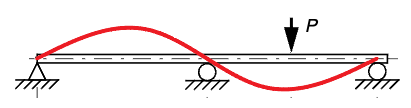
Vi kan välja två olika sätt för att få fram ett extra samband:
1.
Först formulerar vi elementarfall för den högra delen av balken och den vänstra delen av balken. Där vinkeln i ändarna de möts ska vara lika: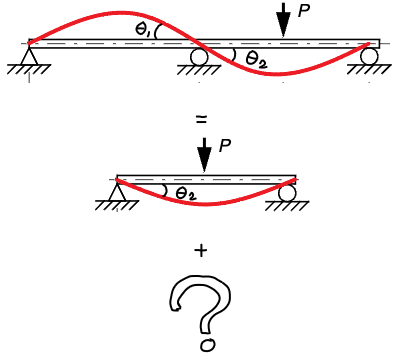
Alltså, att . Hur ska elementarfallet för den vänstra balken se ut?
2.
Eller så kan vi formulera ett elementarfall där vi har kraften P nedåt och ett där vi har reaktionskraften uppåt:
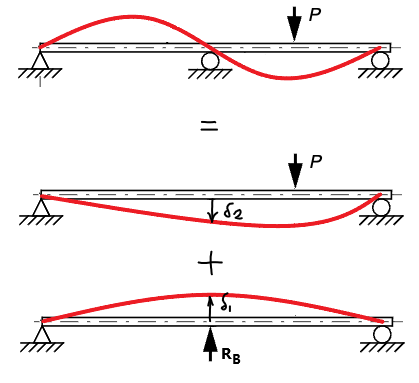
Hur skulle tvånget vi har mellan deformationerna och se ut matematiskt?
Sambandet blir ...
... inget svårare än .
OBS: Här visar jag exempel på hur man kan göra för att formulera ett tredje samband så att man kan ta fram uttryck för alla okända i problemet. I din uppgift söker man vinkeln i vänstra änden och då är inte alla lösningar likvärdiga i termer av tidsåtgång.
Tack för ditt utförliga svar! Förstår bättre nu men har en sak som jag inte riktigt förstår.
Om vi kallar stödet längst till vänster för punkt A, får vi ett uttryck enligt:
Du ser då snabbt att momentet är noll längst till vänster.
Hmm men om man istället hade att det hade varit fast inspänt istället för stödet längst till vänster, hade momentet fortfarande blivit 0? Anledningen till att jag frågor är pga att i en annan uppgift där balken är fast inspänd i randen så är momentet ej 0, varför?
Försökte dessutom lösa uppgiften på mitt egna sätt. Kom såhär långt
Men förstår ej hur jag ska få fram , nu vet jag att det ska bli PL men hur vet jag ej. Tänkte lösa uppgiften på så sätt att jag får fram alla obekanta, känns bra som träning att göra det.
Hmm men om man istället hade att det hade varit fast inspänt istället för stödet längst till vänster, hade momentet fortfarande blivit 0? Anledningen till att jag frågor är pga att i en annan uppgift där balken är fast inspänd i randen så är momentet ej 0, varför?
Ett fast inspänt randvillkor kan ta upp moment och krafter i båda led. Alltså, motsätter sig randvillkoret rotation av balken i punkten. Om du jämför med att något är fastsvetsat så förstår du nog mekaniken bakom.
Ett ledat stöd kan inte ta upp något moment. Det är alltså som en led vilken balken kan rotera fritt kring. Detta betyder inte automatiskt att momentet inuti balken är noll i punkten där det finns ett ledat stöd. Detta eftersom det internt i balken kan uppstå motstånd mot fri rotation. Alltså interna moment. Mellan lager av balken.
Men, i slutet av balken, för det sista snittet längst ut, finns det inget motstånd och det kan rotera fritt. Då blir det interna momentet i ett "tänkt snitt" noll. Jämför med om du inte hade haft något ledat stöd, om den är fritt hängande. Då hade också momentet varit noll.
Varför är detta viktigt
Problemet med att associera de där stöden direkt med att momentet är noll är att man kan lura sig att de innebär att momentet ska vara noll även om det inte är slutet av balken.
Men förstår ej hur jag ska få fram , nu vet jag att det ska bli PL men hur vet jag ej.
Det är PL för att kraften i änden anbringar momentet gånger sin hävarm . Istället för att rita dit symbolen för fast inspänning på vänstersidan kan du där rita in vertikala kraften och momentet .
SaintVenant skrev:Hmm men om man istället hade att det hade varit fast inspänt istället för stödet längst till vänster, hade momentet fortfarande blivit 0? Anledningen till att jag frågor är pga att i en annan uppgift där balken är fast inspänd i randen så är momentet ej 0, varför?
Ett fast inspänt randvillkor kan ta upp moment och krafter i båda led. Alltså, motsätter sig randvillkoret rotation av balken i punkten. Om du jämför med att något är fastsvetsat så förstår du nog mekaniken bakom.
Ett ledat stöd kan inte ta upp något moment. Det är alltså som en led vilken balken kan rotera fritt kring. Detta betyder inte automatiskt att momentet inuti balken är noll i punkten där det finns ett ledat stöd. Detta eftersom det internt i balken kan uppstå motstånd mot fri rotation. Alltså interna moment. Mellan lager av balken.
Men, i slutet av balken, för det sista snittet längst ut, finns det inget motstånd och det kan rotera fritt. Då blir det interna momentet i ett "tänkt snitt" noll. Jämför med om du inte hade haft något ledat stöd, om den är fritt hängande. Då hade också momentet varit noll.
Okej, så om jag förstått dig rätt. Moment kommer endast att vara skiljt från noll i randen när vi har en fast inspänning. Om vi har att balken är på stöd / hänger fritt så kommer momentet vara noll i randen, men däremot så kan det finnas moment skiljt från noll om det finns stöd som inte är på randen.
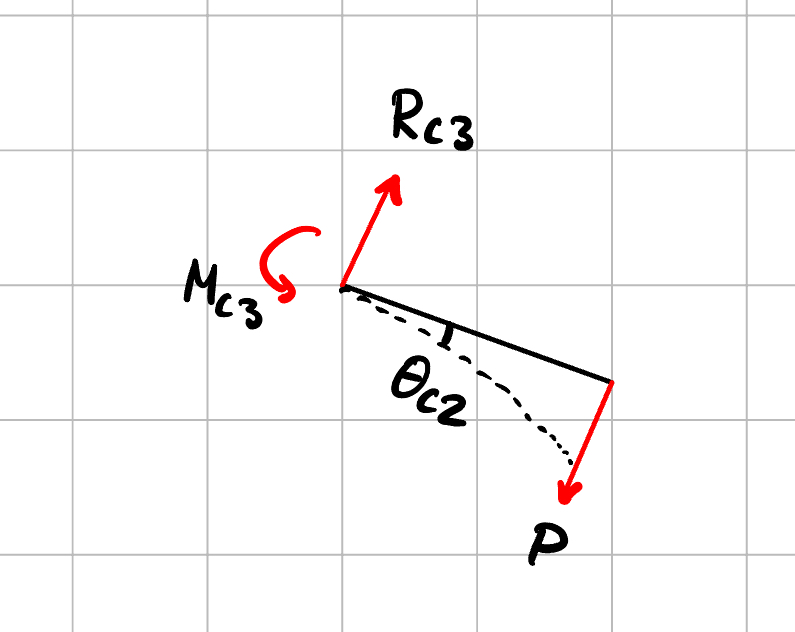
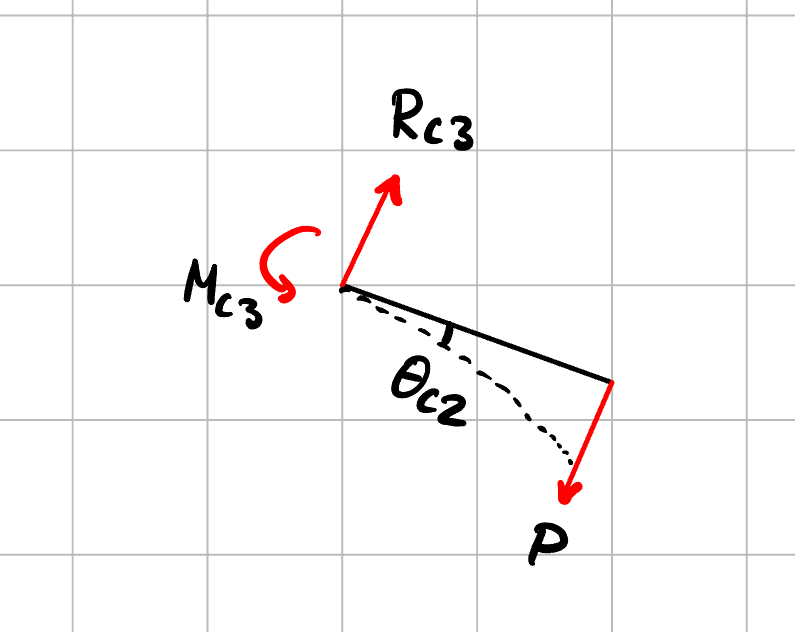
Istället för att rita dit symbolen för fast inspänning på vänstersidan kan du där rita in vertikala kraften Rc3R_{c3} och momentet Mc3=Mc2M_{c3}=M_{c2}.
Menar du såhär?`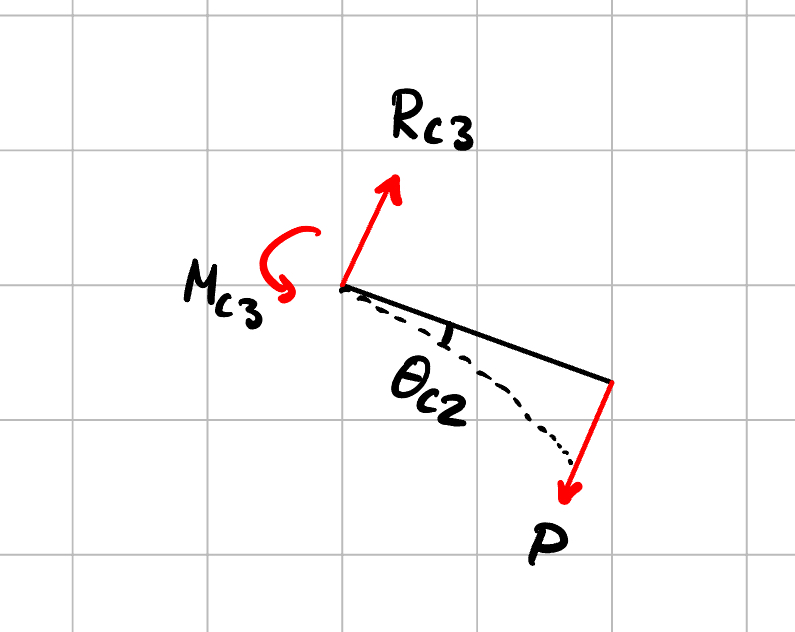
Men jag tror jag har gjort fel med vinkeln, för visst stämmer det inte att vinkeln som jag har ritat är samma som vinkeln i det mittersta elementarfallet?
I en typisk formelsamling finns inte elementarfall för en balk där en del hänger utanför, de har alltid stöd i ändarna eller är fast inspända. Alltså vill vi omformulera till ett annat men ekvivalent problem.
Vet du hur du kan göra det?
Jag antar att man gör det på samma sätt som jag gjort i inlägg #10, dvs ersätter det med en fast inspänning som är vinklad?
Först formulerar vi elementarfall för den högra delen av balken och den vänstra delen av balken. Där vinkeln i ändarna de möts ska vara lika:
Alltså, att . Hur ska elementarfallet för den vänstra balken se ut?
Hmm, varför har du ersatt det mittersta stödet med "triangelstödet"?
Väldigt bra! Du har ställt många bra frågor som jag tyvärr inte haft tid att svara ordentligt på.
teknikomatte skrev:Hmm, varför har du ersatt det mittersta stödet med "triangelstödet"?
Denna kan jag svara snabbt på.
Det är för att en balk måste ha ett rullande stöd om inte det ska uppstå normalkrafter i balkens riktning. Annars kommer böjningen leda till icke försumbar krökning och sedermera dragning i längsriktningen.
Detta betyder med andra ord att triangelstöd och rullstöd på ena eller andra sidan är ekvivalent. Så länge som den fritt upplagda balken har båda. Det blir ingen skillnad på resultatet för vinkel, reaktionskraft eller nedböjning.
Väldigt bra! Du har ställt många bra frågor som jag tyvärr inte haft tid att svara ordentligt på.
Ingen fara, uppskattar hjälpen jag får!
Denna kan jag svara snabbt på.
Det är för att en balk måste ha ett rullande stöd om inte det ska uppstå normalkrafter i balkens riktning. Annars kommer böjningen leda till icke försumbar krökning och sedermera dragning i längsriktningen.
Detta betyder med andra ord att triangelstöd och rullstöd på ena eller andra sidan är ekvivalent. Så länge som den fritt upplagda balken har båda. Det blir ingen skillnad på resultatet för vinkel, reaktionskraft eller nedböjning.
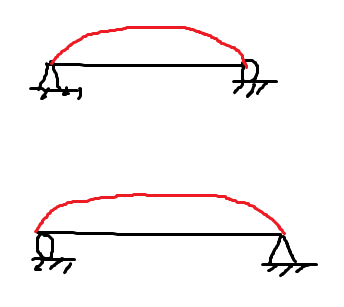
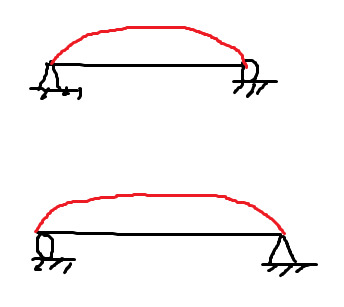
Då antar jag att det du markerat med frågetecken ska vara någon av följande: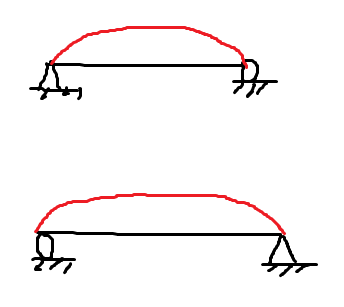
Gissningsvis så är det endast den översta som fungerar, då det känns logiskt att randen till vänstermåste vara densamma för att bibehålla ursprungsproblemet, men anledningen till att jag la in båda är för du skrev att triangelstöd och rullstöd på ena eller andra sidan är ekvivalent.
En till grej: Hur ska man veta sånthär? Jag pluggar nämligen inför en Fx komplettering för denna kursen (balkböjning och spänningstillstånd är det som kommer på kompletteringen, men det är balkböjning jag har svårt för) som gick under hela våren på KTH, jag gick på föreläsningar och övningar som handlade om elementarfall men det är ju så mycket detaljer och saker som jag inte hade någon aning om, sen får man ju inte upp något om man försöker hitta på Google heller. Går det att lösa samma uppgifter med exempelvis elastiska linjens ekvation? Då jag känner att det är extremt krångligt och kreativitet som krävs för att lösa uppgifterna med elementarfall.
Vill du ha en lösningsgång serverad finns det på YouTube eller i många andra trådar här på PA.
Hur hittar jag den? haha, har letat men hittar inget
En sak jag kan säga är att alla dessa detaljer kommer från matematiken hos randvillkoren. Med utgångspunkt i elastiska linjens ekvation kan du beskriva randvillkoren och dess konsekvenser för nedböjning, vinkel, moment och tvärkrafter.
Du kan lösa alla problem med elastiska linjens ekvation om du använder Heaviside step-funktioner och Dirac delta. Eller kombinerade s.k. Macaulay-funktioner. Det finns vissa specialfall som inte går att lösa och så klart problem som faller utanför de antaganden som gäller för differentialekvationen. Men de kommer oftast inte i en grundläggande hållf-kurs.
Några tips
Jag vet inte när kompletteringen är och hur mycket tid du har men det finns några saker jag kan tipsa om. Det första är att jag tycker svensk undervisning i grundläggande hållf och svensk litteratur för hållfasthetslära generellt är ganska dålig. Speciellt på KTH om man läser teknisk fysik. Undervisningen innehåller där väldigt få detaljer och hoppar över det mesta. För att få mer kött på benen bör du leta efter amerikansk College / University litteratur. Det finns många som är bra och många som är tillgängliga online.
Speciellt om du söker på Solid Mechanics eller Mechanics of Materials. En jag speciellt tycker är bra är enkelt Hibbelers Mechanics of Materials 8:e eller 9:e utgåva. Ska finnas på KTHs bibliotek i elektroniskt format.
Om du bara är intresserad av balkböjning kan du söka på Beam Solving eller liknande på YouTube. Sedan är också Chat GPT 4o alternativt AnsysGPT väldigt bra på att svara på frågor relaterade till hållfasthetslära, speciellt om du ber dessa utgå från sina källor.
Du kan läsa denna tråd:
https://www.pluggakuten.se/trad/rakna-ut-stodreaktioner-pa-en-balk-med-tre-stod/
Där jag långt ned i inlägg #14 och #15 ger en hel genomgång av olika sätt att göra på för ett långrandigt problem.
teknikomatte skrev:Då antar jag att det du markerat med frågetecken ska vara någon av följande:
Gissningsvis så är det endast den översta som fungerar, då det känns logiskt att randen till vänstermåste vara densamma för att bibehålla ursprungsproblemet, men anledningen till att jag la in båda är för du skrev att triangelstöd och rullstöd på ena eller andra sidan är ekvivalent.
Japp. Men, vilka laster ska vara på den? Är det några yttre moment? Yttre krafter?
teknikomatte skrev:Istället för att rita dit symbolen för fast inspänning på vänstersidan kan du där rita in vertikala kraften och momentet .
Menar du såhär?`
Japp.
Men jag tror jag har gjort fel med vinkeln, för visst stämmer det inte att vinkeln som jag har ritat är samma som vinkeln i det mittersta elementarfallet?
Det som är samma som andra sidan av stödet är hur vinklad den fast inspända balken är vid sin inspänning.
Alltså, så här:

Det innebär att totala vinkeln i högra änden av balken du ritat här är om är vinkeln för den fast inspända balken i sin högra ände.
Tänk på att vinkeln vid randvillkoret fast inspänning är noll. Så som du hade ritat det i figuren ovan är det ganska oklart var vinkeln beräknas. Menade du vid änden på balken? Alltså, approximativt arctan(nedböjning/längd)?
Det bör vara som nedan:

Har för tillfället inte så mycket tid men jag kollar igenom när jag kommer hem och återkommer. Tack igen för dina förklaringar!
teknikomatte skrev:Har för tillfället inte så mycket tid men jag kollar igenom när jag kommer hem och återkommer. Tack igen för dina förklaringar!
Ingen fara. Jag svarar samtidigt som jag gör annat (står i kö på Liseberg) så jag gör många misstag eller vill lägga till saker som jag tycker saknas. Bara bra om du väntar lite med att läsa allt.
SaintVenant skrev:teknikomatte skrev:Då antar jag att det du markerat med frågetecken ska vara någon av följande:
Gissningsvis så är det endast den översta som fungerar, då det känns logiskt att randen till vänstermåste vara densamma för att bibehålla ursprungsproblemet, men anledningen till att jag la in båda är för du skrev att triangelstöd och rullstöd på ena eller andra sidan är ekvivalent.
Japp. Men, vilka laster ska vara på den? Är det några yttre moment? Yttre krafter?
Asså det är väl bara krafterna från stöden och sedan böjmomentet man får när man "delar upp" balken?
Om du bara är intresserad av balkböjning kan du söka på Beam Solving eller liknande på YouTube. Sedan är också Chat GPT 4o alternativt AnsysGPT väldigt bra på att svara på frågor relaterade till hållfasthetslära, speciellt om du ber dessa utgå från sina källor.
Du kan läsa denna tråd:
https://www.pluggakuten.se/trad/rakna-ut-stodreaktioner-pa-en-balk-med-tre-stod/
Där jag långt ned i inlägg #14 och #15 ger en hel genomgång av olika sätt att göra på för ett långrandigt problem.
Precis det är bara balkböjning.
Jag har läst igenom den tråden flera gånger, men jag har väldigt svårt att lösa elementarfall uppgifter när det är en ny "situation" och det känns som att det alltid är olika sätt att lösa uppgiften, dvs att det inte finns en allmänn lösningsgång.
SaintVenant skrev:teknikomatte skrev:Istället för att rita dit symbolen för fast inspänning på vänstersidan kan du där rita in vertikala kraften och momentet .
Menar du såhär?`
Japp.
Men jag tror jag har gjort fel med vinkeln, för visst stämmer det inte att vinkeln som jag har ritat är samma som vinkeln i det mittersta elementarfallet?
Det som är samma som andra sidan av stödet är hur vinklad den fast inspända balken är vid sin inspänning.
Alltså, så här:
Det innebär att totala vinkeln i högra änden av balken du ritat här är om är vinkeln för den fast inspända balken i sin högra ände.
Tänk på att vinkeln vid randvillkoret fast inspänning är noll. Så som du hade ritat det i figuren ovan är det ganska oklart var vinkeln beräknas. Menade du vid änden på balken? Alltså, approximativt arctan(nedböjning/längd)?
Det bör vara som nedan:
Okej, är med på allt tror jag, men varför måste väggen egentligen vara vinklad när man ersätter ursprungsproblemet? Anledningen till att jag gjorde den vinklad är bara för att jag hade sett liknande uppgift tidigare.
Denhär tråden blev väldigt bökig känner jag då det är väldigt mycket olika saker som jag inte förstår och ifrågasätter. Men ska checka källorna du nämnde också för att förhoppningsvis förstå lite bättre. Tycker att allt i hållf kursen var ganska straight forward men just balkböjning var extremt invecklat.
Men har kompletteringen den 21/8 och har kvällar/helger att plugga så förhoppningsvis hinner man bemästra elementarfall