Hallå snälla har matteprov imorn måste få minst ett B

På hur många sätt kan personerna arragnera sig totalt och på hur många sätt kan A och B sitta bredvid varandra? Rita gärna.

Kolla på 8 sätt

Eller nej det står fel på sidan men jag fick att det blev 12 

Jag tycker det är en bra början, som du har gjort, men jag förstår inte riktigt allt. Hur som helst:

Om det finns fem stolar kan A och B sätta sig bredvid varandra på följande antal sätt: 

och så gånger två, eftersom de kan byta plats med varandra också. Totalt finns det alltså 10 sätt de kan sätta sig bredvid varandra. På hur många sätt kan man arrangera fem personer totalt?

Men sista funkar ju inte de ska sitta brevid varandra inte på dedär sätter.

Det är 8 platser inte 10 plus att då är det 3 stolar kvar för de andra bokstäverna

Jo, den sista funkar visst. Om de sitter runt ett bord kommer ytterkanterna vara bredvid varandra också. Om du "böjer" formen så att det blir en cirkel ser du att de hamnar bredvid varandra.

Men hur ska ja veta om de sitter i en cirkel tho, Altså ja förstår vad du menar men Ja om vi har 10 sannolikhet att de sitter brevid varandra ska vi räkna ut då resten? Altså deras sannolikhet är det då 10x3x2 eller jag vet inte

Det står att de sitter runt ett bord. Oavsett om de sitter runt ett cirkulärt bord eller ett rektangulärt bord kommer ytterkanterna hamna bredvid varandra. 

Hur som helst vet vi nu att de kan sitta bredvid varandra på 10 olika sätt. Att arrangera 5 personer kan man göra på $5!=5·4·3·2·1$ sätt eller 120 sätt. Så sannolikheten att de hamnar bredvid varandra blir $\frac{10}{120}=\frac{1}{12}\approx 8.3 \%$.

Va nej i facit står det 40% och de står inte runt ett bord så därför tror jag att det är 8 liksom inte 10 plus att om vi tänker lite på de så är det (5x4x3x2x1) som blir 120 då som du sa så hur funkar det då är det fel igen 

Väldigt märkligt. Antingen missförstår jag frågan då eller så har jag helt enkelt fel, för jag tycker facits svar verkar väldigt konstigt. 

Ursäkta att jag inte kunde vara mer hjälpsam!

Jag förstår det är ok.Men ja Aså ja kopiera frågan från boken så vet faktist inte har försökt hela dagen också

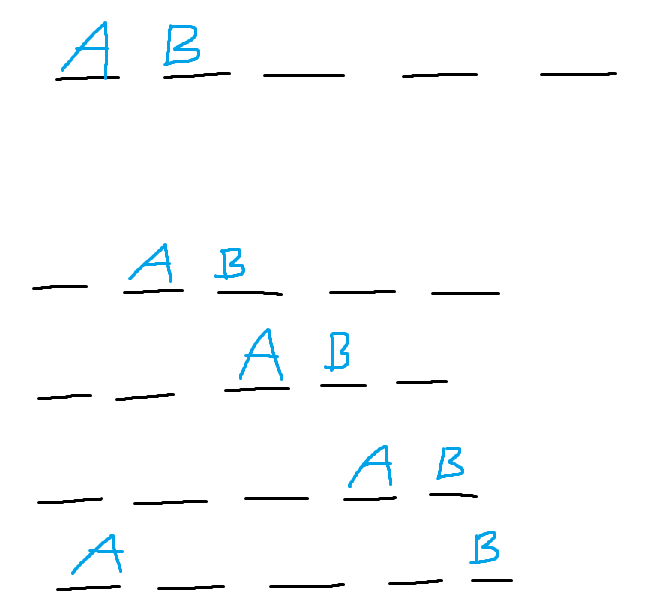
Om du tittar på naytte's bild så har du ABxxx där xxx är CDE som ska placeras och de kan placeras på 3!=6 olika sätt. Det gör att den raden representerar 6 utfall. Det samma gäller rad 2-4 och därmed har du 4*6 sätt att få AB i den ordningen. Sen måste du göra samma sak för BA och det ger dig 24 sätt till dvs totalt 48 kombinationer av de totalt 120 som ni redan kommit fram till. Det blir 40%

Va nej kolla jag löste det

först är det 8 olika sätt man kan välja imellan

sen är det 5 stolar gånger 4 eftersom det är A och B vi räknar så 5x4 är 20 så det blir 8 av 20 som är lika med 40% eftersom vi ska inte räkna alla möjligheter utan bara möjligheterna att till exempel A hamnar i först och B i tredje osv och sånna möjliga är 20

Det är alldeles rätt räknat men du måste nog förklara det bättre på ett prov för att få full pott om din lärare har en dålig dag. 

Om man utgår från formeln för sannolikhet så har vi P = gynsamma utfall/möjliga utfall. Gynsamma är ju 8 som vi kommit fram till och om vi nu sätter A på första stolen så kan B sätta sig på någon av de andra 4, dvs 4 möjliga sätt. Detta upprepas för varje ny position som A sätter sig i så, precis som du säger, så är alla möjliga utfall 4x5=20. 

Bra jobbat!

Hej! Jag är också fast på denna uppgift just nu, hur fick ni till 20? Vad menar ni med 5x4 och vart kommer det ifrån?